Равномерное прямолинейное движение.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: виды механического движения, скорость.
Равномерное прямолинейное движение материальной точки - это движение с постоянной скоростью \(\vec{v}\). Обратите внимание, что речь идёт о постоянстве вектора скорости; это значит, что скорость неизменна как по модулю, так и по направлению.
Траекторией тела при равномерном прямолинейном движении служит прямая (или часть прямой - например, отрезок или луч). Вдоль данной прямой тело движется равномерно, то есть с постоянной по модулю скоростью.
Закон движения.
Предположим, что тело, двигаясь равномерно и прямолинейно со скоростью \(\vec{v}\), переместилось за время \(t\) из точки \(M_{0}\) в точку \(M\) (рис. 1). Вектор перемещения есть \(\vec{s}=\overrightarrow{M_{0}M}\).
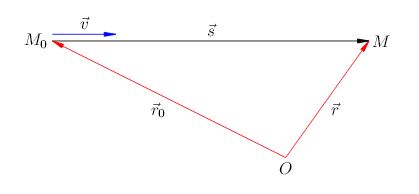 |
| Рис. 1. Равномерное прямолинейное движение |
Путь, пройденный телом, равен длине \(s\) вектора перемещения. Очевидно, что выполнено соотношение:
\(s=vt,\), (1)
где \(v\) - модуль вектора скорости.
Формула (1) справедлива для любого равномерного движения (не обязательно прямолинейного). Но в случае прямолинейного равномерного движения эта формула становится соотношением между векторами. В самом деле, поскольку векторы \(\vec{s}\) и \(\vec{v}\) сонаправлены, формула (1) позволяет записать:
\(\vec{s}=\vec{v}t.\) (2)
Как обычно, движение тела рассматривается в некоторой системе отсчёта, связанной с телом отсчёта \(O\) (рис. (1); координатные оси не изображаем). Пусть \(\vec{r_{0}}\) - радиус-вектор начальной точки \(M_{0}\) и \(\vec{r}\) - радиус-вектор конечной точки \(M\). Тогда, очевидно,
\(\vec{s}=\vec{r}-\vec{r_{0}}\). Подставим эту разность в формулу (2):
\(\vec{r}-\vec{r_{0}}=\vec{v}t\).
Отсюда получаем закон движения, то есть зависимость радиус-вектора тела от времени:
\(\vec{r}=\vec{r_{0}}+\vec{v}t\). (3)
Закон движения решает основную задачу механики, то есть позволяет найти зависимость координат тела от времени. Делается это просто.
Координаты точки \(M_{0}\) обозначим (\(x_{0},y_{0},z_{0}\)). Они же являются координатами вектора \(\vec{r_{0}}\). Координаты точки \(M\) (и вектора \(\vec{r}\)) обозначим \((x, y, z)\). Тогда векторная формула (3) приводит к трём координатным соотношениям:
\(\displaystyle x=\displaystyle x_{0}+\displaystyle v_{\displaystyle x}\displaystyle t,\) (4)
\(y=y_{0}+v_{\displaystyle y}t,\) (5)
\(z=z_{0}+v_{\displaystyle z}t.\) (6)
Формулы (4)-(6) представляют координаты тела как функции времени и потому служат решением основной задачи механики для равномерного прямолинейного движения.
Интегрирование.
Ключевая формула (3), описывающая равномерное прямолинейное движение, может быть получена из несколько иных соображений. Вспомним, что производная радиус-вектора есть скорость точки:
\(\frac{\displaystyle d\vec{r}}{\displaystyle dt}=\vec{v}. \) (7)
В случае равномерного прямолинейного движения имеем \(\vec{v}=const\). Что нужно продифференцировать, чтобы получить постоянный вектор \(\vec{v}\)? Очевидно, функцию \(\vec{v}t\). Но не только: к величине \(\vec{v}t\) можно прибавить любой постоянный вектор \(\vec{c}\) (это не изменит производную, поскольку производная константы равна нулю). Таким образом:
\(\vec{r}=\vec{c}+\vec{v}t. \) (8)
Каков смысл константы \(\vec{c}\)? Если \(t=0\), то радиус-вектор \(\vec{r}\) равен своему начальному значению \(\vec{r_{0}}\). Поэтому, полагая \(t=0\) в формуле (8), получим:
\(\vec{r_{0}}=\vec{c}\).
Итак, вектор \(\vec{c}\) есть начальное значение радиус-вектора, и теперь из (8) мы снова приходим к формуле (3):
\(\vec{r}=\vec{r_{0}}+\vec{v}t\).
Мы, таким образом, проинтегрировали равенство (7) при условии, что \(\vec{v}=const\). Интегрирование - это операция, обратная дифференцированию. Интегрировать в физике приходится на каждом шагу, так что привыкайте :-)

























