Этот метод – настоящий подарок для тех, кто хочет высокие баллы на ЕГЭ. Оказывается, что во многих случаях уравнение с параметром можно просто решить. Так же, как мы решаем обычные уравнения, применяя равносильные преобразования.
Никаких сложностей! Никаких длинных объяснений. Просто действуем по алгоритму.
1. Найдите все значения \(a\), при каждом из которых уравнение
\(\sqrt{3x-2}\cdot ln(x-a)=\sqrt{3x-2}\cdot ln(2x+a)\) имеет ровно один корень на отрезке \([0;1]\).
Решение:
Запишем уравнение в виде:
\(\sqrt{3x-2}\cdot (ln(x-a)-ln(2x+a))=0.\)
Используем аналитический метод. Решим это уравнение. В левой его части произведение множителей, в правой ноль.
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю, а другой при этом имеет смысл. Уравнение равносильно системе:
\(\left\{\begin{matrix}
3x-2\geq 0, \\
x-a>0, \\
2x+a>0, \\
\left[\begin{matrix}
x=\displaystyle \frac{2}{3}, \\
ln(x-a)=ln(2x+a);\end{matrix}\right.\end{matrix}\right.
\Leftrightarrow\)\(\left\{\begin{matrix}
x\geq \displaystyle \frac{2}{3}, \\
x>a, \\
x>-\displaystyle \frac{a}{2}, \\
\left[\begin{matrix}
x=\displaystyle \frac{2}{3}, \\
x-a=2x+a;\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\)\(\left[\begin{matrix}
\left\{\begin{matrix}
x=\displaystyle \frac{2}{3}, \\
x>a, \\
x>-\displaystyle \frac{a}{2},\end{matrix}\right. \\
\left\{\begin{matrix}
x-a=2x+a, \\
x\geq \displaystyle \frac{2}{3}, \\
x>a, \\
x> -\displaystyle \frac{a}{2}.\end{matrix}\right.\end{matrix}\right.\)
Упростим каждую из систем.
Сначала первая система: \(\left\{\begin{matrix}
x=\displaystyle \frac{2}{3}, \\
x>a, \\
x>-\displaystyle \frac{a}{2}.\end{matrix}\right.\)
Подставив \(x=\displaystyle \frac{2}{3}\) в оба неравенства, получим: \(\left\{\begin{matrix}
x=\displaystyle \frac{2}{3}, \\
a<\displaystyle \frac{2}{3}, \\
-\displaystyle \frac{a}{2}<\frac{2}{3};\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
x=\displaystyle \frac{2}{3}, \\
-\displaystyle \frac{4}{3} < a < \frac{2}{3}.\end{matrix}\right.\)
Теперь вторая система: \(\left\{\begin{matrix}
x-a=2x+a, \\
x\geq \displaystyle \frac{2}{3}, \\
x>a, \\
x>-\displaystyle \frac{a}{2}.\end{matrix}\right.\)
Из первого уравнения: \(x=-2a\). Подставив это значение \(x\) во все неравенства, придем к системе:
\(\left\{\begin{matrix}
x=-2a, \\
-2a\geq \displaystyle \frac{2}{3}, \\
-2a>a, \\
-2a>-\displaystyle \frac{a}{2};\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x=-2a, \\
a\leq -\displaystyle \frac{1}{3}.\end{matrix}\right.\)
Таким образом, исходное уравнение равносильно совокупности:
\(\left[\begin{matrix}
\left\{\begin{matrix}
x=\displaystyle \frac{2}{3}, \\
-\displaystyle \frac{4}{3 }< a < \frac{2}{3},\end{matrix}\right. \\
\left\{\begin{matrix}
x=-2a, \\
a\leq -\displaystyle \frac{1}{3}.\end{matrix}\right.\end{matrix}\right.\)
Мы просто решили это уравнение с параметром. Нашли его корни при всех значениях параметра. Мы сказали, что при \(-\displaystyle \frac{4}{3}<a<\frac{2}{3}\) у уравнения есть корень \(x=\displaystyle \frac{2}{3}\), а при \(a\leq -\displaystyle \frac{1}{3}\) еще и корень \(x=-2a\).
Посмотрим, при каких значениях параметра уравнение имеет единственный корень на отрезке \([0; 1]\).
С учетом условия \(x\in [0; 1]\) получаем:
\(\left[\begin{matrix}
\left\{\begin{matrix}
x=\displaystyle \frac{2}{3}, \\
0\leq \displaystyle \frac{2}{3}\leq 1, \\
-\displaystyle \frac{4}{3}< a < \frac{2}{3},\end{matrix}\right. \\
\left\{\begin{matrix}
x=-2a, \\
0\leq -2a\leq 1, \\
a\leq -\displaystyle \frac{1}{3}.\end{matrix}\right.\end{matrix}\right.\)
Упростим вторую систему. Что касается первой, то корень \(x=\displaystyle \frac{2}{3}\) принадлежит отрезку \([0; 1]\). Вот результат:
\(\left[\begin{matrix}
\left\{\begin{matrix}
x=\displaystyle \frac{2}{3}, \\
-\displaystyle \frac{4}{3}< a < \frac{2}{3},\end{matrix}\right. \\
\left\{\begin{matrix}
x=-2a, \\
-\displaystyle \frac{1}{2}\leq a \leq -\frac{1}{3}.\end{matrix}\right.\end{matrix}\right.\)
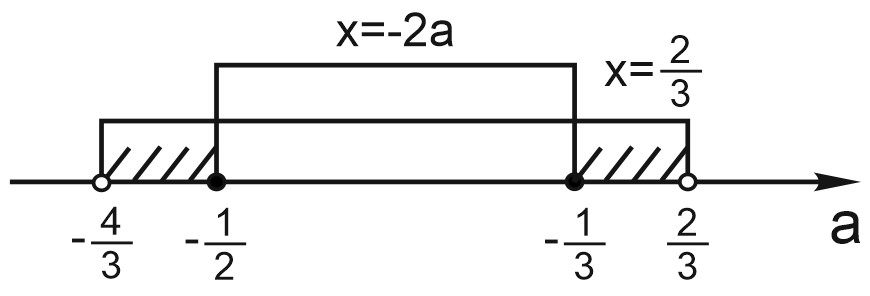
Отметим на оси \(a\) интервалы значений параметра, соответствующих корню \(x=\displaystyle \frac{2}{3}\) и корню \(x=-2a\).
Мы видим, что, если \(-\displaystyle \frac{1}{2}\leq a \leq -\displaystyle \frac{1}{3}\), то уравнение имеет 2 корня на отрезке \([0;1]\) (две «крыши» на рисунке).
Найдем, при каких значениях параметра исходное уравнение имеет ровно один корень на отрезке \([0;1]\).
1) \(-\displaystyle \frac{4}{3}< a < -\frac{1}{2}\) или \(-\displaystyle \frac{1}{3}< a < \frac{2}{3}\) (одна «крыша» на рисунке).
2) Случай совпадения корней, \(-2a=\displaystyle \frac{2}{3}, \; a=-\frac{1}{3}\).
Объединив случаи, запишем ответ: \(a\in \left (-\displaystyle \frac{4}{3};-\frac{1}{2} \right )\cup \left[-\displaystyle \frac{1}{3};\frac{2}{3}\right ).\)
2. При каких значениях параметра \(a\) уравнение \(\sqrt{x-a}\cdot sin x=\sqrt{x-a}\cdot cos x\) имеет ровно один корень на отрезке \([0;\pi]\)?
Решение:
Запишем уравнение в виде \(\sqrt{x-a}\cdot (sin x-cos x)=0\).
Левая часть уравнения равна нулю, если \(x=a\). Или если \(sin x=cos x\), и при этом \(x-a\geq 0\).
Уравнение равносильно совокупности:
\(\left[\begin{matrix}
x=a, \\
\left\{\begin{matrix}
x-a\geq 0, \\
tg x=1;\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix}
x=a, \\
\left\{\begin{matrix}
a\leq x, \\
x=\displaystyle \frac{\pi }{4}+\pi k, \; k\in Z.\end{matrix}\right.\end{matrix}\right.\)
Мы решили это уравнение! Мы сказали, что у него всегда есть корень \(x=a\), и также при условии \(a\leq x\) есть решения \(x=\displaystyle \frac{\pi }{4}+\pi k, \; k\in Z\).
Добавим к совокупности условие \(x\in [0; \pi]\):
\(\left[\begin{matrix}
\left\{\begin{matrix}
x=a, \\
0\leq a\leq \pi, \end{matrix}\right. \\
\left\{\begin{matrix}
x=\displaystyle \frac{\pi }{4}+\pi k, \; k\in Z, \\
0\leq x\leq \pi ,\\
a\leq x.\end{matrix}\right.\end{matrix}\right.\)
Посмотрим на вторую систему. Мы хотим найти корни уравнения \(x=\displaystyle \frac{\pi }{4}+\pi k, \; k\in Z\) на отрезке \([0;\pi]\).
Так же, как в тригонометрических уравнениях в вариантах ЕГЭ с отбором решений на отрезке. Можно сделать это с помощью единичной окружности или двойного неравенства.
На отрезке \([0;\pi]\) лежит только одно решение из серии \(x=\displaystyle \frac{\pi }{4}+\pi k, \; k\in Z\). Это \(x=\displaystyle \frac{\pi }{4}.\)
\(\left[\begin{matrix}
\left\{\begin{matrix}
x=a, \\
0\leq a\leq \pi, \end{matrix}\right. \\
\left\{\begin{matrix}
x=\displaystyle \frac{\pi }{4}, \\
a\leq \displaystyle \frac{\pi }{4}.\end{matrix}\right.\end{matrix}\right.\)
Мы нашли все решения уравнения на отрезке \([0; \pi]\). И узнали, при каких значениях параметра \(a\) существуют эти решения.
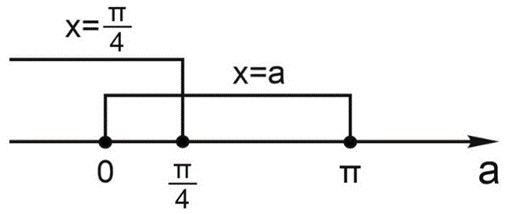
Уравнение имеет ровно одно решение на отрезке \([0;\pi]\) в следующих случаях:
1) \(\left[\begin{matrix}
a < 0, \\
\displaystyle \frac{\pi }{4} < a \leq \pi .\end{matrix}\right.\)
2) Если корни \(x=\displaystyle \frac{\pi }{4}\) и \(x=a\) совпадают, то есть \(a=\displaystyle \frac{\pi }{4}\). Объединив случаи, получаем ответ:
Ответ: \(a\in (-\infty;0 )\cup \left [ \displaystyle\frac{\pi }{4}; \pi \right ].\)
3. При каких значениях параметра \(a\) уравнение \(\sqrt{2x-1}\cdot ln(4x-a)=\sqrt{2x-1}\cdot ln(5x+a)\) имеет ровно 1 корень на отрезке \([0;1]\)?
Решение:
Перенесем все слагаемые в левую часть уравнения:
\(\sqrt{2x-1}\cdot (ln(4x-a)- ln(5x+a))=0.\)
Запишем в одну систему и ОДЗ, и равенство нулю первого или второго множителя.
\(\left\{\begin{matrix}
2x-1\geq 0, \\
4x-a > 0, \\
5x+a > 0, \\
\left[\begin{matrix}
x=\displaystyle \frac{1}{2}, \\
4x-a=5x+a;\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\)\(\left\{\begin{matrix}
x\geq \displaystyle \frac{1}{2}, \\
a < 4x, \\
a > -5x, \\
\left[\begin{matrix}
x=\displaystyle \frac{1}{2}, \\
x=-2a;\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \)\(\left[\begin{matrix}
\left\{\begin{matrix}
x=\displaystyle \frac{1}{2}, \\
\displaystyle -\frac{5}{2} < a < 2,\end{matrix}\right. \\
\left\{\begin{matrix}
x=-2a, \\
-2a\geq \displaystyle \frac{1}{2}, \\
a < -8a ,\\
a > 10a;\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \)\(\left[\begin{matrix}
\left\{\begin{matrix}
x=\displaystyle \frac{1}{2}, \\
-2,5 < a < 2,\end{matrix}\right. \\
\left\{\begin{matrix}
x=-2a, \\
a\leq -\displaystyle \frac{1}{4}.\end{matrix}\right.\end{matrix}\right.\)
Да, мы решили это уравнение. Нашли все его решения в зависимости от параметра \(a\).
Мы узнали, что при \(-2,5 < a < 2\) уравнение имеет корень \(x=\displaystyle \frac{1}{2}\). А при \(a\leq -\displaystyle \frac{1}{4}\) уравнение имеет корень \(x=-2a\).
Добавим условие \(x\in [0;1]\).
\(\left[\begin{matrix}
\left\{\begin{matrix}
x=\displaystyle \frac{1}{2}, \\
-2,5 < a < 2,\end{matrix}\right. \\
\left\{\begin{matrix}
x=-2a, \\
a\leq -\displaystyle \frac{1}{4}, \\
0\leq x\leq 1.\end{matrix}\right.\end{matrix}\right.\)
Первая система осталась без изменений, так как \(x=\displaystyle \frac{1}{2}\) лежит на отрезке \([0;1]\). Условие \(0\leq x\leq 1\) добавлено во вторую систему. А поскольку \(x=-2a\), получим:
\(\left[\begin{matrix}
\left\{\begin{matrix}
x=\displaystyle \frac{1}{2}, \\
-2,5 < a < 2,\end{matrix}\right. \\
\left\{\begin{matrix}
x=-2a, \\
a\leq -\displaystyle \frac{1}{4} ,\\
0\leq -2a\leq 1;\end{matrix}\right.\end{matrix}\right.\Leftrightarrow \left[\begin{matrix}
\left\{\begin{matrix}
x=\displaystyle \frac{1}{2}, \\
-2,5 < a < 2,\end{matrix}\right. \\
\left\{\begin{matrix}
x=-2a, \\
-\displaystyle \frac{1}{2}\leq a\leq -\frac{1}{4}.\end{matrix}\right.\end{matrix}\right.\)
Покажем на оси \(a\), при каких значениях параметра уравнение имеет решение \(x=\displaystyle \frac{1}{2}\) и при каких – решение \(x=-2a.\)
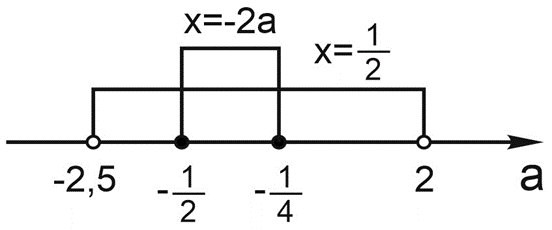
Для значений параметра \(a\in \left [ -\displaystyle \frac{1}{2};-\frac{1}{4} \right ]\) уравнение имеет два корня на отрезке \([0;1]\).
Если \(a\leq -2,5\) или \(a\geq 2\) – не имеет корней на данном отрезке.
А если \(a\in \left ( -2,5;-\displaystyle \frac{1}{2} \right )\cup \left ( -\displaystyle \frac{1}{4};2 \right )\) – уравнение имеет ровно один корень на данном отрезке. Но это ещё не ответ. Необходимо также проверить случай совпадения корней. Найти, при каком значении параметра корни \(x=\displaystyle \frac{1}{2}\) и \(x=-2a\) совпадают.
\(-2a=\displaystyle \frac{1}{2}; \; a=-\frac{1}{4}\). Объединим случаи.
Уравнение имеет на отрезке \([0;1]\) ровно один корень, если \(a\in \left ( -2,5;-\displaystyle\frac{1}{2} \right )\cup \left [ -\displaystyle\frac{1}{4};2 \right ).\)
Ответ: \(a\in \left ( -2,5;\displaystyle-\frac{1}{2} \right )\cup \left [ \displaystyle-\frac{1}{4};2 \right ).\)
4. При каких значениях параметра \(a\) уравнение \(x^2+(x-1)\cdot \sqrt{2x-a}=x\) имеет ровно 1 корень на отрезке \(x\in [0;1]\)?
Решение:
Запишем уравнение в виде \(x\cdot (x-1)+(x-1)\cdot \sqrt{2x-a}=0.\)
Разложим левую часть на множители:
\((x-1)\cdot (x+\sqrt{2x-a})=0.\)
Уравнение равносильно системе:
\(\left\{\begin{matrix}
\left[\begin{matrix}
x=1, \\
x=-\sqrt{2x-a},\end{matrix}\right. \\
2x-a\geq 0.\end{matrix}\right.\)
Добавим условие \(x\in [0;1]:\)
\(\left[\begin{matrix}
\left\{\begin{matrix}
x=1, \\
a\leq 2,\end{matrix}\right. \\
\left\{\begin{matrix}
x=-\sqrt{2x-a}, \\
2x-a\geq 0, \\
0\leq x\leq 1.\end{matrix}\right.\end{matrix}\right.\)
Упростим вторую систему. Посмотрим на первое ее уравнение.
Так как \(x\geq 0\), то \(-\sqrt{2x-a}\geq 0\). Это значит, что \(\sqrt{2x-a}\leq 0\).
А поскольку арифметический квадратный корень не может быть отрицательным, остаётся только случай \(\sqrt{2x-a}=0\).
Тогда из первого уравнения этой системы \(x=0\), а также \(a=0\).
Вот что получается:
\(\left[\begin{matrix}
\left\{\begin{matrix}
x=1, \\
a\leq 2,\end{matrix}\right. \\
\left\{\begin{matrix}
x=0, \\
a=0.\end{matrix}\right.\end{matrix}\right.\)
При всех \(a\leq 2\) исходное уравнение имеет корень \(x=1\), принадлежащий отрезку \([0;1]\). А при \(a=0\) добавляется ещё и второй корень \(x=0\), который нам не нужен. Значит, уравнение имеет единственный корень на отрезке \([0;1],\) если \(a\leq 2\) и \(a\neq 0\).
Ответ: \(a\in (-\infty ;0)\cup (0;2]\).