Четные и нечетные функции

Функция $y=f(x)$ называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

$f(-x)=f(x).$

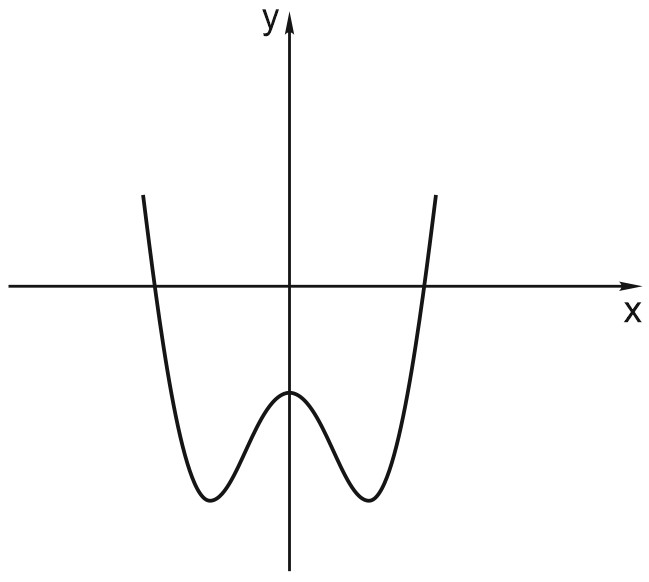
График четной функции симметричен относительно оси ординат.

Например, $y = x^2, y = cos x, y = \left |x \right |$ — четные функции.

Функция $y=f(x)$ называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

$f(-x)=-f(x).$

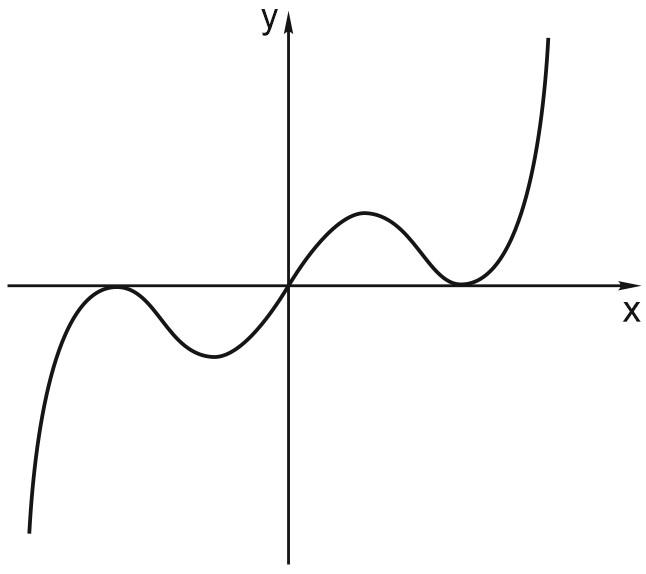
График нечетной функции симметричен относительно начала координат.

Например, $y = x^3, y = sin x, y = tg x, y=\frac{1}{x}$ — нечетные функции.

Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.

Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:

1. Проверьте, является ли функция $f(x)=\frac{x}{3}-\frac{3}{x}$ четной (нечетной).

Область определения функции $f(x):$

$x\ne 0.$

Проверим, является ли $f(x)$ чётной или нечётной. Если $f(-x)=f(x),$ функция четна. Если $f(-x)=-f(x),$ функция нечетна.

$f(-x)=-\frac{x}{3}+\frac{3}{x}=-(\frac{x}{3}-\frac{3}{x})=-f(x)$ — значит, функция $f(x)=\frac{x}{3}-\frac{3}{x}$ нечётная, её график симметричен относительно нуля.

2. Проверьте, является ли функция $f(x)=x^2+cosx$ четной (нечетной).

Область определения: все действительные числа.

$f(x)$ — чётная, как сумма двух чётных функций.

$f(-x)={(-x)}^2+cos(-x)=x^2+cosx=f(x).$

Её график симметричен относительно оси y.

3. Проверьте, является ли функция $f(x)=\frac{\sqrt{1-x^2}}{\left|x\right|}$ четной (нечетной).

$D(f):x\in [-1;0)\cup (0;1] .$

Область определения функции симметрична относительно нуля.

$f(-x)=\frac{\sqrt{1-{(-x)}^2}}{\left|-x\right|}=\frac{\sqrt{1-x^2}}{\left|x\right|};$

$f(x)$ — чётная, её график симметричен относительно оси y.

Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Четные и нечетные функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 08.03.2023

Это полезно