Часть 1. Задания с кратким ответом
1. В 11 «А» классе 27 учеников, причем девочек на 25% больше, чем мальчиков. Сколько девочек в 11 «А»?
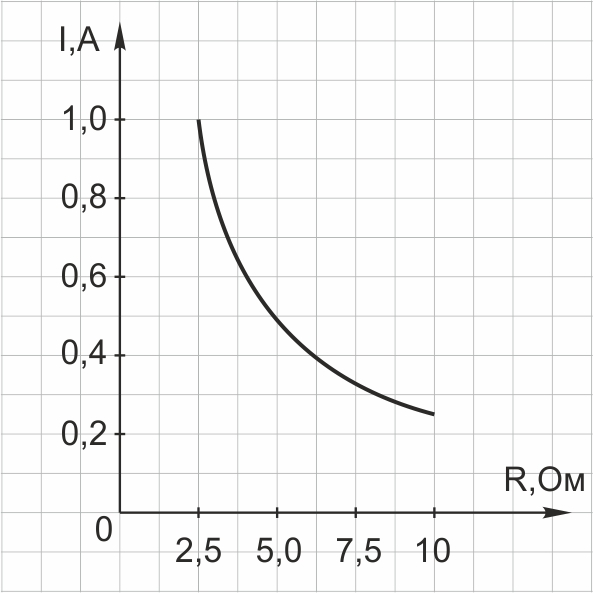
2. На рисунке представлен график зависимости силы тока (в амперах) в проводнике от его сопротивления (в омах). По графику определите силу тока при сопротивлении 5 Ом. Ответ выразите в амперах.
3. Найдите площадь фигуры, изображенной на клетчатой бумаге с размером клетки \(1\) см \(\times 1\) см. Ответ дайте в квадратных сантиметрах.
4. Известно, что в семье Ивановых четверо детей. Найдите вероятность того, что ровно трое из четырех детей – девочки.
5. Решите уравнение: \({log_2}^2x+log_2x=0.\)
Если уравнение имеет несколько корней, в ответе запишите меньший корень.
6. Прямая, параллельная основаниям \(AD\) и \(BC\) трапеции \(ABCD\) и проходящая через точку пересечения ее диагоналей, пересекает боковые стороны трапеции в точках \(M\) и \(N\). Найдите \(MN\), если \(AD = 7, \; BC = 3.\)
7. На рисунке изображен график \(y=f'(x)\) - производной непрерывной функции \(y=f(x)\). В какой точке функция \(y=f(x)\) принимает наименьшее значение?
8. Найдите объем детали, изображенной на рисунке, если диаметр основания цилиндра равен 10, высота равна \(\frac{4}{\pi}\), а диаметр цилиндрического отверстия равен 4.
9. Найдите значение выражения: \(\displaystyle \frac{1}{2}+sin\frac{\pi}{12}sin\frac{5\pi}{12}-sin^2\frac{\pi}{3}.\)
10. При параллельном соединении резисторов с сопротивлениями \(R_1\) и \(R_2\) общее сопротивление \(R\) рассчитывается по формуле \(\displaystyle \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}.\) Сопротивление \(R_1\) можно изменять в пределах от 120 до 200 Ом, а сопротивление \(R_2\) в пределах от 600 до 720 Ом. Найдите наименьшее возможное значение сопротивления \(R_1\), при котором общее сопротивление участка цепи равно 120 Ом. Ответ выразите в Омах.
11. Анна Малкова. Из пункта \(A\) выехал автомобиль «Ока». В тот же момент из пункта \(B\) навстречу ему выехал автомобиль «Пежо» со скоростью на 35 км/ч большей, чем у «Оки», и через 5 часов проехал мимо «Оки». Через час после выезда «Оки» из пункта \(A\) стартовал автомобиль «Лада Калина» со скоростью на 4 км/ч большей, чем у «Оки», и достиг пункта \(B\) одновременно с «Окой». Найдите скорость автомобиля «Ока». Ответ выразите в км/ч.
12. Найдите наименьшее значение функции \(y=3cosx-\pi x+\pi^2\) на отрезке \([-2\pi; \pi].\)
Часть 2. Задания с развернутым ответом
13. а) Решите уравнение: \(\displaystyle \frac{1}{sinx}+\frac{1}{cosx}=2\sqrt2.\)
б) Найдите все корни уравнения на отрезке \(\left[-\displaystyle \frac{\pi}{3}; \pi\right].\)
14. Анна Малкова. В треугольной пирамиде \(SABC\) все плоские углы при вершине \(S\) – прямые, длины ребер \(SA, \; SB\) и \(SC\) равны \(\sqrt{\sqrt5+\sqrt3}, \sqrt{\sqrt5-\sqrt3}\) и \(6\sqrt2\) соответственно. Плоскость \(\alpha \) проходит через середины ребер \(SA, \; SC\) и \(BC\).
а) Докажите, что сечение пирамиды плоскостью \(\alpha \) является прямоугольником.
б) Найдите объем пирамиды с вершиной \(S\), основанием которой является сечение пирамиды \(SABC\) плоскостью \(\alpha \).
15. Решите неравенство: \(\sqrt{log_3x}+2\sqrt{log_x3}\geq3.\)
16. Антон Акимов В трапеции \(ABCD\) точки \(M\) и \(N\) — середины боковых сторон \(AB\) и \(CD\) соответственно. Известно, что \(AD = 14, \; CM = 5, \; AN = 5\), а высота трапеции равна \(8\).
а) Докажите, что около трапеции \(ABCD\) нельзя описать окружность.
б) Известно, что \(AD > BC\). Найдите площадь трапеции \(ABCD\).
17. Анна Малкова 15-го января 2018 года Роман взял в банке кредит на сумму 5 020 000 рублей на срок 24 месяца.
Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму Роман вернёт банку в течение трех летних месяцев 2018 года?
18. Анна Малкова
При каких значениях параметра \(a\) уравнение \(\sqrt{x^2-4ax+4a^2}-\sqrt{x^2+6ax+9a^2}=4sinx.\)
имеет бесконечно много решений?
19. В коробке находятся 13 красных и 17 белых фишек; есть также неограниченное число фишек того и другого цвета. Разрешается совершать в любом порядке и в любом количестве следующие действия:
- Увеличить на 2 число красных фишек и одновременно уменьшить на 1 число белых,
- Увеличить на 1 число красных фишек и одновременно увеличить на 2 число белых,
- Уменьшить на 2 число красных фишек и одновременно увеличить на 1 число белых,
- Уменьшить на 1 число красных фишек и одновременно уменьшить на 2 число белых,
а) Может ли в коробке в результате 8 действий остаться ровно 30 фишек?
б) Может ли в результате некоторого числа действий получиться 37 красных и 43 белых фишек?
в) Какое наименьшее число фишек может получиться?
- ЕГЭ-Студия приглашает составителей задач в формате ЕГЭ. Работа оплачивается.
- ВНИМАНИЕ преподавателям и владельцам образовательных сайтов. Мы настоятельно просим вас НЕ ВЫКЛАДЫВАТЬ в интернет условия и тем более решения задач. Мы хотим, чтобы участники имели возможность честно решить задачи.
Скачать вариант в pdf.