Это знакомый нам графический способ решения, к которому добавляется немного геометрии и тригонометрии. Например, решение прямоугольных треугольников, формулы тригонометрии, свойства касательных к окружности.
Также здесь используется формула расстояния от точки до прямой из аналитической геометрии.
1. Анна Малкова. При каких значениях параметра \(a\) система имеет ровно 2 решения?
\(\left\{\begin{matrix}
(x^2+y^2-6y)(\sqrt{36-x^2}-y)=0, \\
x=a(y+2).\end{matrix}\right.\)
Решение:
Как обычно, упрощаем исходную систему, используя цепочку равносильных переходов.
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю, а другой при этом имеет смысл. Значит, первое уравнение равносильно совокупности двух уравнений при условии \(36-x^2\geq 0\).
\(\left\{\begin{matrix}
(x^2+y^2-6y)(\sqrt{36-x^2}-y)=0, \\
x=a(y+2);\end{matrix}\right.\Leftrightarrow \)\(\left\{\begin{matrix}
\left[\begin{matrix}
x^2+y^2-6y=0, \\
y=\sqrt{36-x^2},\end{matrix}\right. \\
36-x^2\geq 0,\\
x=a(y+2);\end{matrix}\right.\Leftrightarrow \)\(\left\{\begin{matrix}
\left[\begin{matrix}
x^2+(y^2-6y+9)=9, \\
y=\sqrt{36-x^2},\end{matrix}\right. \\
|x|\leq 6,\\
x=a(y+2).\end{matrix}\right.\)
Мы выделили в первом уравнении полный квадрат, чтобы привести его к уравнению окружности.
\(\left\{\begin{matrix}
\left[\begin{matrix}
x^2+(y-3)^2=9,\\
y=\sqrt{36-x^2},\end{matrix}\right. \\
-6\leq x\leq 6,\\
x=a(y+2).\end{matrix}\right.\)
Решим систему графически.
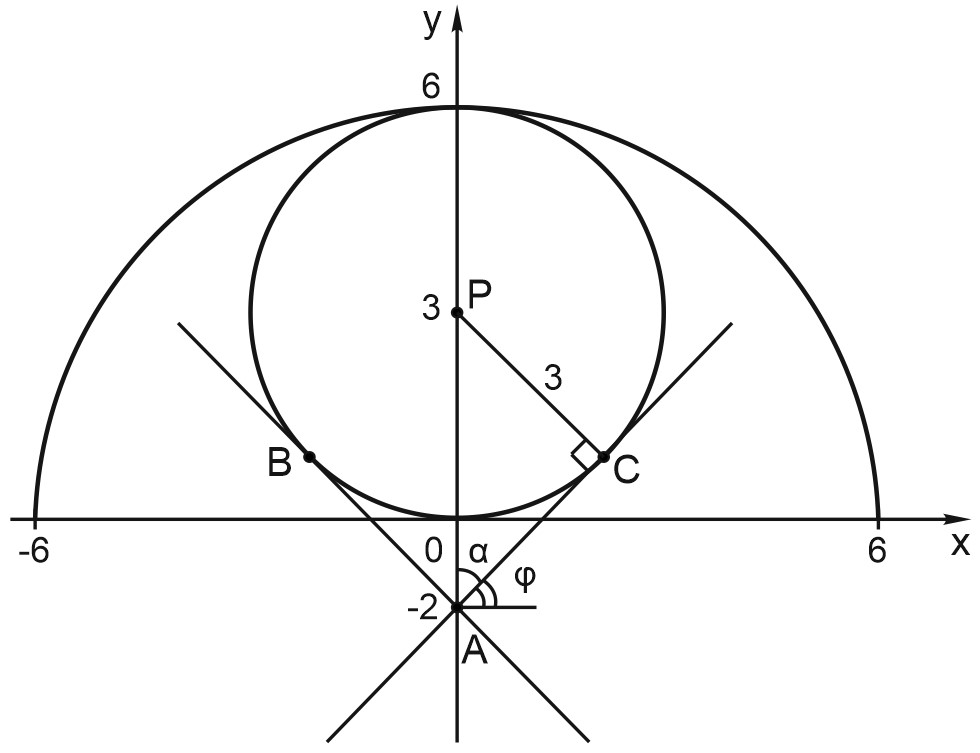
Уравнение \(x^2+(y-3)^2=9\) задаёт окружность с центром \(P(0;3)\) и радиусом \(3\).
Уравнение \(y=\sqrt{36-x^2}\) задаёт верхнюю полуокружность с центром в начале координат и радиусом \(6\).
График первого уравнения исходной системы – это совокупность окружности с центром \(P(0; 3)\) с радиусом \(3\) и верхней полуокружности с центром \(O(0; 0)\) и радиусом \(6\).
Рассмотрим уравнение \(x=a(y+2)\). Уравнение линейное, и его графиком должна быть прямая. Однако в нем есть нечто необычное: \(x\) выражен через \(y\), а не наоборот.
Если \(a=0\), то это прямая \(x=0\) (ось ординат).
Если \(a\neq 0\), то есть возможность поделить на \(a\) обе части уравнения.
Получаем при \(a\neq 0\), что \(y=\displaystyle \frac{x}{a}-2\).
Уравнение задаёт семейство прямых, проходящих через точку \(A(0;-2)\) с угловым коэффициентом, равным \(\displaystyle \frac{1}{a}\).
Случай \(a=0\) нам подходит, потому что прямая \(x=0\) пересекает график первого уравнения ровно в двух точках.
Нам подходят также случаи касания прямой \(x=a(y+2)\) c графиком первого уравнения в точках \(B\) и \(C\). Значения параметра в этих случаях найдем геометрическим способом.
Как мы помним из геометрии, касательная перпендикулярна радиусу, проведенному в точку касания.
Рассмотрим треугольник \(ACP\).
\(\angle ACP=90^\circ , \; PC=3, \; AP=2+3=5\) следовательно, \(AC=4\).
\(tg\alpha =\displaystyle \frac{PC}{AC}=\displaystyle \frac{3}{4}\).
Тогда \(tg\varphi =tg(90^\circ -\alpha )=ctg\alpha =\displaystyle \frac{4}{3};\)
\(tg\varphi =\displaystyle \frac{1}{a}\), значит, в точке \(C\) значение параметра \(a\) равно \(\displaystyle \frac{3}{4}.\)
Для точки \(B\): \(a=-\displaystyle \frac{3}{4}.\)
Ответ: \(-\displaystyle \frac{3}{4}; \; 0; \; \frac{3}{4}\).
2. Найдите все значения параметра \(a\), при каждом из которых система уравнений
\(\left\{\begin{matrix}
2x^2+2y^2=5xy, \\
(x-a)^2+(y-a)^2=5a^4\end{matrix}\right. \; \) имеет ровно два решения.
Решение:
Упростим первое уравнение системы.
\(2x^2+2y^2=5xy\Leftrightarrow 2x^2-5xy+2y^2=0\).
Это однородное уравнение, все слагаемые в левой части – второй степени.
Одно из решений этого уравнения – пара чисел \((0;0)\).
Пусть \(y\neq 0\), получим: \(2\left (\displaystyle \frac{x}{y}\right)^2-5\displaystyle \frac{x}{y}+2=0\).
Сделаем замену переменной: \(\displaystyle \frac{x}{y}=t\).
\(2t^2-5t+2=0;\)
\(D=25-16=9.\)
\(t=\displaystyle \frac{5\pm 3}{4}; \; t=2\) или \(t=\displaystyle \frac{1}{2}\), значит, \(x=2y\) или \(x=\displaystyle \frac{y}{2}\).
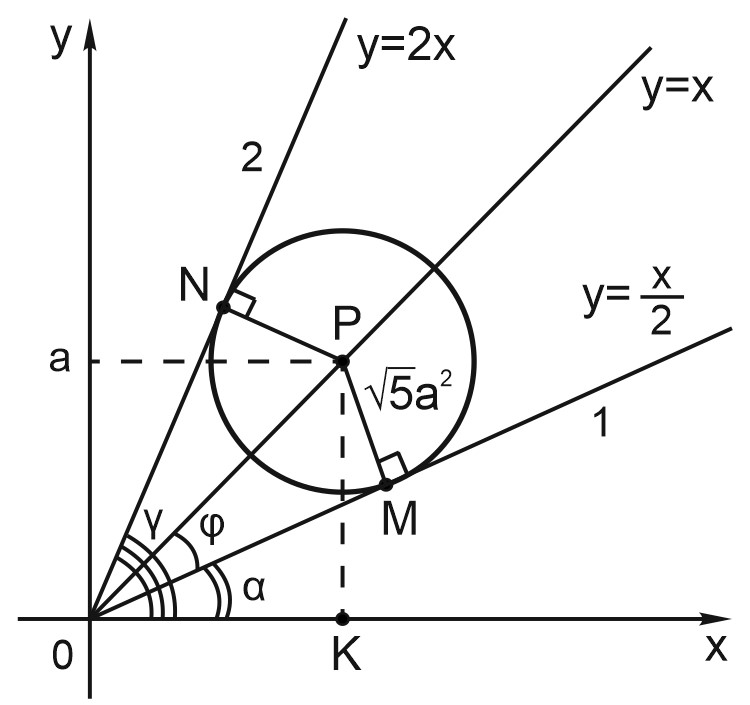
Первое уравнение задаёт пару прямых \(y=\displaystyle \frac{x}{2}\) и \(y=2x\). Второе уравнение системы задаёт окружность с центром \((a; a)\), с радиусом \(R=\sqrt{5} a^2\).
Центр окружности лежит на прямой \(y=x\).
Исходная система имеет ровно \(2\) решения, если окружность имеет ровно \(2\) общие точки с данными прямыми.
Поскольку центр окружности лежит на прямой \(y=x\), окружность симметрична относительно этой прямой.
Функции \(y=2x\) и \(y=\displaystyle \frac{x}{2}\) взаимно обратны, поэтому их графики - прямые \(y=2x\) и \(y=\displaystyle \frac{x}{2}\), - также симметричны относительно прямой \(y=x\).
И если окружность с центром на прямой \(y=x\) касается одной из этих прямых, то она касается и второй. Только в таком случае исходная система имеет ровно \(2\) различных решения.
Пусть \(P(a;a)\) – центр окружности, заданной вторым уравнением.
Решим задачу с помощью формулы расстояния от точки до прямой.
Расстояние \(d\) от точки \(P(x_0; y_0)\) до прямой \(Ax+By+C=0\) выражается формулой:
\(d=\displaystyle \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}.\)
В нашем случае прямую \(y=\displaystyle \frac{x}{2}\) можно записать в виде \(x-2y=0\). Мы помним из геометрии, что если прямая касается окружности, то расстояние от центра окружности до этой прямой равно радиусу окружности.
Тогда \(d=R=\displaystyle \frac{|a-2a|}{\sqrt{1+4}}=\displaystyle \frac{|a|}{\sqrt{5}};\)
\(a^2\sqrt{5}=\displaystyle \frac{|a|}{\sqrt{5}},\) отсюда \(\left[\begin{matrix}
\left| a\right|=\displaystyle \frac{1}{5},\\\left| a\right|=0;
\end{matrix}\right. \; \) то есть \(\left[\begin{matrix}
a=\pm \displaystyle \frac{1}{5},\\ a=0.
\end{matrix}\right. \)
А как же случай \(y=0\), о котором мы говорили в начале? Действительно, пара чисел \((0; 0)\) – решение первого уравнения.
При подстановке во второе уравнение она дает значение \(a=0\). При таком значении параметра система имеет единственное решение \((0; 0)\), а это нам не подходит.
Ответ: \(a=\pm \displaystyle \frac{1}{5}\).