Начиная решение задачи с параметром, мы задаем себе вопрос: можно ли это нарисовать? Если нельзя – стараемся упростить исходное уравнение или систему с помощью цепочки равносильных переходов и все-таки нарисовать.
При этом рисунок – еще не решение. Надо написать, что именно на нем изображено. Куда смотреть, как рисунок связан с условием задачи.
Фразу «Из рисунка видно…» писать не надо. Надо рассказать, что же изображено на рисунке.
Мы покажем вам план – что и как надо написать, чтобы получить за «параметр» полный балл на ЕГЭ. Этот план очень простой.
Помните, в средней школе мы писали сочинение по картинам художников. Например, по картине Ф. Решетникова «Опять двойка».
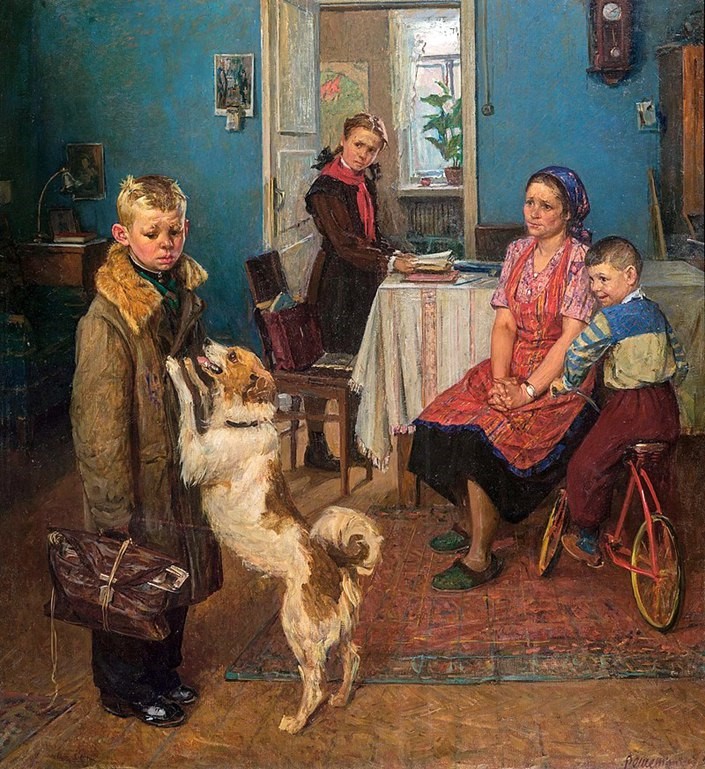
Мы писали примерно так:
«Перед нами главный герой. Он только что принес из школы «двойку». Мальчик так расстроен, что прямо в пальто и ботинках прошел в комнату и не знает, как быть дальше. Его портфель перевязан веревкой, потому что коньки в него не помещаются.
Наш герой не привык к двойкам. Название картины подсказывает, что это не первая двойка, но и не 125-я по счету. Может быть, вторая или третья. Школьник с портфелем застыл посреди комнаты, а все смотрят на него.
Добрая мама – с напряженным сочувствием. Но кажется, она вот-вот скажет: «Да сколько же можно?» Сестра-отличница глядит осуждающе. Она только пришла из школы, и сразу за уроки. У нее двоек быть не может, одни пятерки! Младший братец – с ехидным любопытством. Оказывается, и у старшего бывают неприятности! И только собака, верный друг, хвост бубликом, рада мальчику и принимает его таким, какой он есть!»
Так же, как картину «Опять двойка», мы описываем решение задачи с параметрами.
Кто изображен на картине,
Что они делают,
Как мы узнали о том, что здесь происходит,
- и отвечаем на вопрос задачи.
1) Первый шаг оформления – рассказать, какие линии изображены на рисунке.
Например:
«Графиком функции \(f(x)\) является парабола с ветвями вверх и вершиной в точке \(M (1; 1)\), а графиком функции \(g(x)\) является прямая \(y=x+a\), сдвинутая по вертикали вверх или вниз в зависимости от значения параметра \(a\)».
Так же, как и в геометрии, мы обозначаем точки большими латинскими буквами.
2) Второй шаг: мы показываем проверяющему, куда именно ему смотреть. Другими словами – как связан наш чертеж с условием задачи. Например: «Исходное уравнение имеет единственное решение, если прямая \(y=x+a\) пересекает график функции \(f(x)\) ровно один раз в заданной области. Это происходит, только если она проходит выше точки \(A\) и ниже точки \(B\) или через точку \(B\)».
3) Следующий этап – поиск координат точек \(A\) и \(B\) и соответствующих значений параметра \(a\). И наконец – запись ответа.
Пример решения и оформления задачи с параметром
Найдите все значения параметра \(a\), при каждом из которых система
\(\left\{\begin{matrix}
y^2+xy-4x-9y+20=0, \\
y=ax+1, \\
x>0\end{matrix}\right.\) имеет единственное решение.
Решение:
Преобразуем первое уравнение, разложив его левую часть на множители:
\((y-4)x+y^2-9y+20=(y-4)x+(y-4)(y-5)=(y-4)(x+y-5)\).
Так как \((y-4)(x+y-5)=0\), исходная система примет вид:
\(\left\{\begin{matrix}
\left[\begin{matrix}
y=4, \\
y=5-x,\end{matrix}\right. \\
y=ax+1,\\
x > 2.\end{matrix}\right.\)
Графиком первого уравнения является совокупность прямых \(y=4\) и \(y=5-x\).
График второго уравнения – пучок прямых \(y=ax+1\) с угловым коэффициентом \(a\), проходящих через точку \(C (0; 1).\)
Система имеет единственное решение, если в области, заданной неравенством \(x > 2\), прямая \(y=ax+1\) пересекает график первого уравнения ровно один раз.
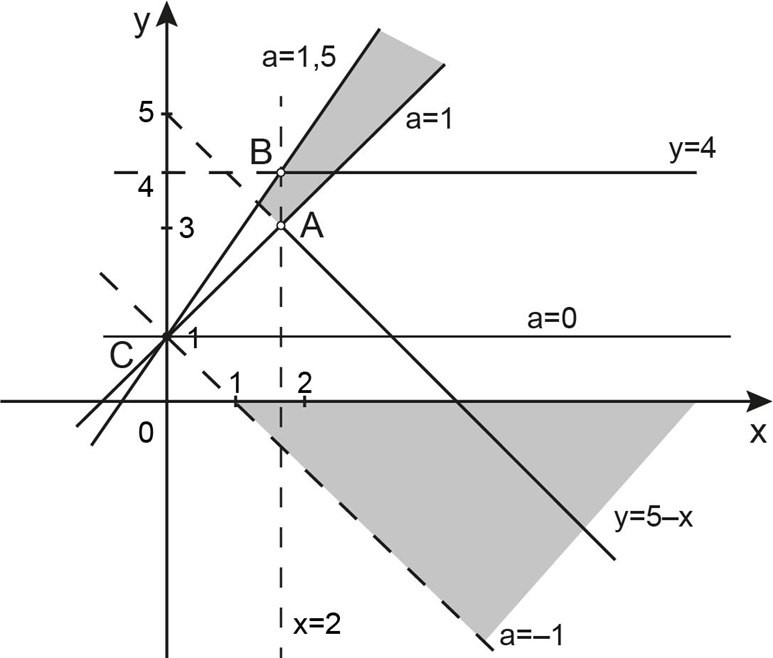
Это происходит в следующих случаях:
1) Прямая \(y=ax+1\) проходит выше точки \(A\) или через точку \(A\) и ниже точки \(B\). В точке \(A\) пересекаются прямые \(y=5-x\) и \(x=2\), в точке \(B\) пересекаются прямые \(y=4\) и \(x=2\).
2) Если \(a=0\), система имеет единственное решение. В этом случае прямая \(y=ax+1\) не пересекает прямую \(y=4\), то есть параллельна ей.
3) Если \(-1 < a < 0\), система имеет единственное решение.
В остальных случаях система не имеет решений или имеет больше одного решения.
Найдем координаты точек \(A\) и \(B\) и значения параметра для этих точек.
1) Точка \(A\). Подставив \(x=2\) и \(y=5-2=3\) в уравнение прямой \(y=ax+1\) находим, что для точки \(A\) значение параметра \(a=1\).
2) Точка \(B\). Подставив \(x=2\) и \(y=4\) в уравнение \(y=ax+1\) получим, что \(a=1,5\).
Точка \(B\) – пустая. Если прямая \(y=ax+1\) проходит через точку \(B\), система не имеет решений.
Если прямая \(y=ax+1\) проходит ниже точки \(A\), в которой пересекаются прямые \(y=5-x\) и \(x=2\), добавляется второе решение. Такие случаи нам не подходят.
Если \(a=-1\), прямая \(y=ax+1\) становится параллельной прямой \(y=5-x\) и система не имеет решений.
При \(a < -1\) или \(a > 1,5\) исходная система также не имеет решений.
Мы рассмотрели все возможные значения \(a\). Объединив подходящие случаи, получим ответ.
Ответ: \(a\in (-1;0]\cup [1;1,5)\)
































