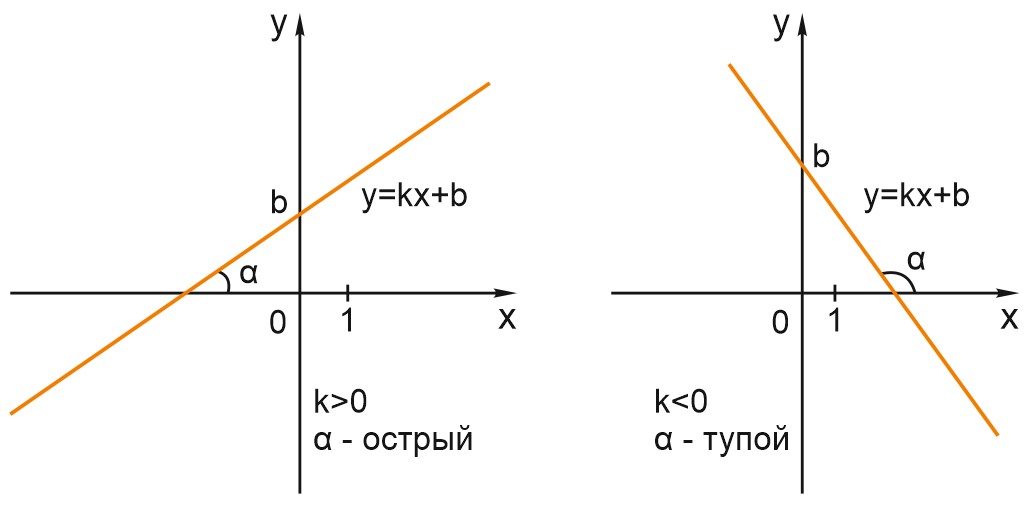Линейная функция — функция вида \(y = kx+b.\) График линейной функции — прямая.
Для построения графика линейной функции достаточно двух точек — потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.
Угловой коэффициент прямой
Величина \(k\) в формуле линейной функции \(y = kx+b \) называется угловым коэффициентом прямой
Если \(k> 0\), линейная функция возрастает. Чем больше \(x\), тем больше \(y\), то есть график идет вправо и вверх.
Если \(k< 0\), линейная функция убывает. Чем больше \(x\), тем меньше \(y\), то есть график идет вправо и вниз.
Угловой коэффициент \(k\) равен тангенсу угла наклона графика линейной функции к положительному направлению оси \(X\).
\( k= tg \alpha.\)
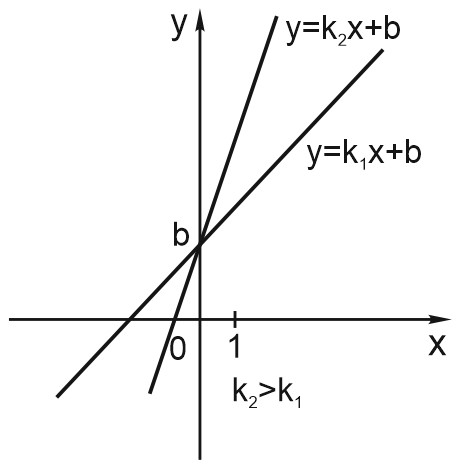
Пусть \(k> 0.\) Чем больше \(k\), тем круче вверх идет график функции.
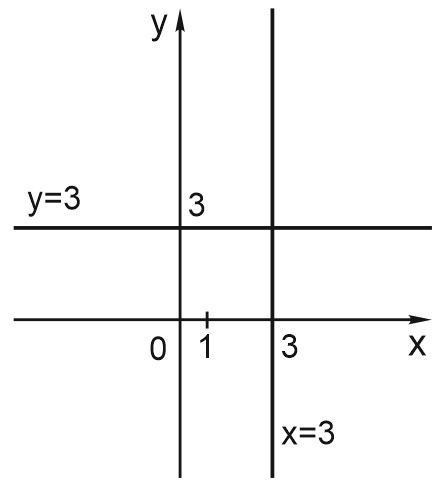
А что же будет, если \(k=0\)? Мы получим горизонтальную прямую \(y = b.\) На рисунке показан график функции \(y = 3.\)
Заметим, что прямая \(x = 3\) (также изображенная на рисунке) не является графиком функции в нашем обычном, школьном смысле слова. В самом деле — мы помним, что функция — это соответствие между двумя множествами, причем каждому элементу множества \(X\) соответствует один и только один элемент множества \(Y\).
Для прямой \(x = 3\) это не выполняется: значению \(x = 3\) соответствует бесконечно много значений \(y\).
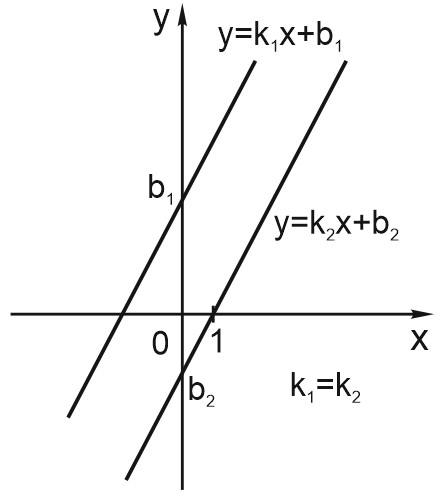
Если \(k_1{=k}_2,\) прямые параллельны.
При этом, чем больше \(b\), тем выше расположен на координатной плоскости график функции.
Например, прямые \(y = 4 x + 3\) и \(y = 4 x + 9\) параллельны. Их угловые коэффициенты равны.
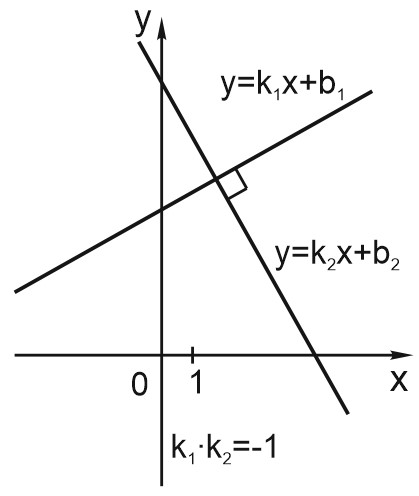
Если \( k_1\, k_2=-1,\) прямые перпендикулярны. Например, прямые \(y = 4x + 3\) и \(y = - 0,25 x - 1\) пересекаются под прямым углом. Произведение их угловых коэффициентов равно \(-1\).
Построение графика линейной функции
График линейной функции построить легко — достаточно двух точек.
Оказывается, что привычный нам вид уравнения прямой \(y = kx+b\) — не единственно возможный.
Уравнение прямой можно записать также в виде \( Ax + By + C = 0. \)
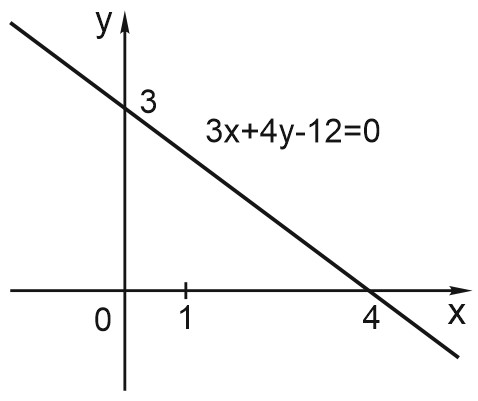
Построим, например, прямую, заданную уравнением \(3x + 4y - 12 = 0.\)
При \(x = 0\) получаем, что \(y = 3. \)
При \(y = 0\) получаем, что \( x = 4. \)
Значит, наша прямая проходит через точки \( M (0; 3)\) и \(N (4; 0).\)
Выразив \(y\) из уравнения \(Ax + By + C = 0\), получим уравнение прямой вида \(y = kx+b.\)
Если вы поступаете в вуз на специальность, связанную с математикой, - уже на первом курсе вы познакомитесь и с другими видами уравнения прямой.
Зачем изучать линейную функцию?
Дело в том, что многие зависимости в природе и технике описываются формулой вида \( y = kx+b.\)
Например, закон Ома для участка цепи: \(U = I R.\) Напряжение \(U\) прямо пропорционально силе тока \(I\).
Формула для равномерного прямолинейного движения: \(S= vt\). Пройденное расстояние \(S\) прямо пропорционально времени \(t\).
Закон теплового расширения \(l\left(t\right)=l_0\left(1+ \alpha \cdot t\right)\), который вам встретится в одной из задач под номером 9 варианта Профильного ЕГЭ по математике — тоже линейная функция. И таких примеров можно привести очень много.
Обратите внимание, что в формулу линейной функции \( y = kx+b\) аргумент х входит в первой степени. Мы просто умножаем х на угловой коэффициент \(k\) и прибавляем \(b\).
Если в формулу функции входит аргумент в любой другой степени — например, в квадрате или в кубе, если мы делим на \(x\), если в формуле присутствует \(sin x, \; \displaystyle\frac{1}{x}\) или \(\sqrt{x}\), или показательные или логарифмические выражения, зависящие от \(x\), - график функции уже не будет прямой линией.