Основная теорема арифметики: Любое натуральное число можно представить в виде произведения простых делителей, взятых в натуральных степенях, причем это разложение единственно.
\(a=p_{1}^{n_{1}}p_{2}^{n_{2}}... p_{s}^{n_{s}}.\)
Например, \(72=2^{3}\cdot 3^{2}.\)
Количество делителей натуральных чисел равно \((n_{1}+1)(n_{2}+1)...(n_{s}+1).\)
Например, количество делителей числа \(72\) равно \((3+1)(2+1)=12.\)
Напомним, что простые числа — те, что делятся только на себя и на единицу. Единица не является ни простым, ни составным числом. Простые числа: \(2, \; 3, \; 5, \; 7, \; 11, \; 13, \; 17, \; 19... \)
Начинаем с моей авторской задачи. В ней используется четность чисел и основная теорема арифметики.
1. Известно, что \(A\) — двузначное число.
а) Может ли число \(A^{2}\) оканчиваться на \(A-1\)?
б) Может ли число \(A^{2}\) оканчиваться на \(A-2\)?
в) Известно, что число \(A^{2}\) оканчивается на \(A\). Найдите все возможные значения \(A\) (не пользуясь калькулятором и таблицей квадратных натуральных чисел).
Решение:
а) Нет, не может. Если \(A\) — четное, то \(A-1\) — нечетное и последняя цифра числа \(A-1\) — нечетная. При этом \(A^{2}\) — четное, противоречие.
Аналогично, если \(A\) — нечетное, то \(A^{2}\) — нечетное, \(A-1\) — четное, противоречие.
б) Нет, не может. Напишем, на какую цифру может оканчиваться число \(A\) и число \(A^{2}\).
| \(A\) оканчивается на | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) | \(0\) |
| \(A^{2}\) оканчивается на | \(1\) | \(4\) | \(9\) | \(6\) | \(5\) | \(6\) | \(9\) | \(4\) | \(1\) | \(00\) |
Условие не выполняется ни для одного значения последней цифры числа \(A\).
в) Это числа \(25\) и \(76; \; 25^{2}=625, \; 76^{2}=5776\), и других чисел, удовлетворяющих условию, нет.
Докажем это.
Запишем число \(A\) в виде \(10a+b\).
Так как \(A^{2}\) оканчивается на \(A\), получим:
\((10a+b)^{2}=100\cdot c+(10a+b)\), то есть \(A^{2}=100\cdot c+A\).
\(A^{2}-A=100\cdot c\), где \(c\in N\), значит, \((A^{2}-A)\vdots 100; \; 100= 2^{2}\cdot 5^{2}.\)
Мы представили число \(100\) в виде произведения простых множителей, взятых в натуральных степенях.
Значит, \(A(A-1)\vdots (2^{2}\cdot 5^{2}).\)
Случай, когда \(A\vdots 5\) и \((A-1)\vdots 5\) невозможен, так как \((A-1)\) и \(A\) — последовательные натуральные числа.
Значит, \(A\vdots 25\) или \((A-1)\vdots 25\). Так как \(A\) — двузначное, возможны следующие случаи:
1) \(A=25, \; A-1=24\) — подходит, \((A-1)\vdots 4\);
2) \(A-1=25, \; A=26\) — не подходит, так как \(26\) не делится на \(4\);
3) \(A=50, \; A-1=49\) или \(A-1=50, \; A=51\) — не подходит, \(A(A-1)\) не делится на \(4\);
4) \(A=75, \; A-1=74\) — не подходит;
5) \(A=76, \; A-1=75\) — подходит.
Мы нашли, что \(A=25\) или \(A=76\), и других вариантов нет. Действительно, \(25^{2}=625, \; 76^{2}=5776.\)
Разберем типичную задачу ЕГЭ на основную теорему арифметики.
2. Длины сторон прямоугольника — натуральные числа, а его периметр равен \(200\). Известно, что длина одной стороны прямоугольника равна \(n\)% от длины другой стороны, где \(n\) — также натуральное число.
а) Какое наибольшее значение может принимать площадь прямоугольника?
б) Какое наименьшее значение может принимать площадь прямоугольника?
в) Найдите все возможные значения, которые может принимать площадь прямоугольника, если дополнительно известно, что \(n> 100\).
Решение:
Пусть \(a\) и \(b\) — стороны прямоугольника.
Периметр прямоугольника \(2(a+b)=200,\)
\(a+b =100,\)
\(b= 100-a.\)
Площадь прямоугольника \(S(a)=ab=a(100-a).\)
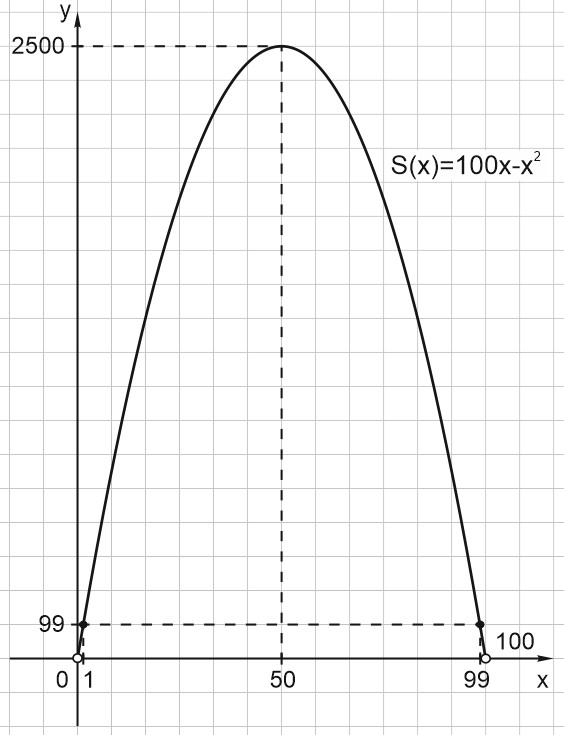
Нарисуем график функции \(S(x)=100x-x^{2}\), которая совпадает с \(S(a)\) при натуральных значениях \(x\). Это парабола с ветвями вниз.
а) Наибольшее значение функции \(S(x)=100x-x^{2}\) достигается в вершине параболы, при \(x=50\).
\(S_{max}(x)=S(50)=50^{2}=2500.\)
При этом \(a=50, b=50, \; S_{max}=2500\). Это наибольшее значение площади прямоугольника (он оказался квадратом).
б) График функции \(S(x)\) — парабола с ветвями вниз. Функция \(S(x)\) совпадает с \(S(a)\) при натуральных \(x\), причем \(x< 100\).
Поскольку график функции \(S(x)\) симметричен относительно прямой \(x=50\) и при \(x\in [0; 50] \; S(x)\) монотонно возрастает, \(a\) при \(x\in [50; 100] \; S(x)\) монотонно убывает. Натуральным \(a\), наиболее близким к концу отрезка \([0; 100]\), будут соответствовать наименьшему значению \(S(a)\).
При \(a=1\) или \(a=99\) выражение \(S(a)\) принимает наименьшее значение и равно \(1\cdot 99=99\).
По условию, длина одной стороны составляет \(n\)% от длины другой.
Если \(a=1, \; b=99,\) то \(b=\displaystyle \frac{99}{100}\cdot 100\cdot a=9900\)%\(a\), условие выполнено.
в) Пусть \(n> 100, \; b\) — большая сторона прямоугольника, \(b=\displaystyle \frac{an}{100}\).
Поскольку \(S=ab=a\cdot \displaystyle \frac{n}{100}\cdot a=\displaystyle \frac{a^{2}-n}{100},\)
периметр равен \(2(a+b)=2a\left(1+\displaystyle \frac{n}{100}\right);\)
\(2a\left (1+\displaystyle \frac{n}{100}\right)=200;\)
\(a\left (1+\displaystyle \frac{n}{100}\right)=100;\)
\(a(100+n)=10000.\)
Мы получим, что \(10000\vdots a.\)
Так как \(a\) — меньшая сторона прямоугольника, \(a< 50\). Найдем делитель числа \(10000\), меньше \(50\).
\(10000=10^{4}=2^{4}\cdot 5^{4}.\)
Мы представили число \(10000\) в виде произведения простых множителей, взятых в натуральных степенях. Применим основную теорему арифметики.
\(10000\vdots a\). Значит, что число \(a\) содержит только множители \(2^{k}\) и \(5^{k},\) где \(k\leq 4\).
Рассмотрим возможные случаи:
1) Число \(a\) содержит только степени двойки, \(a=1, \; 2, \; 4, \; 8\) или \(16\).
2) Если \(a\) делится на \(5\), но не делится на \(25\), возможно случаи \(a=5, \; 10, \; 20\) или \(40\).
3) Если \(a\vdots 25\), то возможен случай \(a=25\).
Запишем все варианты в таблицу:
| \(a\) | \(b=100-a\) | \(S\) |
| \(1\) | \(99\) | \(99\) |
| \(2\) | \(98\) | \(196\) |
| \(4\) | \(96\) | \(384\) |
| \(5\) | \(95\) | \(475\) |
| \(8\) | \(92\) | \(736\) |
| \(10\) | \(90\) | \(900\) |
| \(16\) | \(84\) | \(1344\) |
| \(20\) | \(80\) | \(1600\) |
| \(25\) | \(75\) | \(1875\) |
| \(40\) | \(60\) | \(2400\) |
При решении этой задачи мы пользовались основной теоремой арифметики и умным перебором вариантов.