Отрезок, соединяющий середины сторон треугольника, называется средней линией треугольника.
Докажем важную теорему:
Средняя линия треугольника параллельна его третьей стороне, а длина средней линии треугольника равна половине этой стороны.
Доказательство:
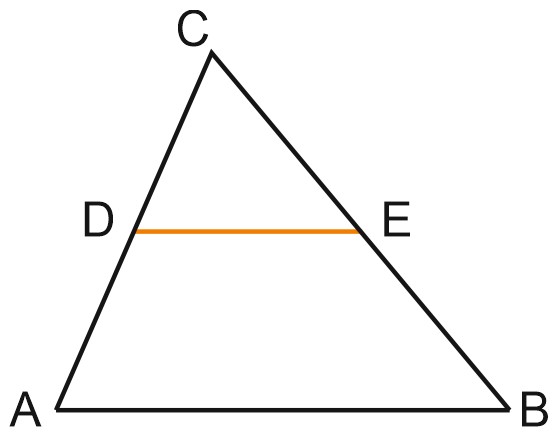
Треугольники \(ABC\) и \(DCE\) на рисунке – подобны по 2 сторонам и углу между ними. В самом деле, \(AC=2CD, \; BC=2CE,\) угол \(C\) – общий. Коэффициент подобия равен \(2\).
Тогда \(AB=2DE\), то есть \(DE\) – половина \(AB\).
Углы \(CAB\) и \(CDE\) равны. А поскольку они соответственные при прямых \(AB\) и \(DE\) и секущей \(AC\), получим, что \(AB\parallel DE\).
Чему равна площадь треугольника \(CDE\)? Отношение площадей подобных фигур равно квадрату коэффициента подобия.
В нашей задаче \(k=AB:DE=2,\)
\(\displaystyle \frac{S_{\triangle CDE}}{S_{\triangle ABC}}=k^{2}=\frac{1}{4}.\)
Средняя линия треугольника \(ABC\) отрезает от него треугольник \(CDE\), площадь которого в 4 раза меньше, чем площадь треугольника \(ABC\).
Задачи ОГЭ и ЕГЭ по теме: Средняя линия треугольника
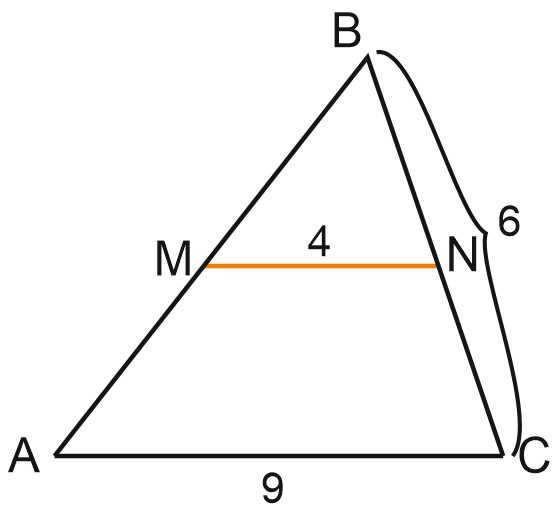
1. Через точки \(M\) и \(N\), принадлежащие сторонам \(AB\) и \(BC\) треугольника \(ABC\) соответственно, проведена прямая \(MN\), параллельная стороне \(AC\). Найдите длину \(CN\), если \(BC=6, \; MN=4, \; AC=9.\)
Решение:
1) У треугольников \(MBN\) и \(ABC\) угол \(B\) – общий.
2) Углы \(BMN\) и \(BAC\) равны, как соответственные при \(MN\parallel AC\) и секущей \(AB\).
Треугольники \(MBN\) и \(ABC\) подобны по двум сторонам.
Поэтому их стороны пропорциональны:
\(\displaystyle \frac{BN}{BC}=\frac{MN}{AC}=\frac{MB}{AB}.\)
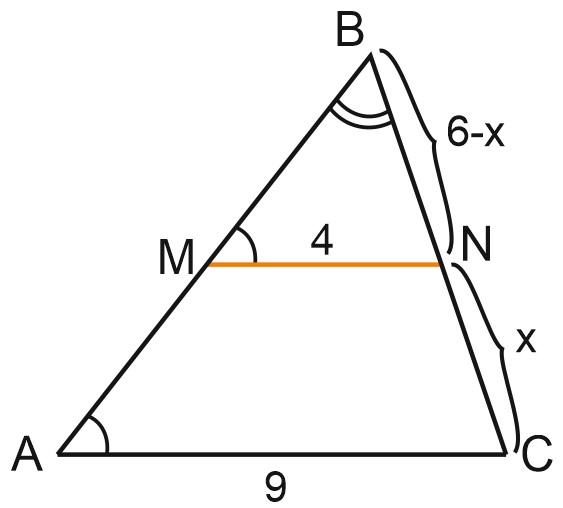
Обозначим \(NC\) за \(x\), тогда \(BN=6-x.\)
Запишем соотношение сходственных сторон:
\(\displaystyle \frac{6-x}{6}=\frac{4}{9};\)
\(9(6-x)=6\cdot 4;\)
\(x=\displaystyle \frac{10}{3}.\)
Ответ: \(\displaystyle \frac{10}{3}.\)