Анна Малкова
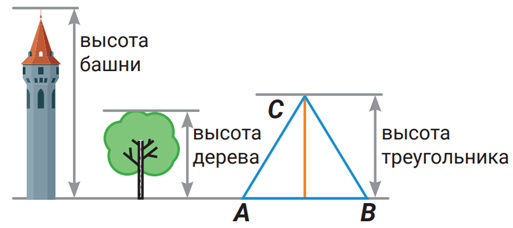
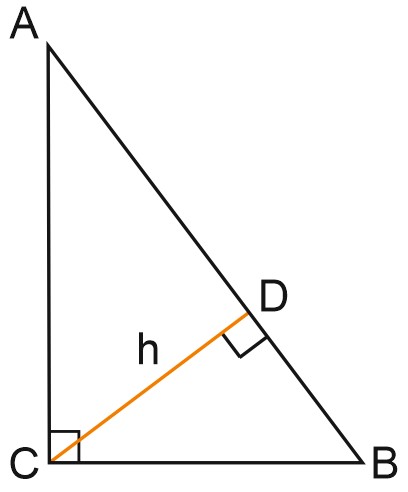
Высота треугольника – перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
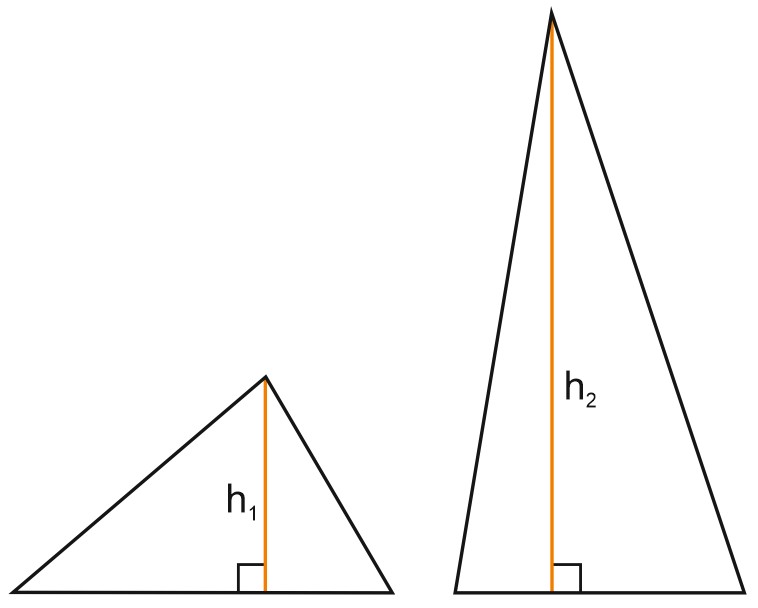
Чем больше высота, тем выше треугольник.
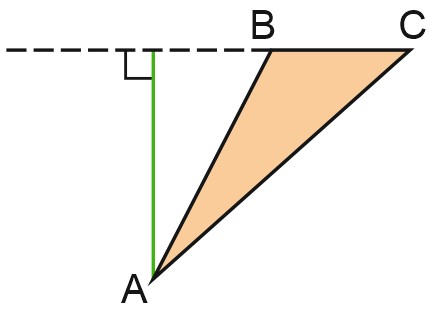
В тупоугольном треугольнике высота опускается на продолжение сторон.
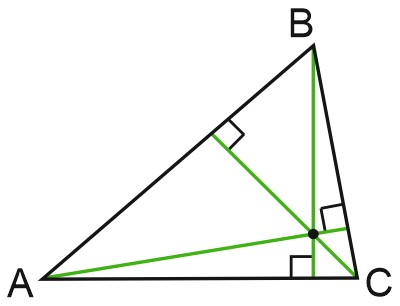
Три высоты треугольника всегда пересекаются в одной точке, которая называется ортоцентром треугольника.
В конце статьи мы докажем этот факт.
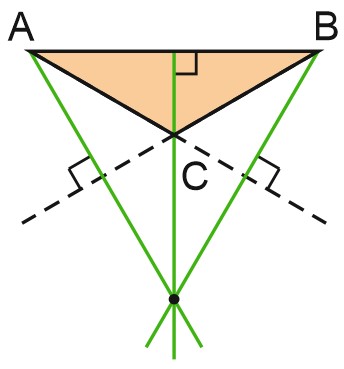
В тупоугольном треугольнике пересекаются продолжения высот.
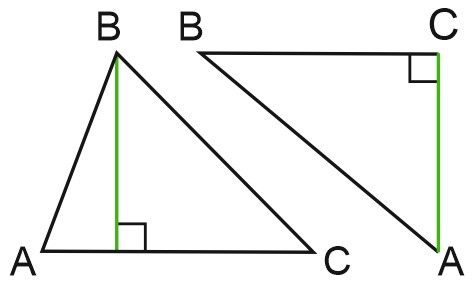
В прямоугольном треугольнике каждый катет является высотой к другому катету. Три высоты прямоугольного треугольника пересекаются в вершине прямого угла.
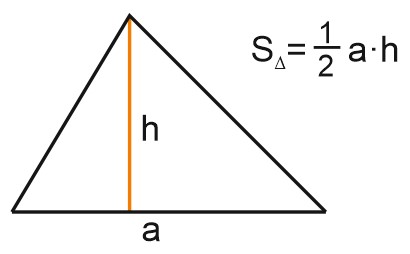
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.
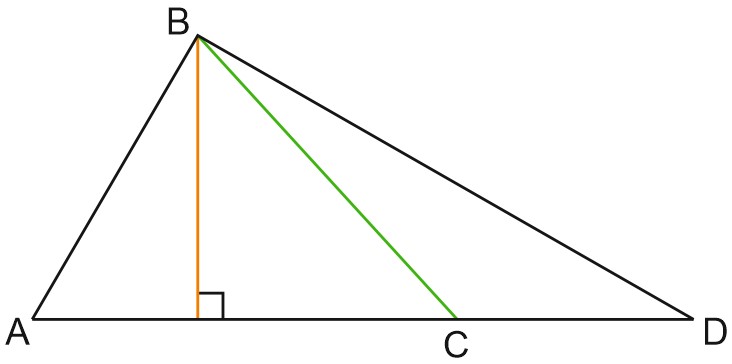
На рисунке показаны треугольники \(ABC\) и \(BCD\), имеющие общую высоту. Отношение площадей этих треугольников равно отношению \(AC\) и \(CD\):
\(\displaystyle \frac{S_{\triangle ABC}}{S_{\triangle BCD}}=\frac{AC}{CD}\)
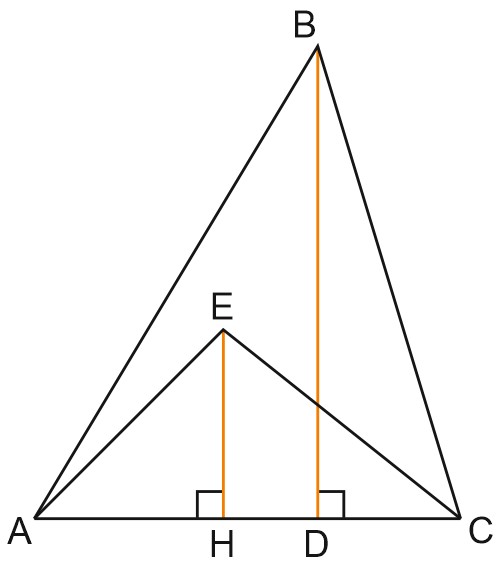
Треугольники \(ABC\) и \(AEC\) на рисунке имеют одинаковое основание и разные высоты.
Отношение площадей этих треугольников равно отношению их высот: \(\displaystyle \frac{S_{\triangle ABC}}{S_{\triangle AEC}}=\frac{BD}{EH}\).
Задачи ОГЭ и ЕГЭ по теме «Высоты треугольника»
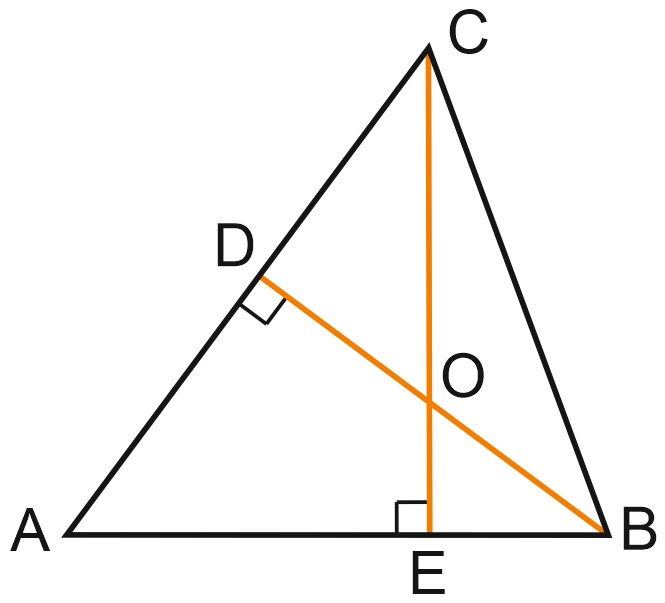
1. В остроугольном треугольнике \(ABC\) угол \(A\) равен \(65 ^{\circ}\). \(BD\) и \(CE\) — высоты, пересекающиеся в точке \(O\). Найдите угол \(DOE\). Ответ дайте в градусах.
Решение:
В треугольниках \(ACE\) и \(OCD\) угол \(C\) – общий, углы \(E\) и \(D\) равны \(90 ^{\circ}\). Значит, треугольники \(ACE\) и \(OCD\) подобны, углы \(CAE\) и \(DOC\) равны, и \(\angle DOC = 65 ^{\circ}\).
Тогда угол \(DOE\) – смежный с углом \(DOC\). Он равен \(180 ^{\circ} - 65 ^{\circ} = 115 ^{\circ}\).
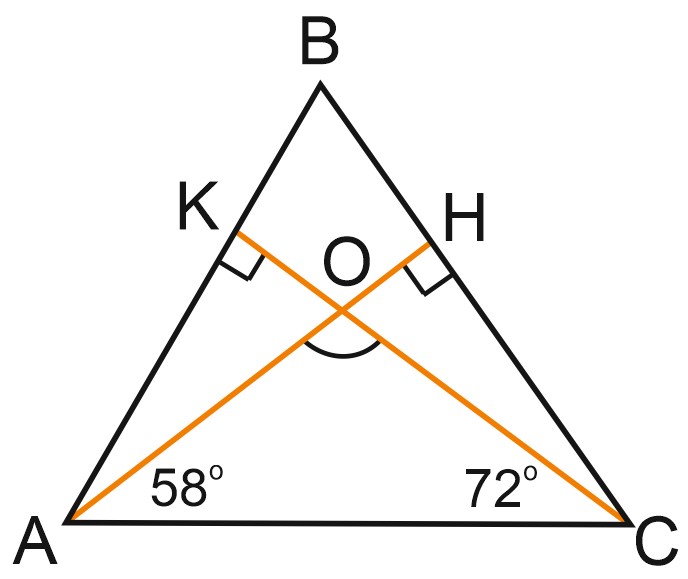
2. Два угла треугольника равны \(58 ^{\circ}\) и \(72 ^{\circ}\). Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах
Решение:
Из треугольника \(ACH\) (угол \(H\) – прямой) найдем угол \(CAH\). Он равен \(18^{\circ}\).
Из треугольника \(ACK\) (\(K\) – прямой) найдем угол \(ACK\). Он равен \(32^{\circ}\).
В треугольнике \(AOC\) известны два угла. Найдем третий, то есть угол \(AOC\), который и является тупым углом между высотами треугольника \(ABC\):
\(\angle AOC = 180^{\circ} - 18^{\circ} - 32^{\circ} = 130^{\circ}\).
Ответ: 130.
Докажем, что три высоты треугольника пересекаются в одной точке.
Пусть треугольник \(ABC\) – остроугольный.
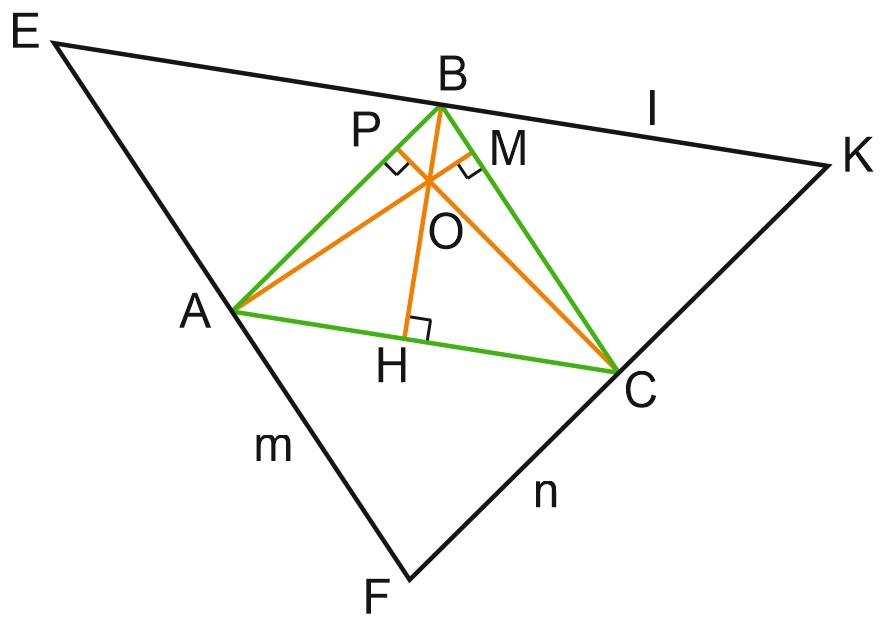
Проведем в треугольнике \(ABC\) высоты \(BH\) и \(CP\). Проведем также прямые, параллельные сторонам треугольника \(ABC\) и проходящие через вершины, противоположные этим сторонам.
\(m \parallel BC;\)
\(n \parallel AB;\)
\(l \parallel AC.\)
Заметим, что четырехугольник \(ABCF\) – параллелограмм, поскольку его противоположные стороны параллельны. Это значит, что \(CF = AB\).
Точно так же, \(ABKC\) – параллелограмм, и \(KC = AB\).
Поскольку \(AB\) и \(FK\) параллельны, \(CP\) является серединным перпендикуляром к \(FK\).
Аналогично, \(BH\) – серединный перпендикуляр к \(EK\), а \(AM\) – серединный перпендикуляр к \(EF\).
Три серединных перпендикуляра к сторонам треугольника \(EKF\) пересекаются в точке \(O\). И это значит, что три высоты треугольника \(ABC\) пересекаются в точке \(O\).
Для тупоугольного треугольника доказательство аналогично.
Точка пересечения высот треугольника называется ортоцентром и обладает замечательными свойствами.
Читайте подробнее о том, как их использовать при решении задач ЕГЭ.