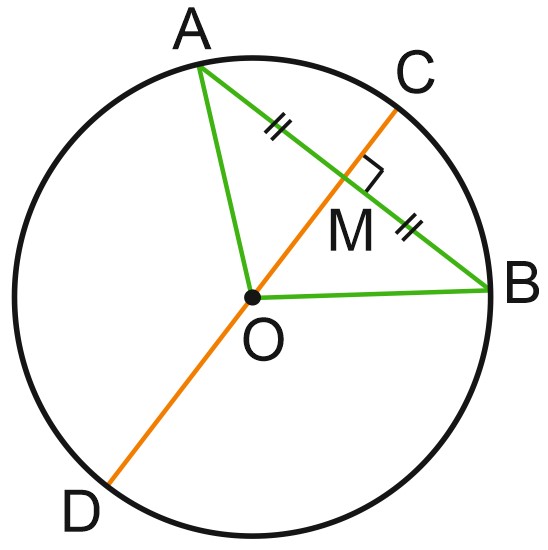
Серединный перпендикуляр к хорде проходит через центр окружности.
Серединный перпендикуляр к отрезку \(AB\) – это множество точек, равноудаленных от точек \(A\) и \(B\). Другими словами, все точки, равноудаленные от \(A\) и \(B\), лежат на серединном перпендикуляре к \(AB\).
С другой стороны, если точки \(A\) и \(B\) лежат на окружности с центром \(O\), то \(AO = BO\). Это значит, что точка \(O\) лежит на серединном перпендикуляре к \(AB\).