Четырехугольник вписан в окружность

Анна Малкова

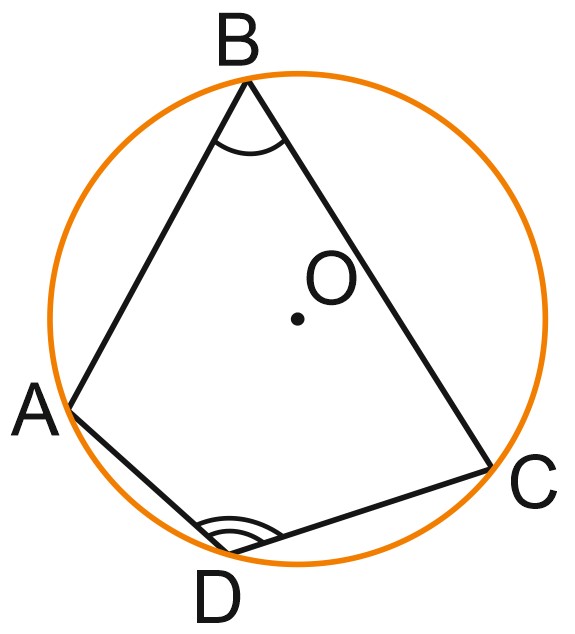
Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности.

Эта окружность будет называться описанной вокруг четырехугольника.

Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна \(180^\circ\) градусов.

\( \angle A+\angle C=\angle B+\angle D=180^{\circ}.\)

Доказательство:

Вписанные углы \(A\) и \(C\) четырехугольника \(ABCD\) на рисунке опираются на дуги \(BCD\) и \(BAD\), сумма которых равна \(360\) градусов. Значит, сумма углов \(A\) и \(C\) равна \(180^{\circ}\).

Докажем обратное утверждение.

Пусть сумма углов \(A\) и \(C\) четырехугольника \(ABCD\) равна \(180^{\circ}\). Докажем, что точки \(A, \; B, \; C\; \) и \(D\) лежат на одной окружности.

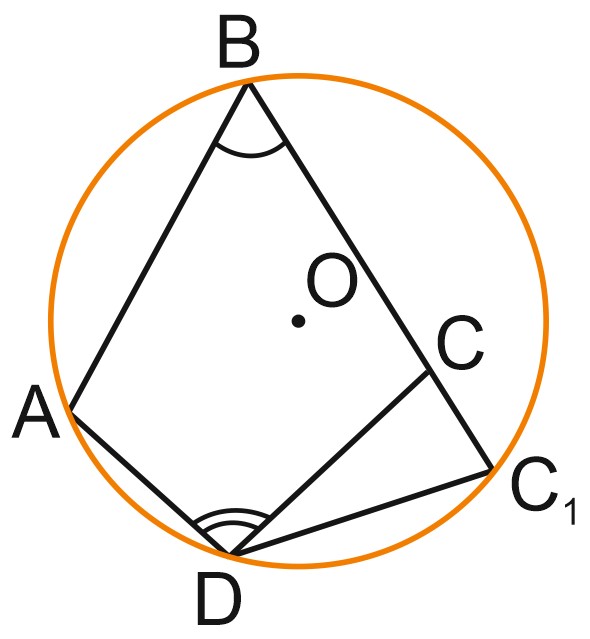
Вокруг любого треугольника можно описать окружность, причем только одну. Опишем окружность вокруг треугольника \(ABD\). Мы не знаем пока, лежит ли точка \(C\) на этой окружности. Значит, \(C\) может лежать на этой окружности, или внутри нее, или вне окружности.

Предположим, что точка \(C\) лежит внутри окружности, описанной вокруг треугольника\(ABD\). Продолжим отрезок \(BC\) до пересечения с окружностью в точке \(C_1\).

Так как четырехугольник \(ABC_1D\) вписан в окружность, сумма его противоположных углов равна \(180^{\circ}\). Это мы доказали. Значит, \(\angle BC_1D = 180^\circ - \angle BAD\).

По условию, \(\angle BCD=180^\circ - \angle BAD.\) Значит \(\angle BC_1D = \angle BCD.\)

Угол \(C_1CD\) – смежный с углом \(BCD, \; \) \(\angle C_1CD=180^\circ - \angle BCD = 180^\circ- \angle BC_1D.\)

Тогда в треугольнике \(CC_1D\) сумма углов \(C_1CD\) и \(BC_1D\) равна \(180^{\circ}\). Такой треугольник не может существовать, поскольку угол \(D\) в нем равен нулю. Значит, точка \(C\) не может лежать внутри окружности, описанной вокруг треугольника \(ABD\).

Аналогично доказывается, что \(C\) не может лежать и вне этой окружности. Остается случай, когда точки \(A, \; B, \; C\; \) и \(D\) лежат на одной окружности.

И это значит, что \(ABCD\) вписан в окружность.

1. Два угла вписанного в окружность четырёхугольника равны \(82^{\circ}\) и \(58^{\circ}\). Найдите больший из оставшихся углов. Ответ дайте в градусах.

Решение:

Сумма противоположных углов вписанного четырехугольника равна \(180^{\circ}\).

Пусть угол \(A\) равен \(82^{\circ}\). Тогда напротив него лежит угол в \(98\) градусов.

Если угол \(B\) равен \(58^{\circ}\), то угол \(D\) равен \(180^{\circ}-58^{\circ}=122^{\circ}\).

Ответ: 122.

2. Угол \(A\) четырехугольника \(ABCD\), вписанного в окружность, равен \(32^{\circ }\). Найдите угол \(C\) этого четырехугольника. Ответ дайте в градусах.

Решение:

Четырехугольник \(ABCD\) вписан в окружность. Значит, сумма его противоположных углов равна \(180^{\circ }.\)

Поэтому \( \angle C=180^{\circ } -\angle A=180^{\circ }-32^{\circ }=148^{\circ }.\)

Ответ: 148.

3. Углы \(A, \; B, \; C\) четырехугольника \(ABCD\) относятся как \(1:2:3\). Найдите угол \(D\), если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.

Решение:

Пусть \(\angle A=x, \; \angle B=2x, \; \angle C=3x, \; \angle D=y.\)

Сумма всех углов четырехугольника равна \(360^{\circ }.\)

А сумма каждой пары противоположных углов равна \(180^{\circ }\) (т. к. четырехугольник вписан в окружность).

Запишем эти два условия в виде двух уравнений с двумя неизвестными:

\(x+2x+3x+y=360;\)

\(2x+y=180. \)

Подставляем второе уравнение в первое и получаем \(4x=180, \; x=45, \; y=90^{\circ }.\)

Ответ: 90.

4. Стороны четырехугольника \(ABCD\) \(BC\) и \(CD\) стягивают дуги описанной окружности, градусные величины которых равны соответственно \(107^{\circ }\) и \(39^{\circ }\). Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Решение:

Сумма противоположных углов вписанного четырехугольника равна \(180^{\circ }\).

Поэтому \( \angle C=180^{\circ } -\angle A.\)

Угол \(A\) – вписанный, опирается на дугу \(BD\), равную сумме дуг \(BC\) и \(CD\), т. е. \(107^{\circ }+39^{\circ }=146^{\circ }.\)

Тогда вписанный угол \(A\) равен половине дуги \(BD\), т. е. \(146^{\circ }:2=73^{\circ }.\)

\( \angle C=180^{\circ } -\angle A=180^{\circ }-73^{\circ }=107^{\circ }.\)

Ответ: 107.

5. Точки \(A, \; B, \; C, \; D\), расположенные на окружности, делят эту окружность на четыре дуги \(AB, \; BC, \; CD\) и \(AD,\) градусные величины которых относятся соответственно как \(7 : 1 : 2 : 26.\) Найдите угол \(A\) четырехугольника \(ABCD.\) Ответ дайте в градусах.

Решение:

Угол \(A\) – вписанный, опирается на дугу \(BD\), равную сумме дуг \(BC\) и \(CD\). Найдем дуги \(BC\) и \(CD\).

Обозначим градусные величины дуг \(AB, \; BC, \; CD\) и \(AD\) как \(7x, \; x, \; 2x, \; 26x\) согласно заданному соотношению между дугами.

Тогда \(7x+x+2x+26x=360\) или \(36x=360, \; x=10^{\circ }.\)

Сумма дуг \(BC\) и \(CD\) составляет \(x+2x=30^{\circ }.\)

Вписанный угол \(A\) равен половине дуги \(BD\), т. е. \(30^{\circ }:2=15^{\circ }.\)

Ответ: 15.

6. Радиус окружности, описанной около квадрата, равен \(16\sqrt{2}.\) Найдите длину стороны этого квадрата.

Решение:

Радиус окружности, описанной около квадрата, равен половине диагонали квадрата.

Тогда диагональ квадрата равна \(d=2\cdot 16\sqrt{2}=32\sqrt{2}=a\sqrt{2}.\)

Выразим сторону квадрата через его диагональ: \(\displaystyle a=\frac{d}{\sqrt{2}}=32.\)

Ответ: 32.

1) Диагонали вписанного четырёхугольника разбивают его на две пары подобных треугольников.

\(\triangle AOB\sim \triangle COD, \; \triangle BOC\sim \triangle AOD.\)

2) Теорема Птолемея. Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

\(AC\cdot BD=AB\cdot CD+BC\cdot AD.\)

3) Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

4) Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

5) Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной.

Задачи ЕГЭ

7. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен \(60^{\circ }\), большее основание равно \(12\). Найдите радиус описанной окружности этой трапеции.

Решение:

Поскольку трапеция вписана в окружность, она равнобедренная.

Рассмотрим равнобедренную трапецию \(ABCD\) с основаниями \(AD=2a, \; BC=a.\)

Тогда боковые стороны \(AB=CD=a.\)

Проведем \(BO\) параллельно \(CD\). Тогда треугольник \(ABO\) – равнобедренный, т. к. \(\angle BAO = \angle AOB,\) и равносторонний, т. к. \(\angle A = 60^{\circ }.\) Поэтому \(AO=a.\)

\(BCDO\) – параллелограмм по построению, но \(BC=CD\), поэтому \(BCDO\) – ромб, и \(OD=a.\)

Получаем, что \(O\) – центр описанной окружности с радиусом, равным меньшему основанию – \(12:2 = 6.\)

Ответ: 6.

8. Найти диагональ параллелограмма, вписанного в окружность радиусом \(6\) см.

Решение:

Согласно одной из теорем, окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Прямой угол, вписанный в окружность, опирается на диаметр. Поэтому диагональ равна диаметру, \(6\cdot 2=12\) см.

Ответ: 12.

9. Около трапеции описана окружность. Периметр трапеции равен \(60\), средняя линия равна \(25\). Найдите боковую сторону трапеции.

Решение:

Средняя линия трапеции равна полусумме оснований. Поэтому сумма оснований \(AD+BC=25\cdot 2=50.\)

Сумму боковых сторон найдем как разность между периметром и суммой оснований: \(AB+CD=60-50=10.\)

Трапеция вписана в окружность, следовательно, трапеция равнобедренная, боковые стороны равны: \(AB=CD=10:2=5.\)

Ответ: 5.

10. Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны \(13\) и \(\sqrt{155}.\)

Решение:

Прямой угол, вписанный в окружность, опирается на диаметр. Поэтому диагональ равна диаметру окружности.

В то же время по теореме Пифагора диагональ найдем как \(d=\sqrt{169+155}=18.\)

Радиус окружности равен половине диаметра: \(18:2=9.\)

Ответ: 9.

11. Основания равнобедренной трапеции равны \(8\) и \(6\). Радиус описанной окружности равен \(5\). Центр окружности лежит внутри трапеции. Найдите высоту трапеции.