previous arrow
next arrow
Slider
Центр подготовки к ЕГЭ > Материалы для подготовки к ЕГЭ и ОГЭ > Диаметр, перпендикулярный хорде, делит ее пополам

Диаметр, перпендикулярный хорде, делит ее пополам

Анна Малкова

Доказательство:

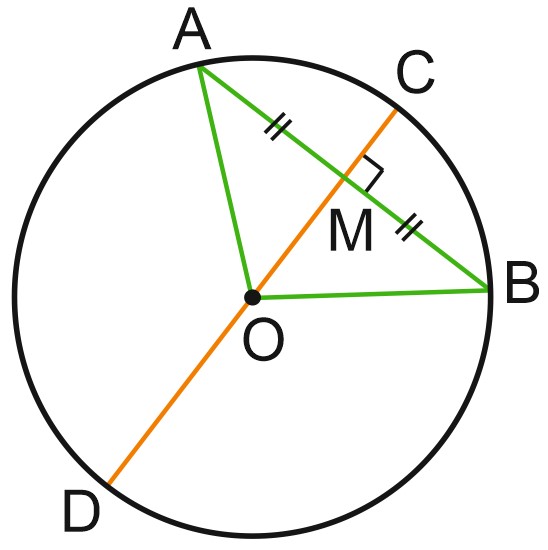
Пусть АВ – хорда окружности, CD – перпендикулярный ей диаметр, пересекающий АВ в точке М. Треугольник ОАВ – равнобедренный, АО = ОВ как радиусы окружности. Тогда его высота ОМ является также и медианой, М – середина АВ.

 

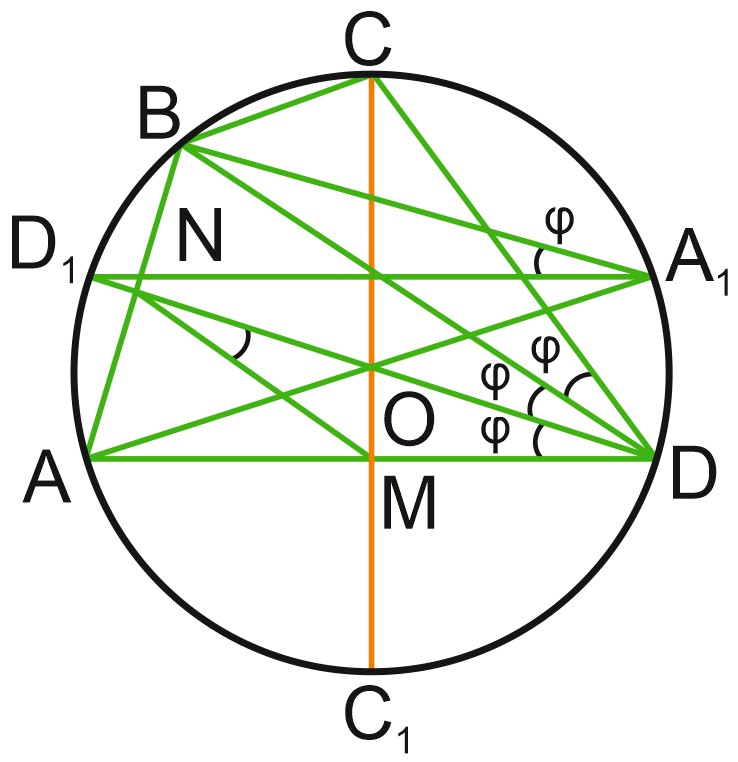
1. Четырёхугольник АВСD вписан в окружность. Диаметр CC1 перпендикулярен стороне AD и пересекает её в точке М, а диаметр DD1 перпендикулярен стороне AB и пересекает её в точке N.

а) Пусть АА1 также диаметр окружности. Докажите, что углы DNM и BA1D1 равны.

б) Найдите углы четырёхугольника ABCD, если угол CDB вдвое меньше угла ADB.

 

а) Докажем:
\angle DNM = \angle BA_1D_1.

Диаметр, перпендикулярный хорде, делит ее пополам, поэтому N – середина АВ, М – середина АD.

Рассмотрим  \triangle BAD; \,  \, MN – средняя линия \triangle BAD; \, \, MN\parallel BD. Значит, D_1DB=\angle MND (накрест лежащие) \angle D_1DB=\angle D_1A_1B – вписанные, опираются на одну дугу.

б) Найдем углы четырехугольника ABCD, если  2\angle CDB=\angle ADB

Пусть \angle CDB=\varphi , тогда \angle ADB=2\varphi =2\angle BDD_1. Треугольник ABD – равнобедренный, поскольку медиана DN является его высотой. Значит, \angle ADC=3\varphi . Тогда \angle DC_1 M=90^{\circ}-3\varphi  (из треугольника DC_1 M).

\angle DOC_1=2\angle DC_1 M= 180^{\circ}-6\varphi  – как центральный угол, опирающийся на ту же дугу.

Рассмотрим \triangle DOM. В этом треугольнике:

180^{\circ}-6\varphi +\varphi =90^{\circ}, отсюда \varphi =18^{\circ}.

Тогда \angle D=3\varphi =54^{\circ}, \, \, \angle ABC=180^{\circ}-3\varphi =126^{\circ} – по свойству четырехугольника, вписанного в окружность.

Из \triangle  AND:\, \, \angle A=90^{\circ}-\varphi =72^{\circ}, тогда \angle BCD=180^{\circ}-\angle A= 108^{\circ}.

Мы нашли все углы четырехугольника ABCD.

 

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Диаметр, перпендикулярный хорде, делит ее пополам» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 08.03.2023