«Классические» схемы для решения задач ЕГЭ по геометрии

Перед вами – полезные схемы, по которым строится множество задач ЕГЭ по геометрии (Задача 16 на ЕГЭ по математике). И если что-то подобное вы увидели в задаче – вам очень повезло!
Чтобы решить задачу 16 ЕГЭ по математике легко и правильно, заранее докажите указанные здесь утверждения. Возможно, что-то похожее встретится вам на ЕГЭ!

Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК

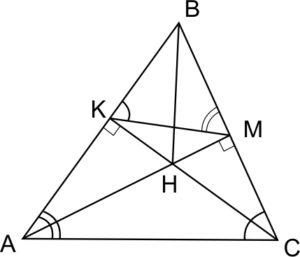
1) △МВК ~△АВС, k=|cos⁡В |
2) Четырехугольник АКМС можно вписать в окружность.
3) Четырехугольник ВКМН можно вписать в окружность.
4) Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
5) ВН = 2R|cos В |, где R – радиус описанной окружности △АВС.

Схема 2. Пусть луч МА пересекает окружность в точках А и В, а луч МD – в точках С и D, причем МА > МВ, МD > МС. Тогда треугольники ВМС и DМА подобны.

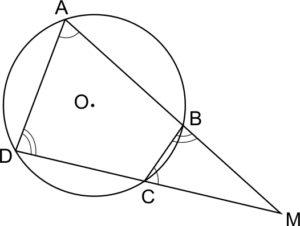
Схема 3. У треугольников АВС и АМС сторона АС – общая, угол В равен углу М. Тогда точки А, В, С, М лежат на одной окружности.

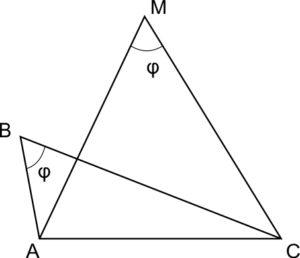
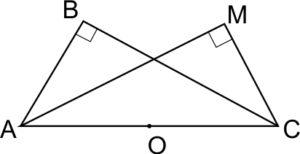
Схема 4. У треугольников АВС и АМС сторона АС – общая, углы В и М – прямые. Тогда точки А, В, С, М лежат на окружности, радиус которой равен половине АС.