Анна Малкова
Пусть \(P\) – центр вписанной окружности треугольника \(ABC, \; Q\) – центр его вневписанной окружности, касающейся стороны \(BC\).
Точка пересечения биссектрисы угла \(A\) треугольника \(ABC\) с его описанной окружностью равноудалена от точек \(B, \; C, \; P, \; Q\). Эта схема называется также теоремой о трилистнике.
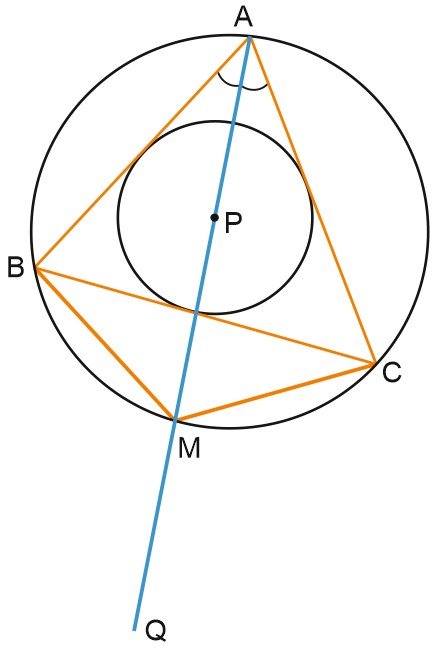
Дан треугольник \(ABC, \; AM\) – биссектриса угла \(A, \; P\) – центр вписанной окружности треугольника \(ABC, \; Q\) – центр его вневписанной окружности (которая касается стороны \(BC\) и продолжений сторон \(AB\) и \(AC\)), \(M\) – точка пересечения биссектрисы угла А и описанной окружности треугольника \(ABC\). Докажем, что \(MP = MB = MC.\)
Видите на рисунке «трезубец» (или «трилистник»), состоящий из отрезков \(MP, \; MB, \; MC, \; MQ\)?
Докажем сначала, что \(MB = MC = MP.\)
Вписанные углы \(BAM\) и \(BCM\) опираются на дугу \(BM\), следовательно, они равны.
Аналогично, вписанные углы \(CAM\) и \(CBM\) опираются на дугу \(CM\), и они тоже равны.
\( \angle BAM=\angle CAM\), поскольку \(AM\) – биссектриса угла \(BAC\).
Следовательно, \(\angle BCM=\angle BAM=\angle CAM=\angle CBM= \alpha\) и треугольник \(BMC\) – равнобедренный, \(BM = CM.\)
Точка \(P\) – центр вписанной окружности треугольника \(ABC\). Значит, \(P\) – точка пересечения биссектрис треугольника \(ABC\), и тогда \(BP\) и \(CP\) – биссектрисы его углов \(ABC\) и \(ACB\) соответственно.
Пусть \(\angle BAC=2\alpha, \; \angle ABC=2\beta , \; \angle ACB=2\gamma.\)
Сумма углов треугольника \(ABC\) равна \(180^{\circ}\), значит, \( 2\alpha +2\beta +2\gamma =180^{\circ}.\)
В треугольнике \(BMP\):
\(\angle PMB=\angle ACB=2\gamma ,\)
\( \angle PBM=\alpha+\beta .\)
Тогда \( \angle BPM=\alpha+\beta=\angle PBM\), треугольник \(BMP\) равнобедренный, \(BM = PM\). Значит, точка \(M\) равноудалена от точек \(B, \; C\) и \(P\). Аналогично доказывается, что \(MQ = BM = CM = PM.\)
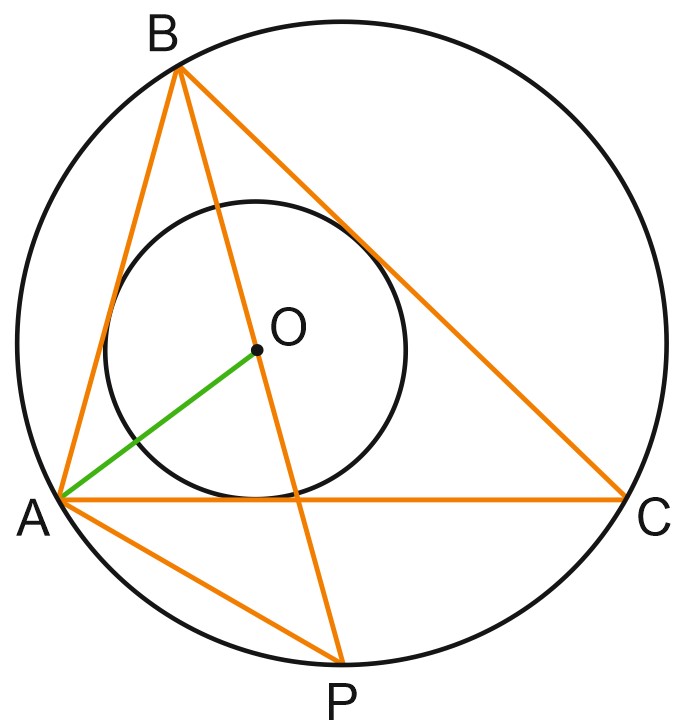
1. Точка \(O\) – центр вписанной в треугольник \(ABC\) окружности. Прямая \(BO\) вторично пересекает описанную около этого треугольника окружность в точке \(P\).
а) Докажите, что \(\angle POA=\angle PAO.\)
б) Найдите площадь треугольника \(APO\), если радиус описанной около треугольника \(ABC\) окружности равен \(6, \; \angle BAC=75^{\circ}, \; \angle ABC=60^{\circ}.\)
Решение:
В этой задаче, как и в лемме о трезубце, биссектриса треугольника пересекает описанную вокруг него окружность. Пункт (а) доказываем так же, как доказывали лемму о трезубце.
а) Так как \(O\) – центр вписанной в \(\triangle ABC\) окружности, то \(AO\) и \(BO\) – биссектрисы.
Введем обозначения: \(\angle BAO=\alpha , \; \angle ABO=\beta .\)
Следовательно, по теореме о внешнем угле имеем: \(\angle AOP=\alpha + \beta.\)
Углы \(\beta=\angle CBP=\angle CAP\) как вписанные, опирающиеся на одну и ту же дугу.
Следовательно, \(\angle PAO=\alpha + \beta= \angle AOP.\)
Что и требовалось доказать.
б) Пусть \(R\) – радиус описанной около \(\triangle ABC\) окружности. Тогда по теореме синусов для \(\triangle ABP\):
\(\displaystyle \frac{AP}{sin\angle ABP}=2R\Rightarrow AP=2Rsin30^{\circ}=6.\)
Следовательно, \(OP=AP=6.\)
Далее имеем: \(\angle APO=180^{\circ}-2\left(\displaystyle \frac{75^{\circ}}{2}+30^{\circ}\right)=45^{\circ}.\)
Следовательно, искомая площадь равна:
\(S_{APO}=\displaystyle \frac{1}{2}\cdot AP\cdot OP\cdot sin45^{\circ}=9\sqrt{2}.\)
Ответ: \(9\sqrt{2}.\)