Радиус окружности, вписанной в прямоугольный треугольник с катетами а и b и гипотенузой с, равен [math]\frac{1}{2}(a+b-c)[/math]

Анна Малкова

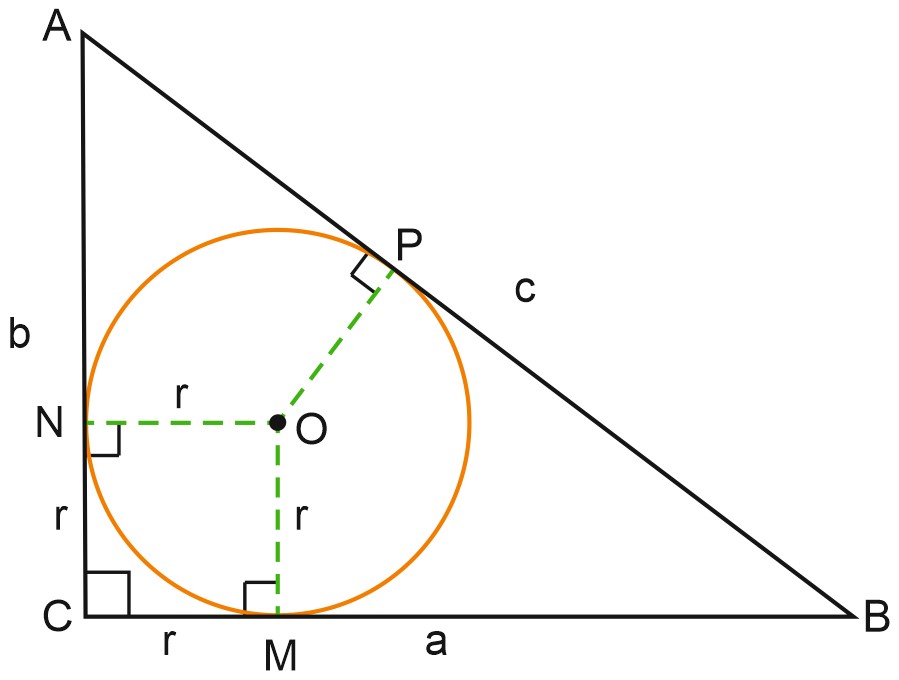
Рассмотрим прямоугольный треугольник ABC (угол C – прямой), в который вписана окружность с центром в точке O и радиусом r. Катеты AC=b,BC=a, гипотенуза AB=c. Надо доказать, что $r=\frac{a+b-c}{2}$ .

Вспомним, что отрезки касательных к окружности, проведенные из одной точки, равны.
Проведем $OM \perp a, ON \perp b, OP \perp c.$
Смежные стороны четырехугольника CMON равны (ON=OM=r), все углы прямые $\left ( \angle C = \angle N = \angle M = 90 ^{\circ} \right )$ , значит, CMON – квадрат.

Тогда NC=CM=r, AN=AP=b-r (по свойству длин отрезков касательных); аналогично BM=BP=a-r.
Поскольку АВ = АР + ВР, получим:
$c=b-r+a-r$ , отсюда
$r=\frac{a+b-c}{2}$ .

Задача ЕГЭ по теме «Радиус окружности, вписанной в прямоугольный треугольник»

Катеты равнобедренного прямоугольного треугольника равны $82+41 \sqrt{2}$ . Найдите радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в прямоугольный треугольник: $r=\frac{a+b-c}{2}$ . Гипотенуза равнобедренного прямоугольного треугольника в $\sqrt{2}$ раз больше катета. Получим:

$r=\frac{a+b-c}{2}=\frac{2(82+41\sqrt{2})-\sqrt{2}(82+41\sqrt{2})}{2}=$

$=\frac{164+82\sqrt{2}-82\sqrt{2}-82}{2}=\frac{82}{2}=41$

Ответ: 41.

Радиус окружности, вписанной в прямоугольный треугольник с катетами а и b и гипотенузой с, равен $\frac{1}{2}(a+b-c)$

Это полезно