Анна Малкова
Равные хорды удалены от центра окружности на равные расстояния.
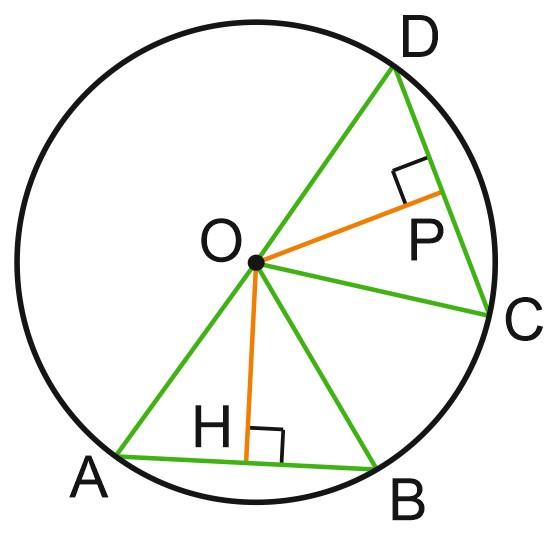
Пусть \(AB\) и \(CD\) – равные хорды одной окружности. Тогда \(OA = OB= OC =OD\) как радиусы окружности и треугольники \(AOB\) и \(COD\) равны по трем сторонам.
Это значит, что высоты этих треугольников \(OH\) и \(OP\) равны. Значит, хорды \(AB\) и \(CD\) удалены от центра окружности на равные расстояния.