Свойства высот треугольника. Ортоцентр

Анна Малкова

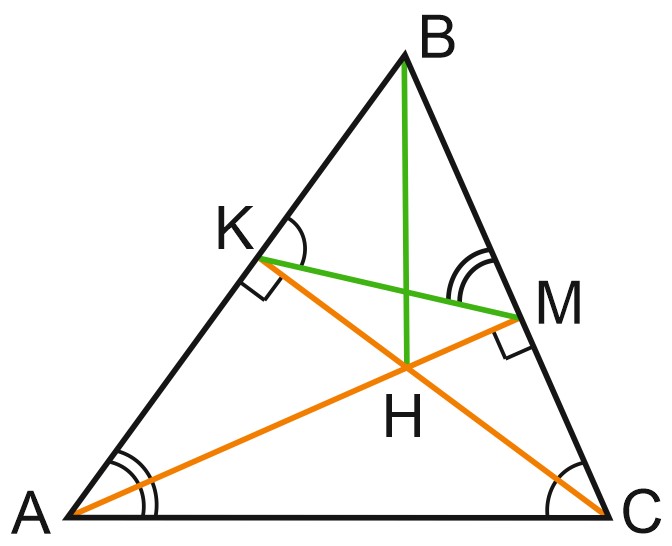
Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК

Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.

1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
$k=cosB$ , если , и , если

Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
Четырехугольник ВКМН также можно вписать в окружность.
Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
$BH=2R\left | cosB \right |$ ,где R – радиус описанной окружности $\triangle ABC$ .

Докажем эти факты по порядку.

1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам

$\triangle ABM \sim \triangle CBK\Rightarrow \frac{BM}{BK}=\frac{AB}{BC}\Rightarrow \frac{BM}{AB}=\frac{BK}{BC}.$

Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что $\triangle MBK \sim \triangle ABC$ по углу и двум сторонам.

2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны $180 ^{\circ}$ .

Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
$\angle ACB= \angle BKM=\gamma$ – как смежный с углом ВКМ. Получили, что $\angle AKM = 180 ^{\circ} - \angle BKM=180 ^{\circ} - \gamma$ , и это значит, что четырехугольник AKMC можно вписать в окружность.

3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН - прямые, их сумма равна $180 ^{\circ}$ , и значит, четырехугольник КВМН можно вписать в окружность.

4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,
$R_{\triangle ABC}=\frac{AC}{2sin \angle ABC}.$
Радиус окружности, описанной вокруг треугольника АНС, $R_{\triangle AHC}=\frac{AC}{2sin \angle AHC}.$
Мы помним, что $sin\left ( 180 ^{\circ}-\alpha \right )=sin\alpha$ . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.

5) Докажем, что $BH=2R\left | cosB \right |$ ,где R – радиус описанной окружности $\triangle ABC$ . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, $BH=\frac{MK}{sin \angle ABC}.$ .

Диаметр окружности, описанной вокруг треугольника АВС, равен $\frac{AC}{sin \angle ABC}.$ Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно $\left | cosB \right |$ . Получили, что $BH=2R\left | cosB \right |.$

Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)

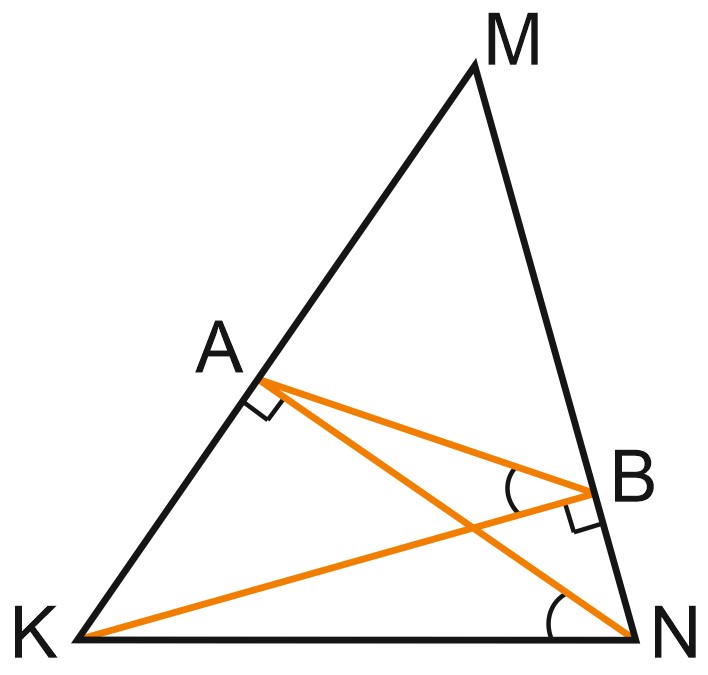
2. В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что $KN=8\sqrt{2}$ и $\angle KMN=45{^\circ }$

а) Докажем, что $\angle ABK=\angle ANK.$
$\triangle MBK \sim \triangle MAN$ (по двум углам). Запишем отношение сходственных сторон: $\frac{MA}{MB}=\frac{MN}{MK}.$
Но это значит, что $\triangle ABM\sim \triangle NKM$ (по углу и двум сторонам), причем $k=\frac{MA}{MN}=cos\angle KMN$ .

$\angle MAB=\angle MNK,\angle BAK-$ - смежный с углом $\angle MAB$ ,
$\angle BAK = 180 ^{\circ} - \angle MAB = 180 ^{\circ} - \angle BNK$ ,
$\angle BAK+\angle BNK = 180 ^{\circ},$ ,четырехугольник ABNK можно вписать в окружность.
$\angle ABK=\angle ANK$ (опираются на одну дугу).

б) Найдем $R_{\triangle ABM}$ , если $KN=8\sqrt{2}$ и $\angle KMN=45 ^{\circ}$
$\triangle ABM \sim \triangle NKM, k=cos \angle KMN=\frac{\sqrt{2}}{2};$
$\frac{AB}{KN}=k,\: \: \: AB=\frac{\sqrt{2}}{2}\cdot KN=\frac{\sqrt{2}}{2}\cdot 8\sqrt{2}=8.$
По теореме синусов,

$R_{\triangle ABM}=\frac{AB}{2sin \angle AMB}=\frac{8\cdot 2}{2\cdot \sqrt{2}}=4\sqrt{2}.$

Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Свойства высот треугольника. Ортоцентр» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 09.03.2023

Это полезно