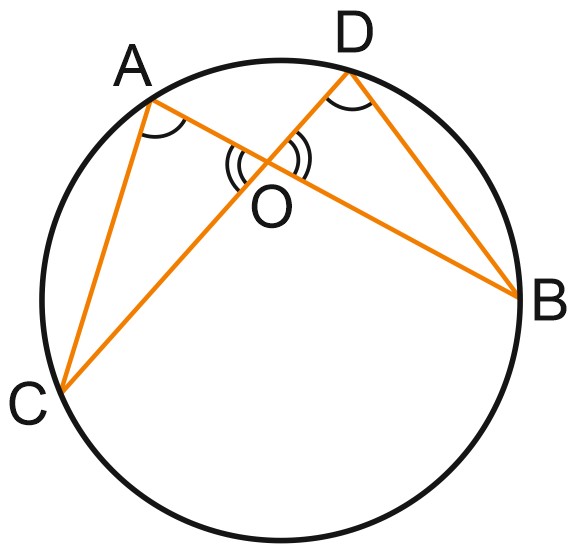
Теорема о пересекающихся хордах. Произведения отрезков пересекающихся хорд окружности равны.
Докажем, что \(AO \cdot BO=CO \cdot DO\).
Рассмотрим треугольники \(AOC\) и \(DOB\).
\(\angle AOC = \angle DOB\) (вертикальные);
\(\angle CAB = \angle CDB\) (как опирающиеся на дугу \(BC\)).
\(\triangle AOC \sim \triangle DOB\) (по двум углам).
Отсюда \(\displaystyle \frac{AO}{OD}=\frac{CO}{OB}\Rightarrow AO \cdot OB=OC \cdot OD\) – что и требовалось доказать.