Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
Доказательство:
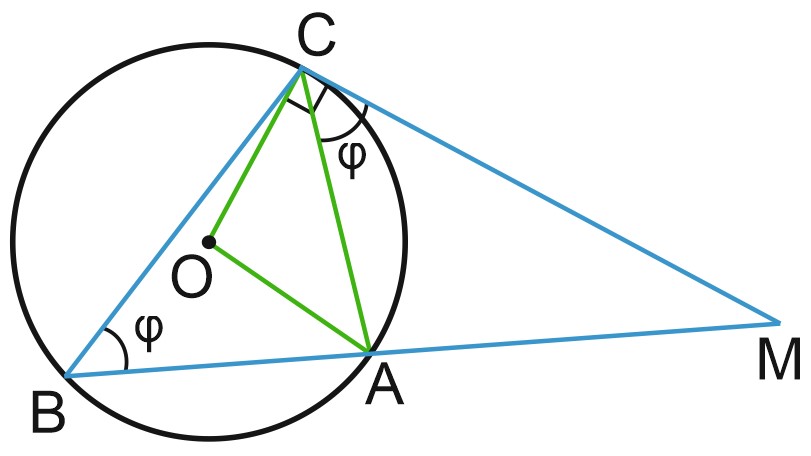
Касательная перпендикулярна радиусу, проведенному в точку касания.
Пусть \(\angle MCA=\varphi\). Тогда \(\angle OCA = 90 ^{\circ}-\varphi\).
Треугольник \(OCA\) – равнобедренный, \(OA = OC\) (как радиусы окружности).
Значит, \(\angle AOC= 180 ^{\circ}-2\left ( 90 ^{\circ} - \varphi \right )=2\varphi\), что и требовалось доказать.
Заметим, что \(\angle ABC = \varphi\) – как вписанный, опирающийся на ту же дугу.
Задача ЕГЭ по теме «Угол между касательной и хордой»
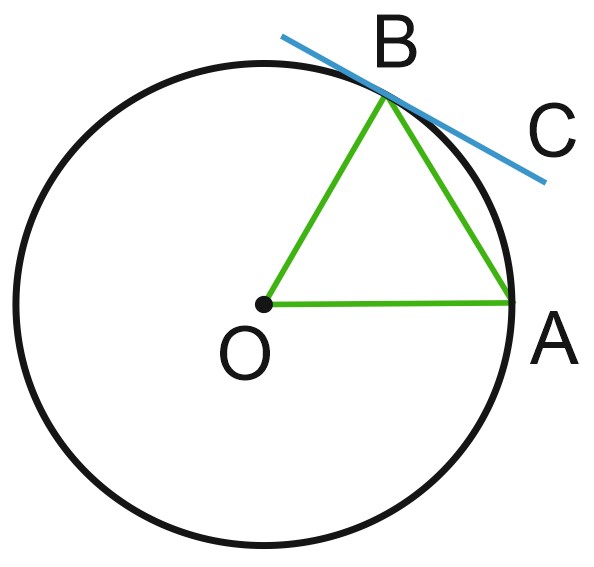
1. Угол между хордой \(AB\) и касательной \(BC\) к окружности равен \(32 ^{\circ}\). Найдите величину меньшей дуги, стягиваемой хордой \(AB\). Ответ дайте в градусах.
Решение:
Касательная \(BC\) перпендикулярна радиусу \(OB\), проведенному в точку касания. Значит, угол \(OBC\) равен \(90 ^{\circ}\), и тогда угол \(OBA\) равен \(90 ^{\circ} - 32 ^{\circ} = 58 ^{\circ}\).
Угол \(OAB\) также равен \(58 ^{\circ}\), так как треугольник \(OAB\) – равнобедренный, его стороны \(OA\) и \(OB\) равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол \(AOB\), равен \(180 ^{\circ} - 58 ^{\circ} \cdot 2 = 64 ^{\circ}\).
Центральный угол равен угловой величине дуги, на которую он опирается, и тогда дуга \(AB\) равна \(64 ^{\circ}\).
Эту задачу можно решить быстрее, зная теорему об угле между касательной и хордой.
Угол между касательной и хордой, проведенной через точку касания, - это угол \(ABC\). Он равен половине угловой величины дуги, заключенной между касательной \(BC\) и хордой \(AB\), то есть дуги \(AB\).
Значит, дуга \(AB\) равна \(64 ^{\circ}\).
Ответ: 64.