Анна Малкова
Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
Доказательство:
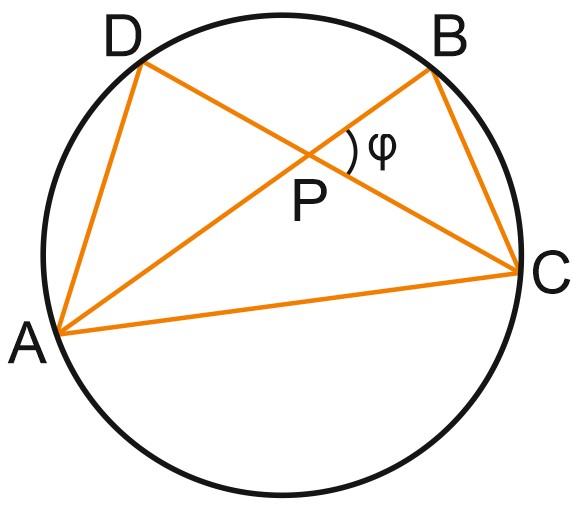
Пусть \(AB\) и \(CD\) – пересекающиеся хорды. Покажем, что угол между ними \(\varphi=\displaystyle \frac{\breve{AD}+\breve{BC}}{2}\).
Пусть хорды \(AB\) и \(CD\) пересекаются в точке \(P\).
Вписанный угол \(ACD\) опирается на дугу \(AD\) и равен ее половине.
Вписанный угол \(BAC\) опирается на дугу \(BC\) и равен ее половине.
Угол \(\varphi\) – внешний угол треугольника \(APC\). Он равен сумме внутренних углов, не смежных с ним: \(\varphi=\displaystyle \frac{\breve{AD}+\breve{BC}}{2}.\)