Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
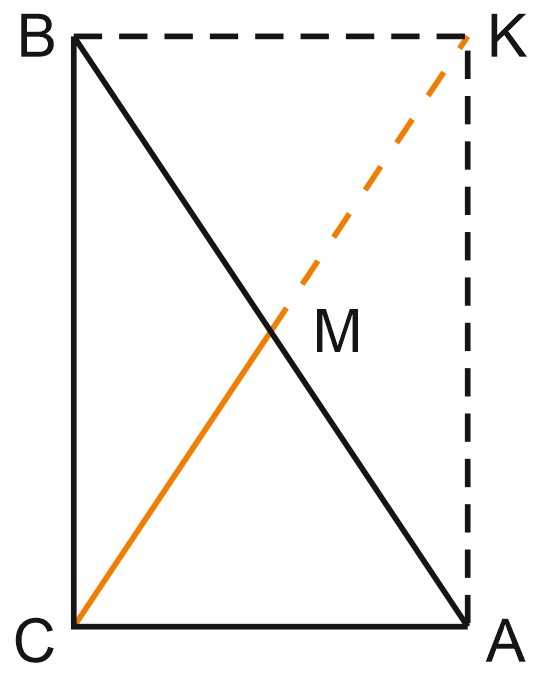
Пусть \(CM\) – медиана прямоугольного треугольника \(ABC\) с прямым углом \(C\).
Продлим \(CM\) за точку \(M\) и отметим на луче \(CM\) точку \(K\) так, что \(CM = MK\).
Треугольники \(BKM\) и \(ACM\) равны по углу и двум сторонам. Значит, углы \(BKM\) и \(ACM\) равны (накрест лежащие), тогда \(BK\) параллельна \(AC\) и \(BK = AC, \; AKBC\) – параллелограмм, причем угол \(C\) в нем – прямой.
Мы получили прямоугольник \(AKBC\).
Диагонали прямоугольника равны и в точке пересечения делятся пополам.
Значит, \(CM=AM=BM=\displaystyle \frac{1}{2}AB\).
Задача ЕГЭ по теме «Медиана прямоугольного треугольника»
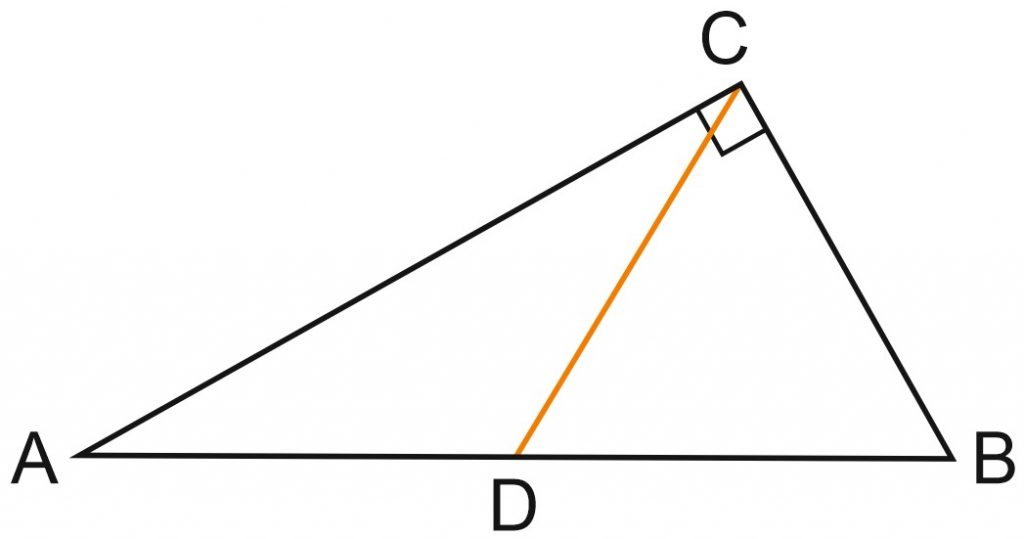
В треугольнике \(ABC\) угол \(ACB\) равен \(90 ^{\circ}\), угол \(B\) равен \(58 ^{\circ}\), \(CD\) – медиана. Найдите угол \(ACD\). Ответ дайте в градусах.
Решение:
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник \(CBD\) – равнобедренный, \(CD = BD\). Тогда
\(\angle DCB = \angle DBC = 58 ^{\circ}\).
Углы \(ACD\) и \(DCB\) в сумме дают \(90 ^{\circ}\). Отсюда
\(\angle ACD = 90 ^{\circ} - \angle DCB = 90 ^{\circ} - 58 ^{\circ} = 32 ^{\circ}\).