Метод областей применяется для решения неравенств с двумя переменными. Можно сказать, что это двумерный аналог метода интервалов.
1. Анна Малкова. При каких значении параметра \(a\) система уравнений
\(\left\{\begin{matrix}
x^2+y^2\leq x^2\cdot y^2+1, \\
x^2+y^2\leq 2, \\
(x-a)^2+(y-a)^2=|a|\end{matrix}\right.\) имеет единственное решение?
Решение:
Заметим, что параметр в этой системе есть только в третьем уравнении. А в неравенствах – ни в первом, ни во втором – его нет.
Начнем с первого неравенства. Разложим его левую часть на множители.
\(x^2y^2-x^2-y^2+1\geq 0;\)
\(x^2(y^2-1)-(y^2-1)\geq 0;\)
\((x^2-1)(y^2-1)\geq 0;\)
\((x-1)(x+1)(y-1)(y+1)\geq 0.\)
Это рациональное неравенство. Если бы в нем была одна переменная, например, только \(x\), мы решали бы его методом интервалов. Но в нем две переменных.
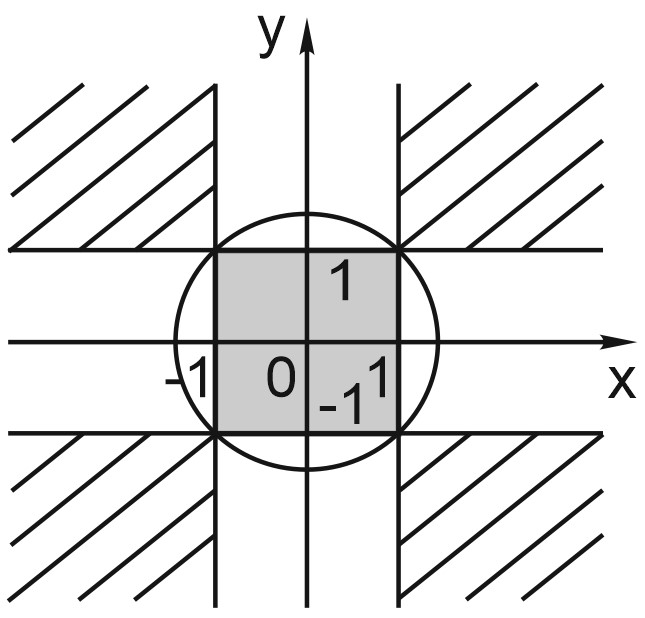
Для неравенств такого вида применяется метод областей – двумерный аналог метода интервалов. Решим неравенство \((x-1)(x+1)(y-1)(y+1)\geq 0\) методом областей.
Изобразим на координатной плоскости \((x; y)\) прямые \(x=1\), \(x=-1\), \(y=1\) и \(y=-1\).
Эти прямые разбивают координатную плоскость на области, в каждой из которых выражение в левой части неравенства сохраняет свой знак (либо оно положительно, либо отрицательно).
Прямые \(x=1\), \(x=-1\), \(y=1\) и \(y=-1\) являются границами областей.
При переходе через границу области выражение \((x-1)(x+1)(y-1)(y+1)\) меняет знак. Например, если слева от прямой \(x=1\) выполняется условие \(x < 1\). Справа от этой прямой \(x > 1\), одна из скобок поменяла знак, и вместе с ней знак всего выражения поменялся на противоположный.
Все как в методе интервалов! Только вместо точек – линии, вместо интервалов – области. Потому что переменная не одна, а две.
Проверим знаки выражения \((x-1)(x+1)(y-1)(y+1)\) в каждой из областей.
Для точки \((0; 0)\) неравенство выполняется, \((x-1)(x+1)(y-1)(y+1) > 0\).
Для точки \((0;2)\) – не выполняется.
Мы можем проверять знак выражения \((x-1)(x+1)(y-1)(y+1)\) и в других точках координатной плоскости. Или просто менять знак при переходе через каждую из границ. Закрашенные области на рисунке соответствуют областям, где неравенство выполняется.
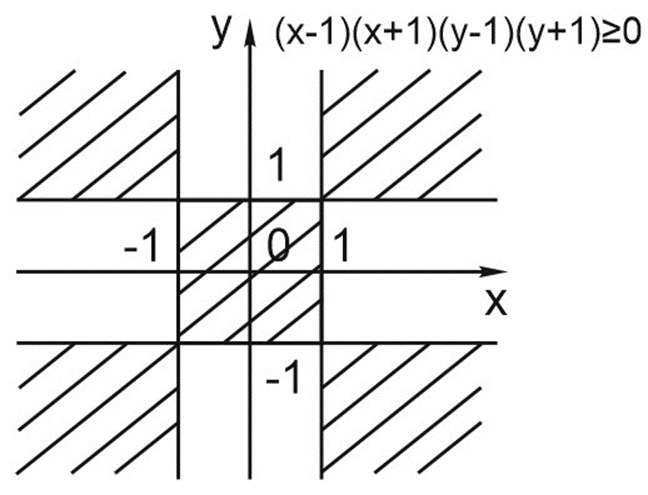
Нарисуем область, заданную вторым неравенством системы:
\(x^2+y^2\leq 2.\)
На координатной плоскости это неравенство задает круг с центром в начале координат и радиусом \(\sqrt{2}\). Обратите внимание, что точки \((1; 1); (-1; 1); (1; -1)\) и \((-1; -1)\) лежат на окружности \(x^2+y^2=2\).
Совместим решения первого и второго неравенств.
Уравнение \((x-a)^2+(y-a)^2=|a|\) задает окружность радиуса \(\sqrt{|a|}\) с центром в точке \((a; a)\).
Это значит, что ее центр лежит на прямой \(y=x\).
Параметр \(a\) может быть положительным или отрицательным. Он может быть также равным нулю, и решением будет точка \((0; 0)\). Тогда исходная система имеет единственное значение, поскольку точка \((0;0)\) лежит внутри квадрата, задаваемого первым и вторым неравенствами.
Исходная система также имеет единственное решение, если окружность, задаваемая третьим уравнением, проходит через точку \(A\) или точку \(B\) на рисунке. Во всех остальных случаях система не имеет решений или имеет более одного решения.
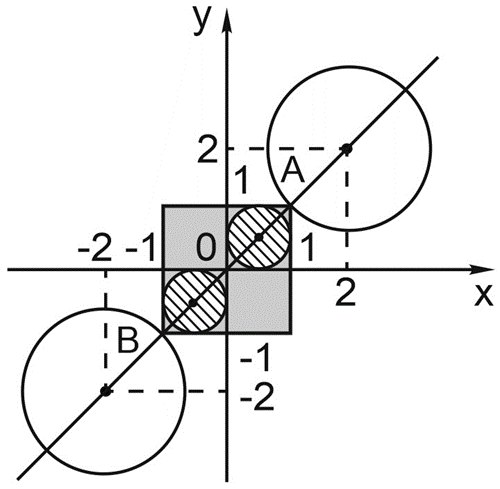
Найдем, при каких значениях параметра задаваемая третьим уравнением окружность проходит через точку \(A\) или через точку \(B\).
1) Подставим координаты точки \(A(1;1)\) в третье уравнение:
\(\left\{\begin{matrix}
2(a-1)^2=|a|,\\
a > 0.\end{matrix}\right.\)
Условие \(a>0\) добавлено потому, что центр окружности расположен дальше от начала координат, чем точка \(A\). Значит, обе координаты центра окружности положительны.
При \(a>0\) имеем: \(|a|=a\) и \(\left\{\begin{matrix}
2(a-1)^2=a, \\
a > 0.\end{matrix}\right.\)
Решения системы: \(a=2\) и \(a=\displaystyle \frac{1}{2}\).
Но если \(a=\displaystyle \frac{1}{2}\), центр окружности лежит внутри квадрата и система имеет бесконечно много решений. Значит, единственное решение будет при \(a=2\).
2) Подставим координаты точки \(B\) в уравнение окружности:
\(\left\{\begin{matrix}
2(a+1)^2=|a|, \\
a < 0;\end{matrix}\right.\)
\(\left[\begin{matrix}
a=-2, \\
a=-\displaystyle \frac{1}{2}.\end{matrix}\right.\)
Второе значение нам не подходит – как и в предыдущем пункте.
Исходная система имеет единственное решение, если \(a=-2\).
Ответ: \(-2; 0; 2\).
2. Найдите все значения параметра \(a\), при каждом из которых система
\(\left\{\begin{matrix}
(y+2x)(2y+x)\leq 0, \\
\sqrt{(x-a)^2+(y-a)^2}=\displaystyle \frac{|a+1|}{\sqrt{5}}\end{matrix}\right. \begin{matrix}
\; (1) \\
\; (2)\end{matrix}\) имеет ровно два решения.
Решение:
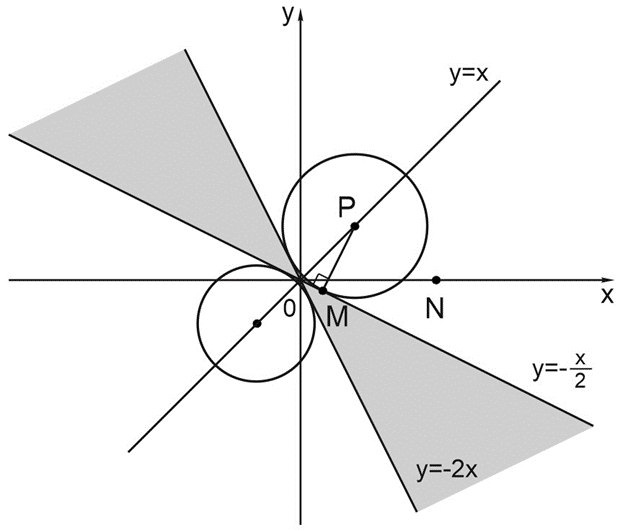
Применим для первого неравенства системы метод областей. Изобразим на координатной плоскости \((x; y)\) прямые, заданные уравнениями \(y+2x=0\) и \(2y+x=0\). Это границы областей. Более привычно записать их в виде \(y=-2x\) и \(y=-\displaystyle \frac{x}{2}\).
Эти прямые разбивают координатную плоскость на области, в каждой из которых выражение \((y+2x)(2y+x)\) в левой части неравенства сохраняет свой знак, то есть либо положительно, либо отрицательно во всей области.
Для проверки знака левой части неравенства возьмем точку \((1;1)\). Для этой точки выражение \((y+2x)(2y+x)\) положительно, и неравенство не выполняется.
При переходе через границу знак левой части неравенства меняется. Области, в которых неравенство выполняется, на рисунке закрашены.
Если \(a=-1\), правая часть второго уравнения равна нулю. В этом случае его решение – точка \((a;a)\), то есть точка \((-1; -1)\), и система не может иметь двух решений.
Если \(a\neq-1\), второе уравнение задает окружность с центром в точке \((a;a)\), то есть на прямой \(y=x\), и радиусом равным \(\displaystyle \frac{|a+1|}{\sqrt{5}}\). Достаточно возвести обе части второго уравнения в квадрат, чтобы убедиться в этом.
Заметим, что окружность с центром на прямой \(y=x\) симметрична относительно этой прямой.
Функции \(y=-2x\) и \(y=-\displaystyle \frac{x}{2}\) являются взаимно обратными, поэтому их графики также симметричны относительно прямой \(y=x\).
И если окружность \(\omega\) касается одной из этих прямых, то касается и второй.
Это значит, что система имеет ровно \(2\) решения, когда заданная вторым уравнением окружность \(\omega\) касается каждой из прямых: \(y=-2x\) и \(y=-\displaystyle \frac{x}{2}\).
Мы помним из геометрии, что окружность касается прямой, когда расстояние от ее центра до этой прямой равно радиусу окружности.
Это значит, что расстояние от точки \(P(a;a)\) до прямой \(y+2x=0\) равно радиусу окружности.
По формуле расстояния от точки \(M(x_0;y_0)\) до прямой \(Ax+By+C=0;\)
\(d=\displaystyle \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}.\)
Получим: \(\displaystyle \frac{|2a+a|}{\sqrt{5}}=\frac{|a+1|}{\sqrt{5}}.\)
\(|3a|=|a+1|;\)
\(9a^2=a^2+2a+1;\)
\(8a^2-2a-1=0;\)
\(a=\displaystyle \frac{1}{2}\) или \(a=-\displaystyle \frac{1}{4}.\)
Значение \(a=\displaystyle \frac{1}{2}\) соответствует случаю, когда окружность находится в I координатной четверти, а значение \(a=-\displaystyle \frac{1}{4}\) – когда она находится в III четверти.
Ответ: \(-\displaystyle \frac{1}{4}\); \(\displaystyle \frac{1}{2}.\)
3. Найдите все положительные значения \(a\), при каждом из которых множеством решений неравенства \(\displaystyle \frac{x-2}{ax^2-(a^2+1)x+a}\geq 0\) является некоторый луч.
Решение:
Разложим на множители знаменатель дроби в левой части неравенства:
\(ax^2-(a^2+1)x+a=(ax-1)(x-a).\)
Неравенство примет вид:
\(\displaystyle \frac{x-2}{(ax-1)(x-a)}\geq 0.\)
Прямые \(x=2\) (сплошная линия), \(a=x\) (штриховая) и кривая \(a=\displaystyle \frac{1}{x}\) (штриховая) разбивают координатную плоскость \((x;a)\) на области, в каждой из который дробь в левой части неравенства сохраняет свой знак.
Для выяснения знаков этого выражения в каждой из областей можно взять, например, точку \(M(3; 1)\).
Для \(x=3\) и \(a=1\) выражение \(\displaystyle \frac{x-2}{(ax-1)(x-a)}\) положительно, значит, в области, в которой лежит точка \(M\), неравенство выполняется.
При переходе через каждую из границ знак левой части неравенства меняется. Согласно условию, мы рассматриваем только положительные \(a\).
На рисунке закрашены области на координатной плоскости \((x; a)\), в которых неравенство выполняется.
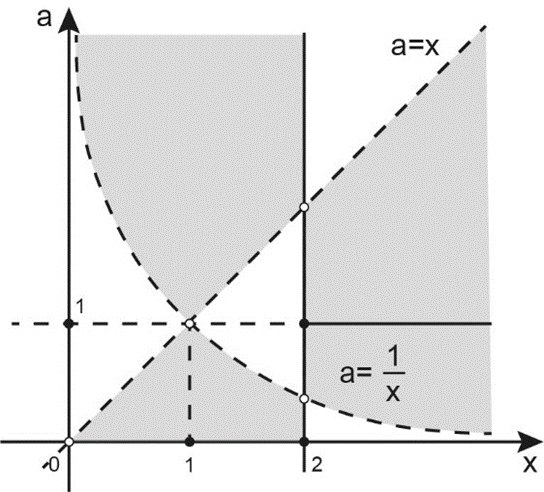
Множество решений данного неравенства при каждом значении \(a\) – это множество абсцисс всех точек этих областей, ордината которых равна \(a\).
Другими словами, для каждого \(a>0\) можно провести горизонтальную прямую. Участки закрашенных областей, лежащие на этой прямой, и будут решениями неравенства.
Например, проведем прямую \(a=2\). В этом случае решениями окажутся два промежутка. Пока что это не луч, как требовалось в условии, так что продолжим наши поиски.
Проведем прямую при \(a=2,5\). И опять не луч, а два промеджутка! И при \(a=0,8\) – тоже два интервала.
А что если провести \(a=1\)? В этом случае решения начинаются с \(x=2\), и множество решений – луч.
Кроме \(a=1\), других таких значений параметра нет.
Ответ: \(a=1\).