Функция — это действие над переменной. Но что будет, если сделать действие — и обратное действие? Открыть дверь и закрыть дверь. Включить свет и выключить свет. Будет то же, что и было раньше, верно? Так и с функциями.
Функции \(f(x)\) и \(g(x)\) называются взаимно-обратными, если \(f(g(x)) = x.\)
Например, \({\left(\sqrt{x}\right)}^2=x\) при \( x \geq 0.\)
Сделали действие (возвели \(x\) в квадрат). Сделали обратное действие (извлекли квадратный корень). И получили то, что и было раньше, то есть переменную \(x\).
А вот \(\sqrt{x^2}=\left|x\right|\). Подумайте, почему это так.
Другой пример взаимно-обратных функций: показательная и логарифмическая. Помните основное логарифмическое тождество: \(\boldsymbol{a^{log_ax}=x}\) для \(x> 0\). Для положительных \(x\) функции \(y = a^x\) и \(y=log_ax\) являются взаимно-обратными.
Еще один пример взаимно-обратных функций:
\(y = sin \;x\) и \(y = arcsin \;x\) при \(x\in \left [-\displaystyle \frac{ \pi }{2};\frac{ \pi }{2}\right] .\)
Вспомним определение функции. Числовая функция \(y = f(x)\) — это такое соответствие между двумя числовыми множествами \(A\) и \(B\), при котором каждому числу \(x\in A\) отвечает одно-единственное число \(y\in B\). Множество \(A\) называется при этом областью определения функции, множество \(B\) — областью значений.
Пусть соответствие \(f\) является взаимно-однозначным:
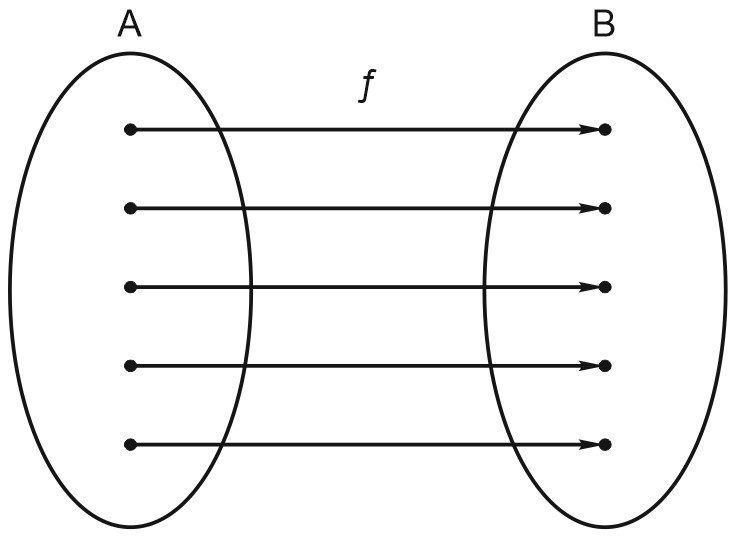
Тогда существует функция \(g\), которая действует в обратную сторону: каждому числу \(y\in B\) она ставит в соответствие одно-единственное число \(x\in A\), такое, что \(f(x) = y\):

Функция \(g\) называется обратной к функции \(f\). Точно так же и функция \(f\) будет обратной к функции \(g\).
Если мы возьмём какое-либо число \(x\in A\) и подействуем на него функцией \(f\), то получим число \(y = f(x)\in B\). Теперь на полученное число \(y\) подействуем функцией \(g\). Куда попадём? Правильно, вернёмся к исходному числу \(x\). Это можно записать так:
| \(g(f(x))=x\) | \((1)\) |
Последовательное применение двух взаимно-обратных действий возвращает нас в исходную точку. Как и в жизни: сначала открыли дверь, а потом совершили обратное действие — закрыли дверь; в итоге вернулись к начальной ситуации.
Так, если возвести число \(3\) в степень \(x\), а затем совершить обратное действие — взять от полученного числа \(3^{x}\) логарифм по основанию \(3\) — мы вернёмся к исходному числу \(x\):
\(log_{3}3^{x}=x.\)
Графики взаимно-обратных функций симметричны относительно прямой \(y=x\).
То, что для функции является областью определения, для обратной функции будет областью значений.
Как вывести формулу обратной функции?
Если вы учитесь в математическом классе или на первом курсе вуза, вам может встретиться такое задание.
Например, у вас есть линейная функция \(y = 2x + 5.\) Какая же функция будет к ней обратной?
Действуем следующим образом:
1) Выражаем из формулы функции \(x\) через \(y\).
Получаем: \(x =\displaystyle \frac{1}{2} (y- 5) = \frac{1}{2} y - \frac{5}{2}.\)
2) В формуле \(x =\displaystyle \frac{1}{2} y - \frac{5}{2}\) меняем \(x\) и \(y\) местами. Получаем формулу обратной функции: \(y =\displaystyle \frac{1}{2} x - \frac{5}{2}\)
Другой пример. Найдем обратную функцию для функции \(y = x^3 + 1\).
1) Выражаем из формулы функции \(x\) через \(y\). Получаем: \(x =\sqrt [3] {y-1}.\)
2) В формуле \(x =\sqrt [3] {y-1}.\) меняем \(x\) и \(y\) местами. Получаем формулу обратной функции: \(y =\sqrt [3] {x-1}. \)

































