Часть 1. Задания с кратким ответом
1. Елена Любецкая В загородном доме живут три семьи: родители с двумя детьми, муж с женой и одинокий пенсионер. Они договорились оплачивать электричество пропорционально количеству потребителей. Первого декабря счетчик электричества показывал 15829 кВт/ч, а 1 января 16 256 кВт/ч, 1 кВт/ч стоит 1 рубль 50 копеек. Сколько заплатит самая большая семья?
2. Сервис «Яндекс» публикует результаты статистических исследований о том, как изменилась жизнь людей в России во время самоизоляции, связанной с коронавирусом. Вот, например, как менялось количество поисковых запросов по ключевым словам «Прокат собак». Показано изменение числа запросов по сравнению с третьей неделей января.
На сколько процентов максимальное число запросов превышает начальное значение?
*Собака в период самоизоляции нужна была для того, чтобы выйти с ней на прогулку и таким образом, иметь возможность отойти на 100 метров от дома.
3. Елена Любецкая Шоколадка имеет прямоугольную форму и состоит из \(m \times n\)
маленьких плиток. Шоколадку можно разломить только по прямой. У Васи есть шоколадка, от которой можно отломить 6 плиток, 4 и 9, и нельзя отломить 5. Сколько плиток в Васиной шоколадке, если их меньше 17?
4. Ольга Чемезова У Дениса в пенале 6 ручек, из которых 3 пишут, а 3 другие – нет. Начинается урок, он случайным образом выбирает ручку из пенала. Найдите вероятность того, что пишущая ручка ему попадётся со второй попытки. При этом считаем, что если ему попадается непишущая ручка, он её откладывает в сторону.
5. Решите уравнение: \(tg \left (\frac{2\pi}{3} \cdot x \right ) = \sqrt{3}\)
В ответе запишите наибольший отрицательный корень.
6. Елена Любецкая В равнобедренном треугольнике АВС на основании АВ взята произвольная точка К. Через К и вершину, противолежащую основанию, провели прямую. Радиус окружности, описанной вокруг треугольника ACK, равен 8. Найдите радиус окружности, описанной вокруг треугольника BCK.
7. Анна Малкова На рисунке изображен график непрерывной функции \(f(x)\) и касательные CD и MN, проведенные к ее графику в точках А и В. Найдите отношение значений производной функции \(f(x)\) в точках А и В.
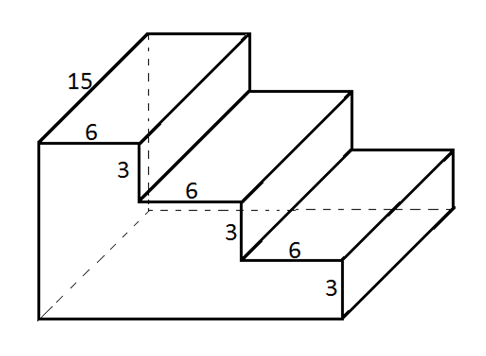
8. Ольга Чемезова
Найдите площадь поверхности «лесенки», изображенной на рисунке. Считайте, что все двугранные углы прямые.
9. Ольга Чемезова
Найдите значение выражения \(log_{0,5}(3-\sqrt{5})+log_{0,5}(3+\sqrt{5})\)
10. Расстояние (в км) от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле \(l=\sqrt{\frac{Rh}{500}}\), где \(R=6400\) км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 6,4 километров?
11. Елена Любецкая У въезда в гетто есть прямоугольная стена шириной 10 метров и длиной 5 метров. Каждый месяц жители покрывают граффити 70% свободного пространства. Когда незакрашенными остаются не более 10% первоначальной площади, стену заново красят. Через сколько месяцев власти города должны будут покрасить стену?
12. Ольга Чемезова Найдите наибольшее значение функции \(y=\frac{1}{x^2+6x+11}.\)
Часть 2. Задания с развернутым ответом
13. Анна Малкова
а) Решите уравнение \(\frac{83sin 2x -168 cos x -83 sin x+84}{2sin x+\sqrt{3}}=0\)
б) найдите все его корни на отрезке \([-\frac{\pi}{2};\frac{9\pi}{2}]\)
14. Анна Малкова
В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD, в котором АВ = 4, BD = \(4\sqrt{2}\) Известно, что SB = \(\sqrt{11}\), SA = SC = \(3\sqrt{3}\).
а) Докажите, что ребро SD перпендикулярно прямой АС.
б) Найдите радиус шара, описанного вокруг пирамиды SABCD.
15. Роман Шашков. Решите неравенство:
\(\left (\sqrt[4]{2} \right )^{x^2+12x+22} \textgreater \sqrt{3+\sqrt{8}}-1\)
16. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая — боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центры окружностей, пересекает основание AD в точке P. Докажите, что \(\frac{AP}{PD}=sin D\).
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.
17. Ольга Чемезова
В марте 2017 года Иван взял кредит в банке. Банк в декабре каждого года начисляет 20% на оставшуюся сумму долга, затем необходимо выплатить часть долга. В марте 2018 года Иван оплатил только начисленные проценты. В марте 2019 года Иван оплатил половину долга, имеющегося на тот момент. В марте 2020 года он погасил долг полностью. Найдите сумму кредита, выданного Ивану, если общая сумма выплат составила 5,32 млн. руб.
18. Елена Любецкая
Найдите значения параметра а, при каждом из которых уравнение имеет натуральные корни:
\(\frac{1-\sqrt{a-4log^2_4x}}{log_{4}x}=2\)
19. (МИОО, 2016) Бесконечная арифметическая прогрессия \(a_1,a_2\dots,a_n\dots\) состоит из различных натуральных чисел. Пусть \(S_1=a_1, S_n=a_1+a_2+\dots+a_n\) при всех натуральных \(n \geq 2.\)
а) Существует ли такая прогрессия, для которой \(S_{10}=100S_1\)?
б) Существует ли такая прогрессия, для которой \(S_{10}=50S_2\)?
в) Какое наименьшее значение может принимать дробь \(\frac{S_5^2}{S_1S_{10}}\)
ВНИМАНИЕ преподавателям и владельцам образовательных сайтов. Мы настоятельно просим вас НЕ ВЫКЛАДЫВАТЬ в интернет условия и тем более решения задач. Мы хотим, чтобы участники имели возможность честно решить задачи.