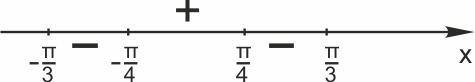Задание 12 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции \(\displaystyle y=-{{x^2+289}\over{x}}.\)
Решение:
Найдем производную функции.
\({y}'=-{\left(\displaystyle\frac{x^{2}+289}{x}\right)}'=-{\left(x+\displaystyle\frac{289}{x}\right)}'=-{\left(1-\displaystyle\frac{289}{x^{2}}\right)}'=\displaystyle\frac{289-x^{2}}{x^{2}}. \)
Приравняем производную к нулю. Получим:
\(x^2=289\Leftrightarrow \left[ \begin{array}{c} \ x=17, \hfill \\ x=-17. \end{array} \right.\)
Исследуем знаки производной.
В точке \(x = 17\) производная \(y'(x)\) меняет знак с «плюса» на «минус».
Значит, \(x= 17\) — точка максимума функции \(y(x).\)
Ответ: 17.
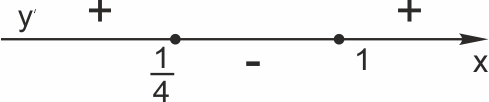
2. Найдите точку минимума функции \(y=2x^2-5x+lnx-3.\)
Решение:
Найдем производную функции.
\(y{'}=4x-5+\displaystyle\frac{1}{x}.\)
Приравняем производную к нулю.
\(4x-5+\displaystyle \frac{1}{x}=0\Leftrightarrow 4x^2-5x+1=0\Leftrightarrow \left[\begin{matrix}x=1, \\x=\displaystyle \frac{1}{4}.\end{matrix}\right.\)
Определим знаки производной.
В точке \(x = 1\) производная \(y'(x)\) меняет знак с «минуса» на «плюс». Значит, \(x= 1\) — точка минимума функции \(y(x).\)
Ответ: 1.
Исследование сложных функций
3. Найдите точку максимума функции \(y=2^{5-8x-x^2}.\)
Решение:
Перед нами сложная функция \(y=2^{5-8x-x^2}.\) Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция \(y=2^t\) монотонно возрастает, точка максимума функции \(y=2^{5-8x-x^2}\) будет при том же \(x_0\), что и точка максимума функции \(t\left(x\right)=5-8x-x^2.\) А ее найти легко.
\(t^{'}\left(x\right)=-8-2x;\)
\(t^{'}\left(x\right)=0\) при \(x=-4\).
В точке \(x = -4\) производная \({{ t}}^{{ '}}\left({ x}\right)\) меняет знак с «плюса» на «минус». Значит, \(x= - 4\) — точка максимума функции \({ t}\left({ x}\right)\).
Заметим, что точку максимума функции \(t\left(x\right)=5-8x-x^2\) можно найти и без производной.
Графиком функции \(t\left(x\right)\) является парабола ветвями вниз, и наибольшее значение \(t\left(x\right)\) достигается в вершине параболы, то есть при \(x=-\displaystyle\frac{8}{2}=-4.\)
Ответ: - 4.
4. Найдите абсциссу точки максимума функции \(y=\sqrt{4-4x-x^2}.\)
Решение:
Напомним, что абсцисса — это координата по \(X\).
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция \(y=\sqrt{z}\) монотонно возрастает, точка максимума функции \(y=\sqrt{4-4x-x^2}\) является и точкой максимума функции \(t\left(x\right)=4-4x-x^2.\)
Это вершина квадратичной параболы \(t\left(x\right)=4-4x-x^2; \; x_0=\displaystyle \frac{-4}{2}=-2.\)
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции \(y=x^3+2x^2-4x+4\) на отрезке \([-2;0].\)
Решение:
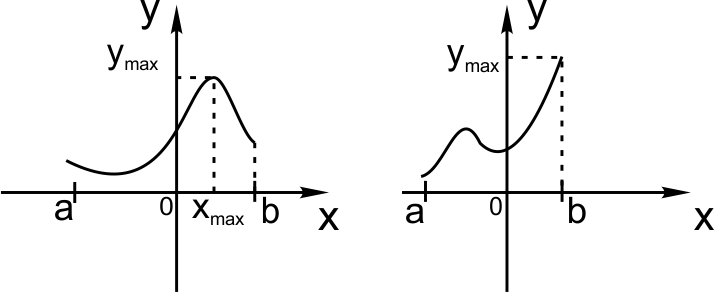
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции \(y=x^3+2x^2-4x+4\) с помощью производной. Найдем производную и приравняем ее к нулю.
\(y'=3x^2+4x-2; \)
\(y'=0; \)
\({3x}^2+4x-4=0; \)
\(D=64; \; x=\displaystyle \frac{-4\pm 8}{6};\)
\(x_1=\displaystyle \frac{2}{3}, \; x_2=-2. \)
Найдем знаки производной.
В точке \(x = - 2\) производная равна нулю и меняет знак с "+" на "-". Значит, \(x = - 2\) — точка максимума функции \(y(x)\).
Поскольку при \(x\in [-2;0]\) функция \(y(x)\) убывает, \(y_{max}\left(x\right)=y\left(-2\right)=12.\)
В этой задаче значение функции на концах отрезка искать не нужно.
Ответ: 12.
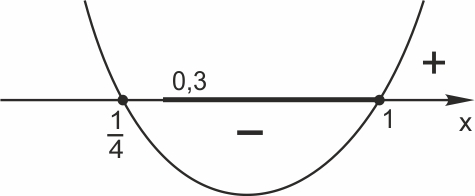
6. Найдите наименьшее значение функции \(y={4x}^2-10x+2lnx-5\) на отрезке \([0,3; 3].\)
Решение:
Найдем производную функции \(y={4x}^2-10x+2lnx-5\) и приравняем ее к нулю.
\(y'\left(x\right)=8x-10+\displaystyle \frac{2}{x}; \; y'(x)=0\) при \(x_1=1, \; x_2=\displaystyle \frac{1}{4}.\)
Найдем знаки производной.
Точка \(x_1=1\) — точка минимума функции \(y\left(x\right)\). Точка \(x_2=\displaystyle \frac{1}{4}\) не лежит на отрезке \([0,3;1].\)
Поэтому \(y(0,3)> y(1)\) и \(y(3)> y(1)\).
Значит, наименьшее значение функции на отрезке \(\left[0,3; 1\right]\) достигается при \(x=1.\) Найдем это значение.
\(y_{min}\left(x\right)=y\left(1\right)=4-10-5=-11. \)
Ответ: -11.
7. Найдите наименьшее значение функции \(y=9x-{\ln \left(9x\right)}+3\) на отрезке \(\left[\displaystyle \frac{1}{18};\frac{5}{18}\right].\)
Решение:
Иногда перед тем, как взять производную, формулу функции полезно упростить.
\( y=9x-{\ln \left(9x\right)}+3=9x-{\ln 9-{\ln x}}+3.\)
Мы применили формулу для логарифма произведения. \( y'\left(x\right)=9-\displaystyle \frac{1}{x}=\frac{9x-1}{x}; \; y'=0\) при \(x=\displaystyle \frac{1}{9}.\)
Если \(0< x< \displaystyle \frac{1}{9}\), то \({y}'(x)< 0.\)
Если \(x> \displaystyle \frac{1}{9}\), то \({y}'> 0.\)
Значит, \( x=\displaystyle \frac{1}{9}\) — точка минимума функции \(y(x)\).
В этой точке и достигается наименьшее значение функции на отрезке \(\left[\displaystyle \frac{1}{18};\frac{5}{18}\right].\)
\(y_{min}\left(x\right)=y\left(\displaystyle \frac{1}{2}\right)=1+3=4. \)
Ответ: 4.
8. Найдите наибольшее значение функции \(y(x)=14x-7tgx-3,5\pi +11\) на отрезке \(\left[-\displaystyle \frac{\pi }{3};\frac{\pi }{3}\right].\)
Решение:
Найдем производную функции \(y(x)=14x-7tgx-3,5\pi +11.\)
\(y'\left(x\right)=14-\displaystyle \frac{7}{{cos}^2x}.\)
Приравняем производную к нулю: \(14-\displaystyle \frac{7}{{cos}^2x}=0.\)
\({cos}^2x=\displaystyle \frac{1}{2}. \)
\({cos}^2x=\pm \displaystyle \frac{1}{\sqrt{2}}=\pm \frac{\sqrt{2}}{2}\).
Поскольку \(x\in \left[-\displaystyle \frac{\pi }{3}; \frac{\pi }{3}\right], \ y'\left(x\right)=0,\) если \(x=\pm \displaystyle \frac{\pi }{4}. \)
Найдем знаки производной на отрезке \(\left[-\displaystyle \frac{\pi }{3};\frac{\pi }{3}\right].\)
\({y}'(0)=14-7> 0;\)
\({y}'\left(\displaystyle \frac{\pi }{3}\right)={y}'\left(-\displaystyle \frac{\pi }{3}\right)=14-28< 0.\)
При \(x=\displaystyle \frac{\pi }{4}\) знак производной меняется с «плюса» на «минус». Значит, \(x=\displaystyle \frac{\pi }{4}\) — точка максимума функции \(y(x).\)
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при \(x=-\displaystyle \frac{\pi }{3}\) и \( x =\displaystyle \frac{\pi }{4}.\)
\(y\left(\displaystyle \frac{\pi }{4}\right)=-7+11=4; \)
\(\left(-\displaystyle \frac{\pi }{3}\right)=-\displaystyle \frac{14\pi }{3}+7tg\displaystyle \frac{\pi }{3}-3,5\pi +11< 4.\)
Мы нашли, что \(y_{max}\left(x\right)=y\left(\displaystyle \frac{\pi }{4}\right)=-7+11=4. \)
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при \(-\displaystyle \frac{\pi }{3}\) не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
Ответ: 4.
9. Найдите наименьшее значение функции \(y=e^{2x}-{8e}^x+9\) на отрезке \([0; 2]\).
Решение:
Снова сложная функция. Запишем полезные формулы:
\({{(e}^{-x})}^{'}=-e^{-x}.\)
\({\left(e^{cx}\right)}^{'}=e^{cx}\cdot c. \)
\({(e}^{x+a})'=e^{x+a}. \)
Найдем производную функции \(y=e^{2x}-{8e}^x+9.\)
\(y'=2e^{2x}-8e^x=2e^x(e^x-4); \)
\(y'=0,\) если \(e^x=4.\) Тогда \(x=ln4.\)
\(0< ln4< 2.\) При \(x=ln4\) знак производной меняется с «минуса» на «плюс».
Значит, \(x=ln4\) — точка минимума функции \(y(x).\)
\(y\left(ln4\right)=4^2-8\cdot 4+9=16-32+9=-7. \)
Ответ: -7.
10. Найдите наибольшее значение функции \(y=12cosx+6\sqrt{3}x-2\sqrt{3}\pi +6\) на отрезке \(\left[0;\displaystyle\frac{\pi }{2}\right].\)
Решение:
Как всегда, возьмем производную функции и приравняем ее к нулю.
\(y'\left(x\right)=-12sinx+6\sqrt{3}; \)
\(y'=0; \) \(12sinx=6\sqrt{3}; \)
\(sinx=\displaystyle\frac{\sqrt{3}}{2}. \)
По условию, \(x\in \left[0;\displaystyle\frac{\pi }{2}\right]\). На этом отрезке условие \(sinx=\displaystyle\frac{\sqrt{3}}{2}\) выполняется только для \(x=\displaystyle\frac{\pi }{3}.\)
Найдем знаки производной слева и справа от точки \(x=\displaystyle\frac{\pi }{3}.\)
\({y}'(0)=6\sqrt{3}> 0;\)
\({y}'\left(\displaystyle \frac{\pi }{2}\right)=-12+6\sqrt{3}< 0.\)
В точке \(x_0=\displaystyle\frac{\pi }{3}\) производная функции меняет знак с «плюса» на «минус». Значит, точка \( x_0=\displaystyle\frac{\pi }{3}\) — точка максимума функции \(y(x)\).
Других точек экстремума на отрезке \(\left[0;\displaystyle\frac{\pi }{2}\right]\) функция не имеет, и наибольшее значение функции \({ y=12cosx+6}\sqrt{{ 3}}{ }{ x}{ -}{ 2}\sqrt{{ 3}}{ }\pi { +6}\) на отрезке \( \left[{ 0};\displaystyle\frac{\pi }{{ 2}}\right]\) достигается при \({ x=}\displaystyle\frac{\pi }{{ 3}}.\)
\(y_{max}\left(x\right)=y\left(\displaystyle\frac{\pi }{3}\right)=12. \)
Ответ: 12.
11. Найдите наименьшее значение функции \(y=16x-6sinx+6\) на отрезке \(\left[0;\displaystyle\frac{\pi }{2}\right].\)
Решение:
Найдем производную функции и приравняем ее к нулю.
\({y}'(x)=16-6cosx; \; 16-6cosx=0; \; cosx=\displaystyle\frac{8}{3}> 1\) — нет решений.
Что это значит? Производная функции \(y=16x-6sinx+6\) не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку \(cosx\le 1\), получим, что \(16-6cosx> 0\) для всех \(x\), и функция \(y\left(x\right)=16x-6sinx+6\) монотонно возрастает при \(x\in \left[0;\displaystyle\frac{\pi }{2}\right].\)
Значит, наименьшее свое значение функция принимает в левом конце отрезка \( \left[{ 0};\displaystyle\frac{\pi }{{ 2}}\right]\), то есть при \(x=0.\)
\(y_{min}\left(x\right)=y\left(0\right)=6. \)
Ответ: 6.