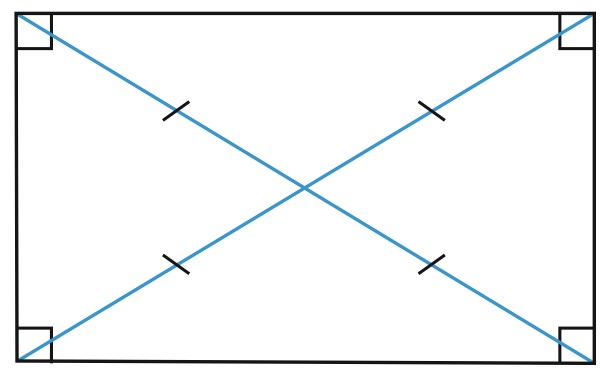
Прямоугольник – это параллелограмм, у которого все углы прямые.
Диагонали прямоугольника равны.
Докажем этот полезный факт.
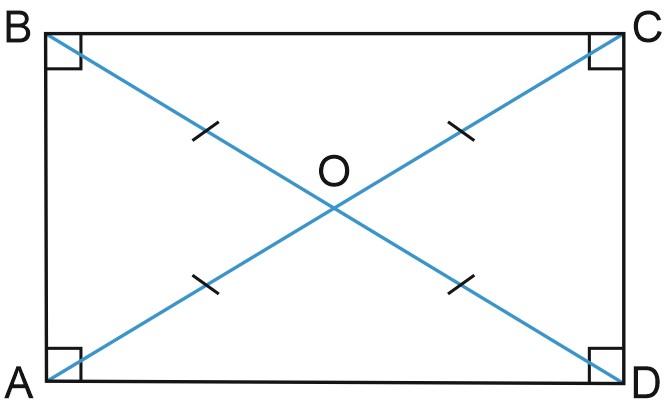
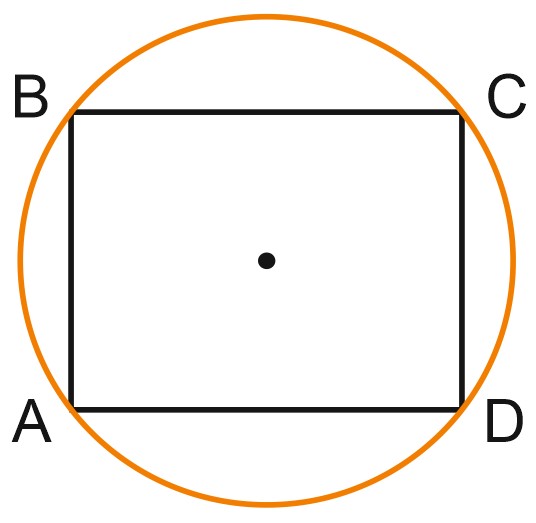
Прямоугольные треугольники \(ABD\) и \(ACD\) равны по углу и двум сторонам. Значит, равные и их гипотенузы, \(AC=BD.\)
1. Меньшая сторона прямоугольника равна \(6\), диагонали пересекаются под углом в \(60^{\circ}\). Найдите диагонали прямоугольника.
Решение:
Диагонали прямоугольника равны, поэтому \(OB=OC, \; OA=OD.\)
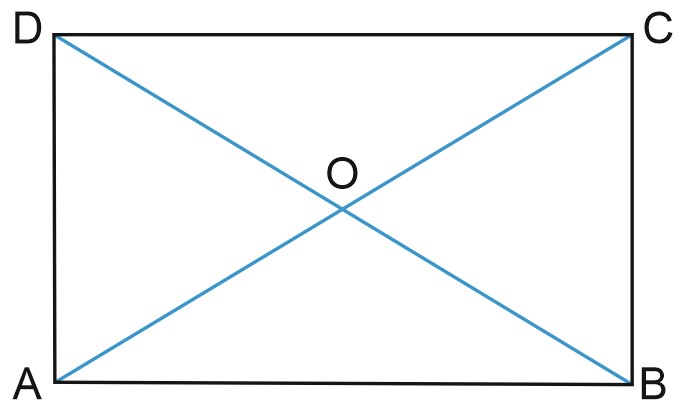
Угол \(COB\) равен \(60^{\circ}\), и треугольник \(OCB\) – равносторонний, \(CB=OC=OB=6.\)
Тогда диагонали \(AC\) и \(BD\) равны \(2OC\), то есть \(12.\)
Ответ: 12.
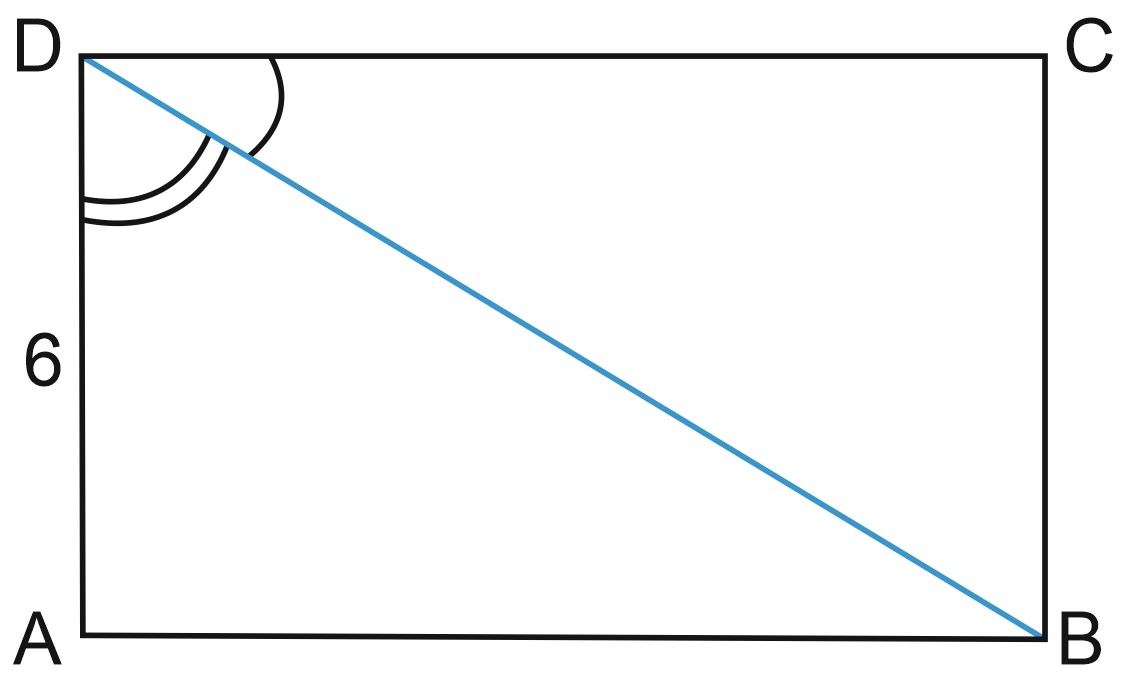
2. В прямоугольнике диагональ делит угол в отношении \(1:2\), меньшая его сторона равна \(6\). Найдите диагональ данного прямоугольника.
Всё просто. Рассмотрите прямоугольный треугольник \(ABD\). Найдите, чему равен угол \(DBA\) и его синус, а затем найдите \(DB\).
Ответ: \(12\).
Рассмотрим еще одну задачу, в которой применяются свойства диагоналей прямоугольника.
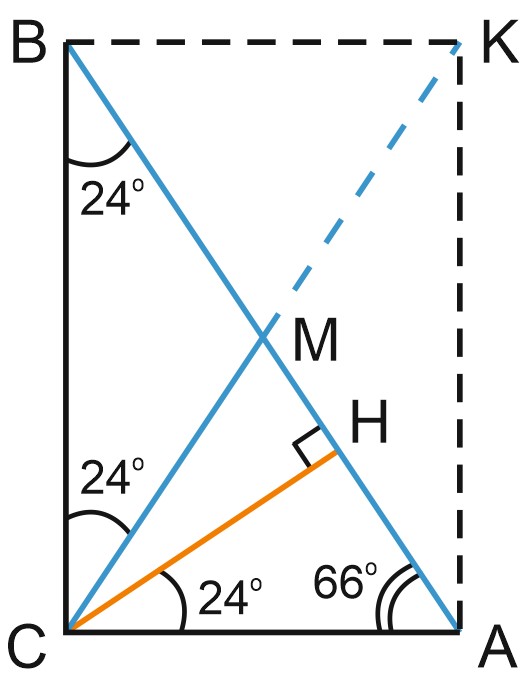
3. Острые углы прямоугольного треугольника равны \(24^{\circ}\) и \(66^{\circ}\). Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Казалось бы, при чем здесь прямоугольник? Дан прямоугольный треугольник, из вершины прямого угла проведены высота и медиана. А что можно сказать о длине этой медианы?
Давайте достроим чертеж до прямоугольника. Поскольку диагонали прямоугольника равны (это свойство прямоугольника) и делятся пополам в точке пересечения, отрезки \(CM, \; BM\) и \(AM\) тоже будут равны. Каждый из них равен половине диагонали прямоугольника. Мы доказали теорему:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Итак, \(BM = CM\), значит, треугольник \(BMC\) равнобедренный, и угол \(BCM\) равен \(24^{\circ}\).
По свойству высоты, проведенной из вершины прямого угла,
\(\angle ACH = \angle ABC = 24^{\circ}\).
Тогда угол \(MCH\) (между медианой и высотой треугольника \(ABC\)) равен \(90^{\circ}-24^{\circ}-24^{\circ}=42^{\circ}.\)
Ответ: \(42\).
Как вы думаете, где находится центр окружности, описанной вокруг прямоугольного треугольника? Ведь центр описанной окружности — точка, равноудаленная от всех вершин треугольника. Очевидно, эта точка — середина гипотенузы.
В прямоугольном треугольнике центром описанной окружности является середина гипотенузы.
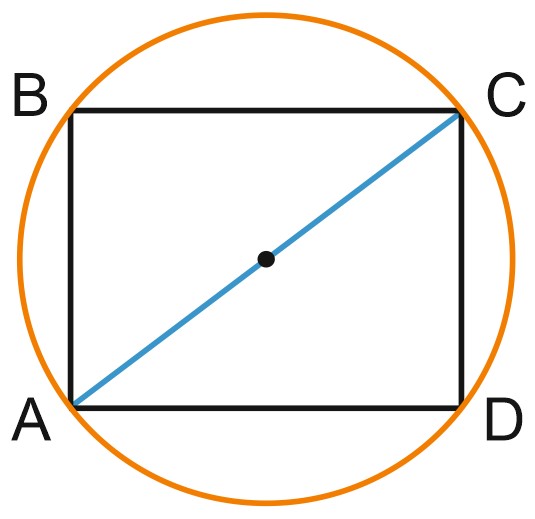
4. Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен \(5\).
Проведем диагональ \(AC\).
Получим, что \(AC\) равна \(2R\).
Ответ: \(10\).