Треугольники. Остроугольный, тупоугольный, прямоугольный.
Равнобедренный и равносторонний треугольники
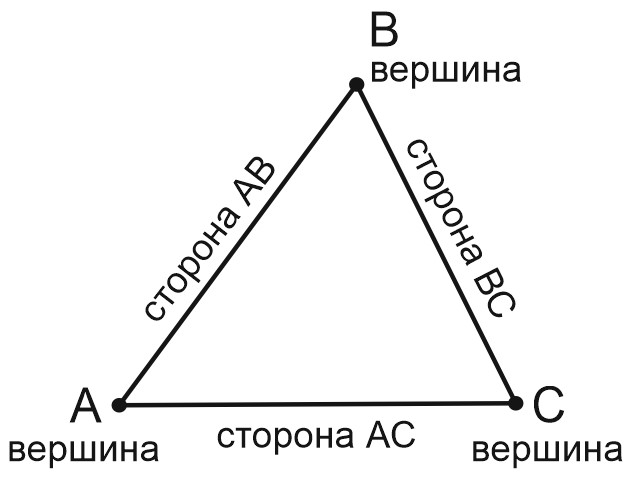
Треугольник – это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.
Углы треугольника принято обозначать тремя буквами: \( \angle ABC, \; \angle BAC, \; \angle BCA\).
Или одной буквой: \(\angle A, \; \angle B, \; \angle C\). Эта буква – вершина угла.
А сам треугольник обозначаем специальным значком: \(\triangle ABC\).
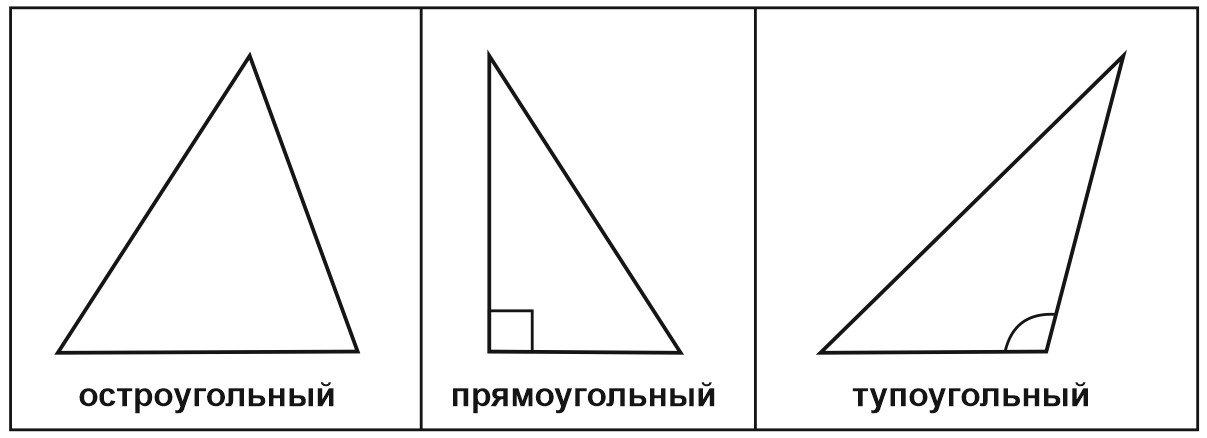
Треугольник, в зависимости от углов, может быть остроугольным, прямоугольным или тупоугольным.
Если в треугольнике есть прямой угол – он прямоугольный.
Если в треугольнике есть тупой угол – он тупоугольный.
Но верно ли утверждение «Если в треугольнике есть острый угол – он остроугольный»?
Подобные вопросы есть в задании ОГЭ, в котором нужно анализировать геометрические выражения и указывать, какие из них верные, а какие – нет.
Посмотрим, сколько острых углов в остроугольном треугольнике? Три.
А в прямоугольном? Два.
А в тупоугольном? Тоже два.
Получается, что в любом треугольнике всегда есть два острых угла.
А если все углы острые – тогда перед нами остроугольный треугольник.
Еще один вопрос на понимание.
Как вы думаете, может ли быть в треугольнике два прямых или тупых угла?
Нет, не может. Сумма углов треугольника равна \(180^{\circ} \). И если мы возьмем два прямых угла, то их сумма будет равна \(180^{\circ} \), и на третий угол просто не останется места.
Если же взять сумму двух тупых углов, то она сразу (даже без третьего угла) будет больше \(180^{\circ} \).
Получается, в любом треугольнике может быть максимум один прямой или тупой угол. А вот острых – может быть 2 или 3.
Равнобедренный и равносторонний треугольники
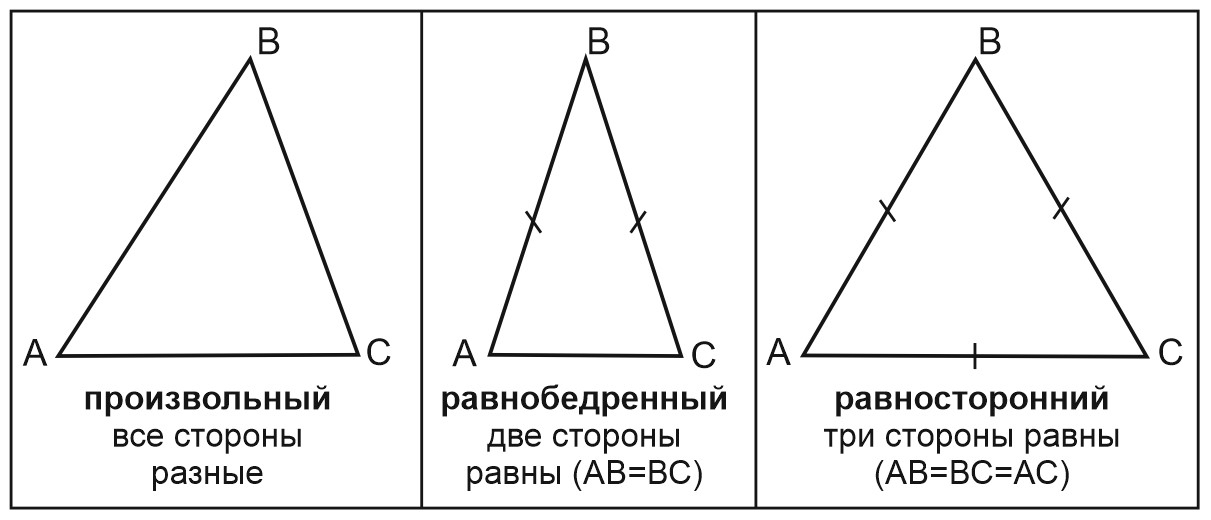
В треугольнике может быть 2 равных стороны, и тогда он называется равнобедренным. А может быть 3 равных стороны, и тогда он называется равносторонним или правильным. Если равных сторон нет, то это произвольный треугольник.
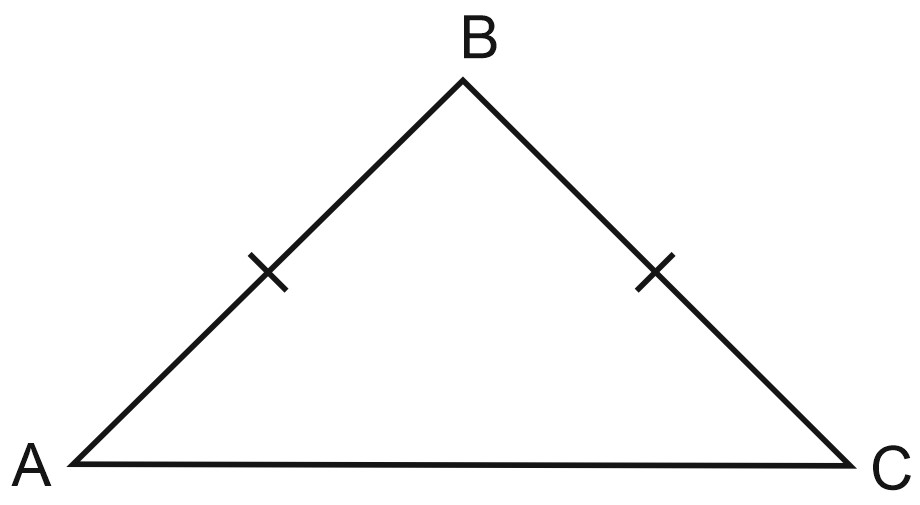
Равнобедренный треугольник – это треугольник, у которого две стороны равны.
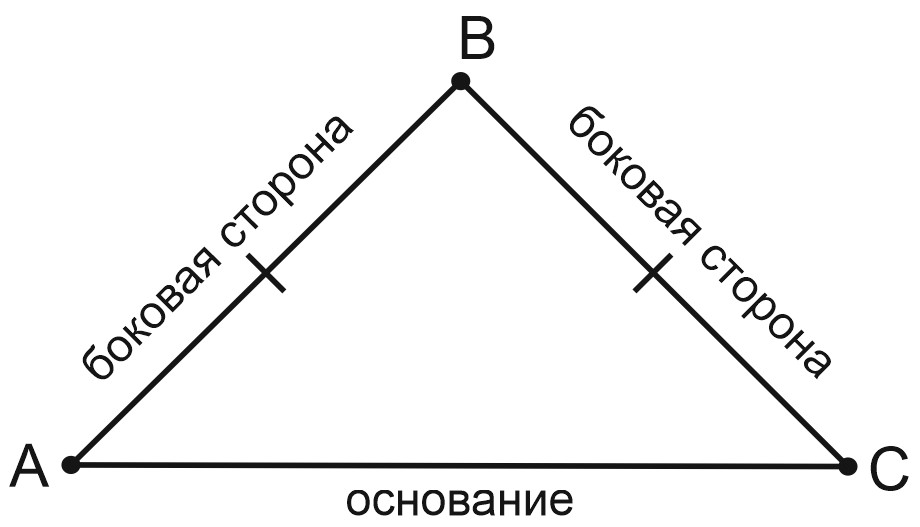
При этом равные стороны называются боковыми сторонами, а третья (не равная им сторона) – основанием.
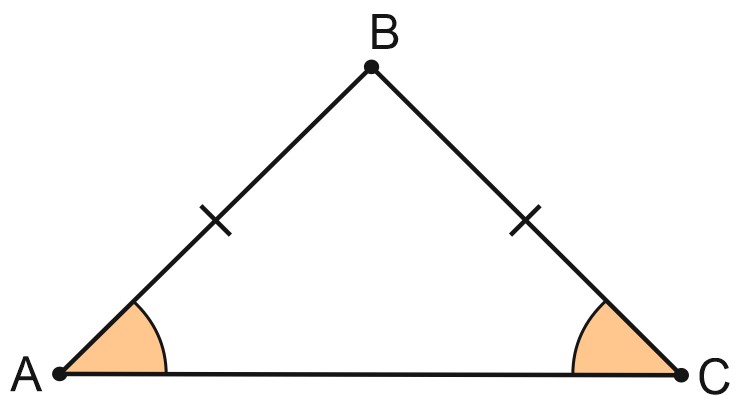
В равнобедренном треугольнике углы при основании равны.
Если по условию дано, что \(AB=BC\), то сразу на чертеже можем обозначить: \(\angle A=\angle C\).
Если в условии сказано, что \(\angle A=\angle C\), то обозначим на чертеже: \(AB=BC\).
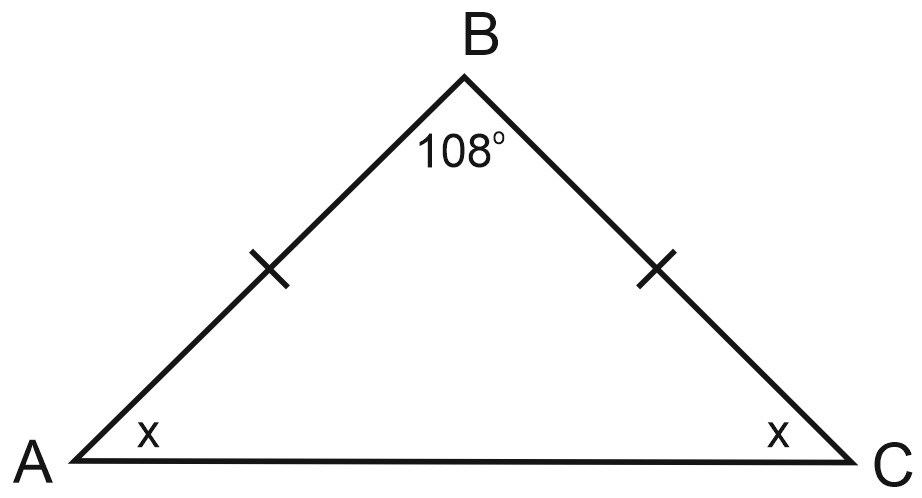
1. В треугольнике \(ABC\) известно, что \(AB=BC, \; \angle ABC=108^{\circ}\). Найдите угол \(BCA\). Ответ дайте в градусах.
Решение:
Отметим на чертеже \(\angle ABC=108^{\circ}\). Две стороны равны, \(AB=BC\), поэтому отметим \(\angle A=\angle C=x\).
Теперь все три угла известны. Составим уравнение, пользуясь тем, что сумма углов треугольника равна \(180^{\circ}\):
\(108^{\circ}+x+x=180^{\circ};\)
\(x=36^{\circ}.\)
Ответ: 36.
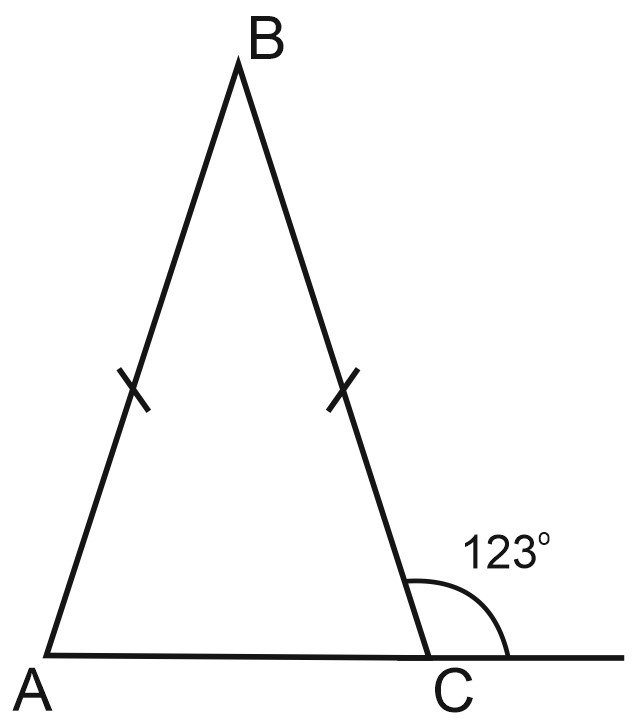
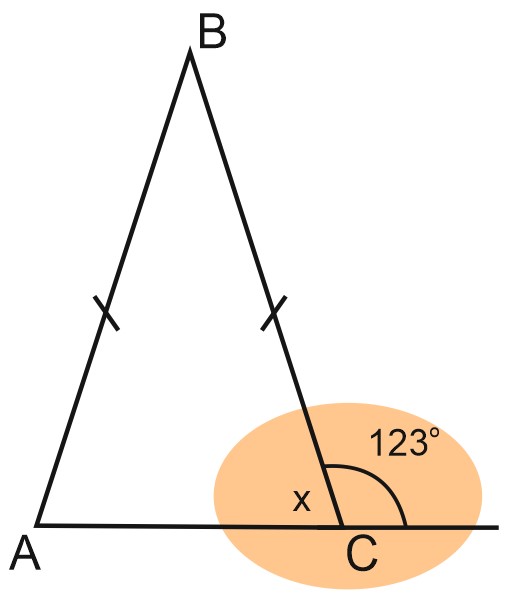
2. В равнобедренном треугольнике \(ABC\) с основанием \(AC\) внешний угол при вершине \(C\) равен \(123^{\circ}\). Найдите величину угла \(ABC\). Ответ дайте в градусах.
Решение:
Рассмотрим угол \(ACB\) и внешний угол \(C\). Это смежные углы, их сумма равна \(180^{\circ}\).
\(x+123^{\circ}=180^{\circ};\)
\(x=57^{\circ}.\)
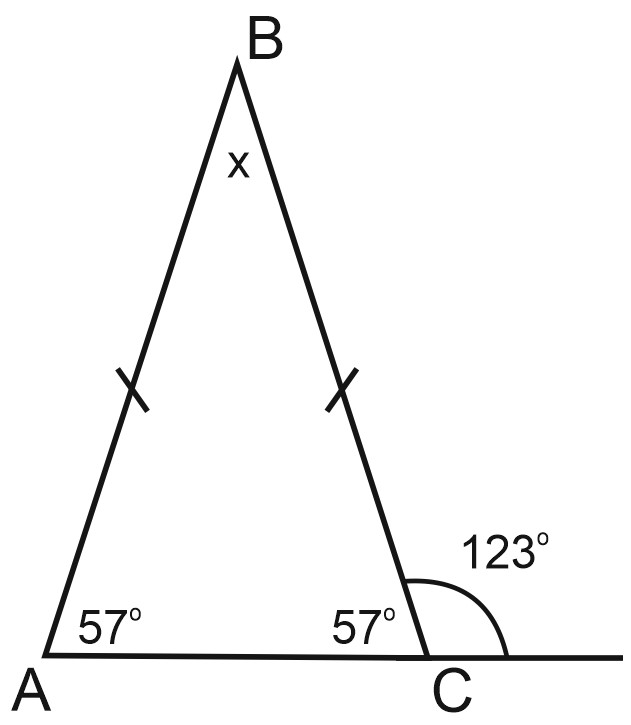
Поскольку треугольник равнобедренный, то \(x=\angle A=\angle C=57^{\circ}\). Отметим на чертеже найденные значения:
Сумма углов треугольника равна \(180^{\circ}\):
\(x+57^{\circ}+57^{\circ}=180^{\circ};\)
\(x=66^{\circ}.\)
Ответ: 66.
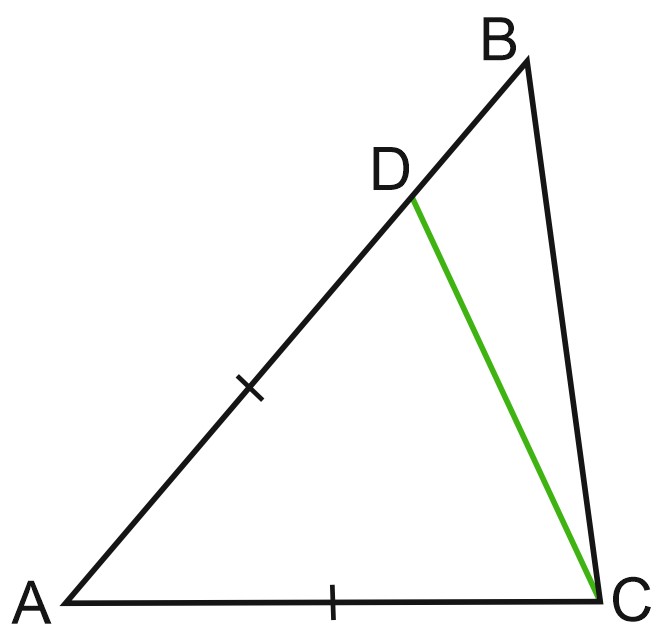
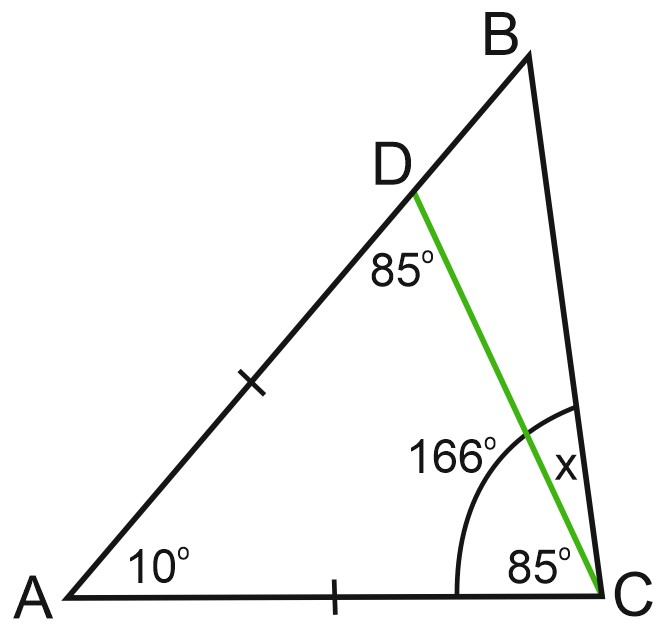
3. Точка \(D\) на стороне \(AB\) треугольника \(ABC\) выбрана так, что \(AD=AC\). Известно, что \(\angle CAB=10^{\circ}\) и \(\angle ACB=166^{\circ}\). Найдите угол \(DCB\). Ответ дайте в градусах.
Решение:
Так как \(AD=AC\), треугольник \(ADC\) – равнобедренный, \(\angle ADC=\angle ACD=x\).
Обозначим на чертеже эти данные и запишем, что сумма углов треугольника \(ADC\) равна \(180^{\circ}\):
\(10^{\circ}+x+x=180^{\circ};\)
\(x=85 ^{\circ}.\)
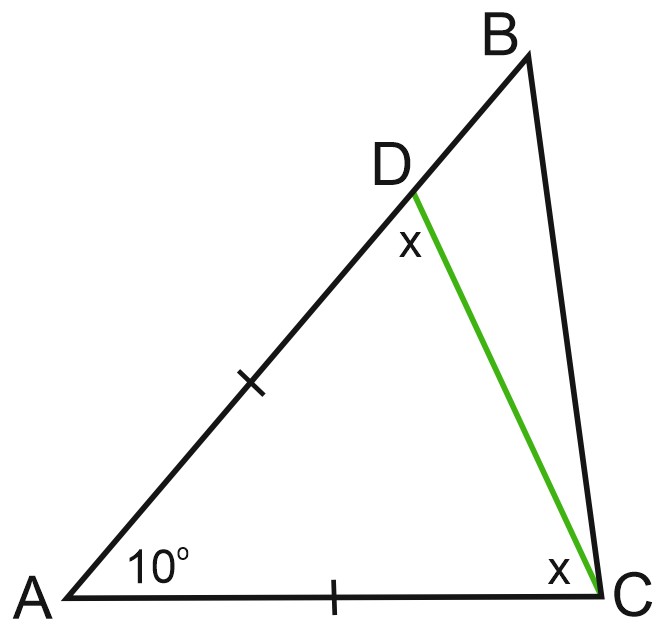
Отметим на чертеже, что мы нашли:
Мы видим, что \(\angle ACB=\angle ACD+\angle DCB\).
Составим уравнение:
\(85^{\circ}+x=166^{\circ};\)
\(x=81 ^{\circ}.\)
Ответ: 81.
Правильный треугольник
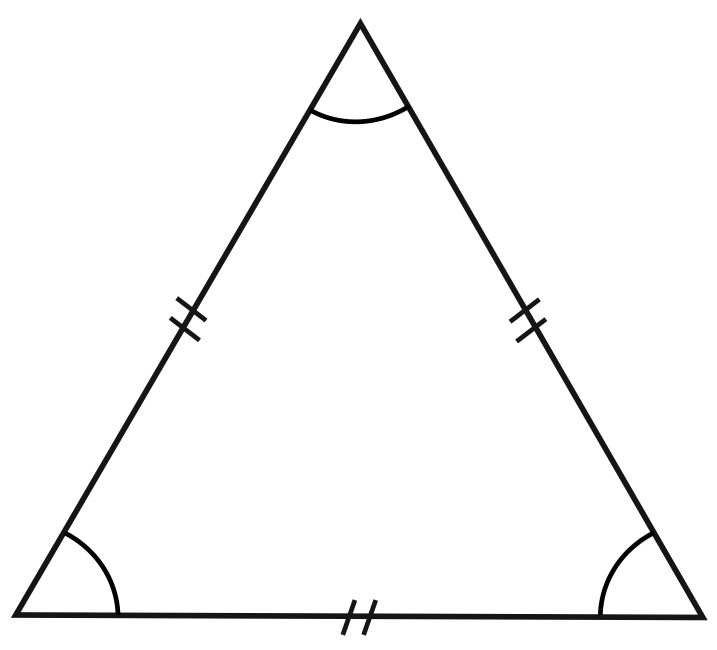
Равносторонний треугольник – это треугольник, у которого все три стороны равны.
Такой треугольник еще называют правильным.
Поскольку равны его стороны, то равны и углы при его вершинах.
Получим уравнение:
\(x+x+x=180^{\circ};\)
\(x=60^{\circ}.\)
Все углы равностороннего треугольника равны \(60\) градусов.
Для равностороннего треугольника выполняются все свойства равнобедренного треугольника. Любая сторона равностороннего треугольника является одновременно и основанием, и боковой стороной.