Видеоразбор варианта 1:
Часть 1. Задания с кратким ответом
1. Анна Малкова На Пробном ЕГЭ по математике Гриша получил некоторое количество баллов. Если бы его результат увеличить на 80%, получилось бы 90 баллов. На сколько баллов Гриша написал Пробный ЕГЭ?
Решение:
Пусть количество баллов, полученное Гришей на Пробном ЕГЭ, равно х.
Увеличив х на 80%, получим \(x + 0,8 x = 1,8 x\),
\(1,8 x = 90\), отсюда х = 50 баллов — первоначальный результат Гриши.
Ответ: 50
2. На графике показано изменение напряжения на конденсаторе в зависимости по времени. Определите, за какое время напряжение на конденсаторе уменьшилось от 1 В до нуля. Ответ выразите в мс.
Решение:
Напряжение на конденсаторе было равно 1 В при \(t_1 = 0,6\) мс и стало равно нулю при \(t_2 = 1,4\) мс. Уменьшение напряжения от 1 В до нуля произошло за 1,4 — 0,6 = 0,8 мс.
Ответ: 0,8
3. Ольга Чемезова
В прямоугольном треугольнике \(ABC\) длина отрезка \(AH = 40\), \(tg A = 0,7\). Найдите \(AB. \)
Решение:
Из \(\vartriangle AHC\), \(CH={90}^{\circ }\):
\( \displaystyle tgA=\frac{CH}{AH}\), отсюда \(CH=40\cdot 0,7=28\)
По свойству высоты прямоугольного треугольника, проведённой к гипотенузе,
\(CH^2=AH\cdot BH; \)
\( \displaystyle BH=\frac{CH^2}{AH}=\frac{{28}^2}{40}=19,6\)
\(AB=AH+BH=40+19,6=59,6 \)
Ответ: 59,6
4. Анна Малкова Маша купила для всей семьи пирожков: 3 с капустой, 3 с вареньем и 4 с рисом. Пирожки лежат в одном пакете и внешне совершенно одинаковы. По дороге домой Маша чувствует непреодолимое желание съесть 2 пирожка, причем разных и не с рисом. С какой вероятностью ей удастся выбрать нужные пирожки из пакета?
Решение: Благоприятными для Маши будут следующие варианты:
1) Первый пирожок, который она вытащит, будет с капустой, а второй с вареньем.
2) Наоборот — первый с вареньем, второй с капустой.
Вероятность достать пирожок с капустой из пакета, в котором всего 10 пирожков, равна 3/10. После того как этот пирожок вытащен, в пакете остается 9 пирожков, из которых 3 с вареньем. Значит, вероятность вытащить пирожок с вареньем равна 3/9 = 1/3, а вероятность достать пирожки с капустой и с вареньем равна 3/10 * 1/3 =1/10, поскольку эти события независимы.
Во втором варианте вероятность достать пирожок с вареньем равна 3/10, а вероятность вытащить после этого пирожок с капустой равна 3/9, произведение этих вероятностей также равно 1/10.
Сложив полученные вероятности, получаем: 0,1 + 0,1 = 0,2.
Ответ: 0,2
5. Решите уравнение \(x^2-6x+\sqrt{6-x}=\ \sqrt{6-x}+7\)
Если уравнение имеет несколько корней, в ответе запишите больший корень.
Решение:
Ответ: -1
6. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Решение:
Сложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.
Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны АС равна 3+ 3 = 6.
Ответ: 22
7. На рисунке изображён график функции \(y=f\left(x\right).\\) Найдите количество точек максимума функции \(y=f\left(x\right)\) на отрезке \([-4; 6]\)
Решение:
По определению, точка максимума — такая внутренняя точка области определения функции, значение в которой больше, чем во всех достаточно близких к ней соседних точках.
Таких точек на графике четыре.
Ответ: 4
8. Площадь основания конуса равна 112. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 2 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Решение:
Плоскость, параллельная основанию, отсекает от конуса меньший конус, все линейные размеры которого в 4 раза меньше, чем у большого. Поэтому площадь сечения в 16 раз меньше площади основания. Она равна 7.
Ответ: 7
9. Найдите значение выражения. \( \displaystyle \sqrt{32}-\sqrt{128}{{sin}^2 \frac{7\pi }{8}\ }.\)
Решение:
\( \displaystyle \sqrt{32}-\sqrt{128}{{sin}^2 \frac{7\pi }{8}\ }=\sqrt{32}-2\sqrt{32}{{sin}^2 \frac{7\pi }{8}=4\sqrt{2}\left(1-{2{sin}^2 \frac{7\pi }{8}\ }\right)=\ } \)
\( \displaystyle =4\sqrt{2}{cos \left(2\cdot \frac{7\pi }{8}\right)=4\sqrt{2}{cos \frac{7\pi }{4}=4\sqrt{2}\cdot \frac{\sqrt{2}}{2}=4.\ }\ } \)
Ответ: 4
10. Анна Малкова
Численность популяции глупых пингвинов описывается уравнением \(P\left(t\right)=P_0\cdot {1,1}^{kt}\), где \(P_0\) — начальная численность популяции, t — время в десятилетиях, прошедшее с момента начала наблюдений. Известно, что через 20 лет после начала наблюдений численность популяции пингвинов увеличилась примерно в 1,331 раза. Найдите k.
Решение:
\(P\left(t\right)=P_0\cdot {1,1}^{kt};\)
t=20 лет=2 десятилетия,
\(P\left(t\right)=1,331P_0={1,1}^3\cdot P_0 \)
Получим:
\({1,1}^3\cdot P_0=P_0\cdot {1,1}^{2k} \)
\(2k=3; \ k=1,5. \)
Ответ: 1,5
11. Анна Малкова
В течение двух месяцев «самоизоляции», вызванной пандемией Covid-19, оборот фирмы предпринимателя Ивана уменьшался на p процентов ежемесячно. Иван подсчитал, что для возвращения к первоначальному уровню оборот необходимо увеличить на 56,25 %. Найдите р.
Решение:
Обозначим X - оборот формы Ивана до "самоизоляции"
\( \displaystyle x\cdot \ {\left(1-\frac{p}{100}\right)}^2\) - оборот фирмы Ивана после двух месяцев "самоизоляции", если величину \(x\cdot \ {\left(1-\frac{p}{100}\right)}^2\) увеличить на 56,25%, то есть умножить на 1,5625, получим x.
\( \displaystyle x\cdot \ {\left(1-\frac{p}{100}\right)}^2\cdot \ \left(1+\frac{56,25}{100}\right)\ =\ x;\)
\( \displaystyle {\left(1-\frac{p}{100}\right)}^2\cdot \frac{156,25}{100}\ =\ 1; \)
\( \displaystyle {\left(1-\frac{p}{100}\right)}^2\ =\frac{100}{156,25} \)
Так как \({12,5}^2\ =\ 156,25,\) получим:
\( \displaystyle {\left(1-\frac{p}{100}\right)}^2\ =\frac{{10}^2}{{\left(12,5\right)}^2}; \)
\( \displaystyle 1-\frac{p}{100}\ =\frac{10}{12,5}\ =\frac{20}{25}\ =\frac{4}{5} \)
\( \displaystyle \frac{p}{100}\ =\ 1\ -\frac{4}{5}\ =\frac{1}{5}; \ \)
\(p=20 \)
Ответ: 20
12. Найдите наибольшее значение функции \( \displaystyle y=\ \frac{1}{x^2-10x+21}\) на отрезке \([4; 6].\)
Решение:
Функция \( \displaystyle y\left(x\right)=\frac{1}{x^2-20x+21}\) определена при всех x, кроме x=3 и x=7 (так как x=3 и x=7 - нули знаменателя); на отрезке [4; 6] функция y(x) непрерывна.
Наибольшее значение функции \( \displaystyle y\ =\frac{1}{x^2-10x+21}\) на отрезке [4; 6] достигается при наименьшем значении знаменателя дроби, т.е. выражения \(t(x)=x^2-10x+21.\)
Так как \(t(x)\) - квадратичная парабола с ветвями вверх, её наименьшее значение достигается в вершине параболы, то есть при \( \displaystyle x_0\ =\frac{10}{2}\ =\ 5; \)
\(4\ \textless \ 5\ \textless \ 6,\) то есть вершина параболы лежит на отрезке [4; 6].
\(t_{min}(x)=t(5)=25-50+21=-4, \)
\(y_{max}(x)=y(-4)=-0,25 \)
Ответ: -0,25
Часть 2. Задания с развернутым ответом
13. Ольга Чемезова
а) Решите уравнение
\( \displaystyle sin2x+2{sin}^2x=2\sqrt{2}sin(x+\frac{\pi }{4}); \)
б) Найдите все его корни на отрезке
\([-2\pi ; \frac{-\pi} {2}] \)
Решение:
а) \( \displaystyle 2{sin x\ }{cos x\ }+2{{sin}^2 x\ }\ =\ 2\sqrt{\left(2\right)}\left({sin x\ }+{cos x\ }\right)\cdot \frac{\sqrt{2}}{2}\)
\({sin x\ }{cos x\ }+{{sin}^2 x\ }\ ={sin x\ }\ +{cos x\ } \)
\({sin x\ }\ \left({sin x\ }\ +{cos x\ }\right)={sin x\ }+{cos x\ } \)
б) \( \displaystyle x\in \left[-2\pi ; -\frac{\pi }{2}\right];\) Отберём корни с помощью тригонометрического круга.
Отметим на тригонометрическом круге отрезок \([\displaystyle -2\pi; -\frac{\pi}{2};]\) и найденные серии решений. Видим, что указанному отрезку принадлежат точки \(\displaystyle -\frac{3\pi}{2};-\frac{5\pi}{4}.\)
б) \( \displaystyle -\frac{3\pi }{2}; -\frac{5\pi }{4}\)
14. Анна Малкова
В основании треугольной пирамиды SABC лежит треугольник АВС, причем его углы А, В и С относятся как 1 : 2 : 3, SO — высота пирамиды.
Известно, что SA = SC = АВ = SB
а) Докажите, что треугольники SCO и ABC равны.
б) Найдите расстояние от точки С до плоскости SAB, если АВ = 8.
Решение:
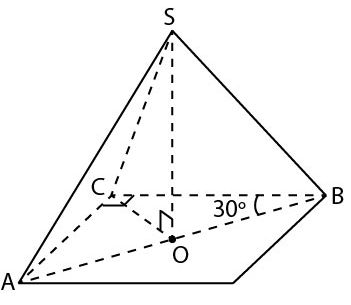
\(\angle A:\angle B:\angle C=1:2:3\Rightarrow \angle A={30}^{\circ },\ \angle B={60}^{\circ },\ \angle C={90}^{\circ }, \)
Если боковые ребра пирамиды равны, ее вершина проецируется в центр описанной окружности основания.
\(SA=SB=SC \Rightarrow O \)— центр описанной окружности \(\vartriangle ABC,\)
O — середина AB, OB=OC=AC.
\(\vartriangle SCO=\vartriangle ABC\) по катету и гипотенузе.
б) Найдём h — расстояние от C до (SAB), если AB=SA=SB=SC=8.
Применим метод объёмов. Рассмотрим треугольную пирамиду SABC:
\( \displaystyle V_{SABC}=\frac{1}{3}S{\vartriangle }_{ABC}\cdot SO=\frac{1}{3} S{\vartriangle }_{SAB}\cdot h \)
\( \displaystyle S_{\vartriangle SAB}=\frac{AB^2\sqrt{3}}{4}=\frac{64\sqrt{3}}{4}=16\sqrt{3} \)
(\(\vartriangle SAB\\) — правильный )
\(8\sqrt{3}\cdot 4\sqrt{3}=16\sqrt{3}\cdot h \)
\(h=2\sqrt{3} \)
Ответ: \(2\sqrt{3}\)
15.
Решить неравенство
\( \displaystyle \sqrt{9x+\frac{1}{2x+1}}\cdot \left(9-25x^2\right)\geq 0. \)
Решение:
\( \displaystyle \sqrt{9x+\frac{1}{2x+1}}\cdot \left(9-25x^2\right)\geq 0\Leftrightarrow
\)
Решим отдельно уравнение:
\(18x^2+9x+1=0 \)
\(D=81-72=9 \)
\( \displaystyle x=\frac{-9\pm 3}{36}; x_1 = - \frac{1}{3}, x_2 = -\frac{1}{6}\)
Получим:
Ответ: \( \displaystyle \left(-\frac{1}{2}; \ -\frac{1}{3}\right]\) или \(\left[-\frac{1}{6}; \frac{3}{5}\right]\)
16. Анна Малкова Биссектрисы \(AA_1,\ BB_1\\) и \(CC_1\) треугольника \(ABC\) продолжены до пересечения с его описанной окружностью, причем \(A_1,\ B_1,\ C_1\) — точки пересечения.
В треугольнике \(A_1B_1C_1\) углы \(A_1,\ B_1\)и \(C_1\) равны 75, 60 и 45 градусов соответственно.
а) Докажите, что \(AB^2\ =\ \ 2\ A_1B_1^2\ \)
б) Пусть О — центр описанной окружности треугольника АВС, Р — точка пересечения его биссектрис. Найдите угол РОВ. Ответ выразите в градусах.
Решение:

\(\angle A={75}^{\circ } \)
\(\angle B_1={60}^{\circ } \)
\(\angle C_1={45}^{\circ } \)
Доказать: \(AB^2=2A_1B^2_1\)
Пусть \(\angle A=2\alpha ,\ \angle B=2\beta ,\ \angle C=2\ \gamma \)
Вписанные углы, которые опираются на равные дуги, равны
\(\left\{ \begin{array}{c}
\angle A_1=\beta +\gamma ={75}^{\circ } \\
\angle B_1=\alpha +\gamma ={60}^{\circ } \\
\angle C_1=\alpha +\beta ={45}^{\circ } \end{array}
\right.\)
Тогда \(\alpha ={15}^{\circ },\ \angle A={30}^{\circ },\)
\(\beta ={30}^{\circ },\ \angle B={60}^{\circ } \)
\(\gamma ={45}^{\circ },\ \angle C={90}^{\circ }, \)
AB — диаметр окружности, \(AB =2R;\)
\(\vartriangle A_1B_1C_1\) —вписан в окружность.
По теореме синусов: \( \displaystyle \frac{A_1B_1}{sin\angle C}=2R; \frac{A_1B_1}{AB}=\frac{\sqrt{2}}{2},\ \)
\(AB^2=2A_1B^2_1. \)
б) \(\vartriangle ABC\) — прямоугольный, \(\angle C={90}^{\circ },\)
\(\angle A={30}^{\circ } \)
P — центр вписанной окружности; O — центр описанной окружности \(\vartriangle ABC.\)
Проведём \(PH\bot AB, PH=r\) (радиус вписанной окружности);
\(PL\bot BC,\ PL=PH \)
Тогда \(BL=BH\) (отрезки касательных, проведенных из одной точки к вписанной окружности, равны). Пусть \(BC=a\), тогда \(AC=a\sqrt{3},\ AB=2a, \)
\(BL=BH=a-r, \)
\(OH=OB-BH=a-\left(a-r\right)=r \)
Рассмотрим \(\vartriangle OPH:\)
\(OH=PH=r,\ \angle H={90}^{\circ }, \)
\(\angle POH=\angle POB={45}^{\circ } \)
Ответ: 45
17. Ольга Чемезова
В начале 2017 года Михаил положил сумму X рублей на депозит в банке. Банк начисляет 10% годовых в конце каждого года на имеющуюся сумму. Начисленные проценты остаются на депозите. В начале 2018 и 2019 годов Михаил пополнял вклад на такую же сумму X, в результате в конце 2019 года сумма на вкладе составила 152922 руб. Найдите сумму X.
Решение:
Составим схему пополнения вклада.
\(k=1,1 \) коэффициент, показывающий, во сколько раз увеличилась сумма вклада после начисления процентов;
К концу 2019 года сумма на депозите Михаила z = 152922 рубля;
\(\left(\left(xk+x\right)\cdot k+x\right)k=z \)
\(x\left(k^3+k^2+k\right)=z \)
\( \displaystyle x=\frac{152922}{{1,1}^3+{1,1}^2+1,1}=\frac{10\cdot 152922}{11\cdot \left({1,1}^2+1,1+1\right)}=\frac{10\cdot 13902}{3,31}=\frac{1000\cdot {1390}^2}{331}=42000 \)
Ответ: 42 000 рублей
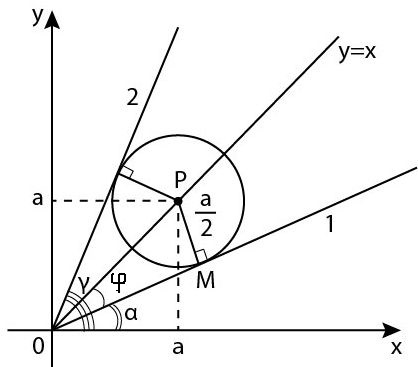
18. Анна Малкова Найдите все значения параметра k, при каждом из которых система уравнений
\( \displaystyle \left\{ \begin{array}{c}
{\left(x-a\right)}^2+{\left(y-a\right)}^2=\frac{a^2}{4} \\
y=kx \end{array}
\right. \)
имеет единственное решение для любого \(a \textgreater 0.\)
Решение:
Решим систему графически в координатах Х, Y.
Первое уравнение задаёт окружность, центр \(\left(a; a\right)\\) радиус \( \displaystyle \frac{a}{2}\)
Система имеет единственное решение, если \(y=kx\) — касательная к окружности.
Центр окружности \(\displaystyle (x-a)^2+(y-a)^2 =\frac{a^2}{4}\) лежит на прямой у = х – биссектрисе угла между положительными направлениями осей Х и Y.
Это значит, что если прямая \(y=kx\) касается окружности \( \displaystyle {\left(x-a_0\right)}^2+{\left(y-a_0\right)}^2=\frac{a^2_0}{4},\) то она будет касаться всех окружностей такого вида для любого a.
Рассмотрим \( \vartriangle OPM:\)
\( \displaystyle\angle M={90}^{\circ },\ PM=r=\frac{a}{2},\ OP=a\sqrt{2} \)
\( \displaystyle {sin \angle \varphi =\frac{PM}{OP}=\frac{1}{2\sqrt{2}}=\frac{1}{\sqrt{8}},\ } \)тогда
\( \displaystyle {cos \angle \varphi =\frac{\sqrt{7}}{\sqrt{8}}\ }; tg\ \varphi =\frac{1}{\sqrt{7}} \)
Для прямой 1:
\(k_1=tg a ; \)
\(a ={45}^{\circ }-\varphi . \)
\( \displaystyle tg a =tg\left({45}^{\circ }-\varphi \right)=\frac{tg{45}^{\circ }-tg\varphi }{1+tg{45}^{\circ }tg\varphi}=\frac{1-tg\varphi }{1+tg\varphi }=\frac{1-\frac{1}{\sqrt{7}}}{1+\frac{1}{\sqrt{7}}}=\frac{\sqrt{7}-1}{\sqrt{7}+1}=
=\frac{{\left(\sqrt{7}-1\right)}^2}{6}=\frac{8-2\sqrt{7}}{6}=\frac{4-\sqrt{7}}{3}. \)
Для прямой 2:
\( \displaystyle k_2tg\gamma =tg\left({45}^{\circ }+\varphi \right)=\frac{tg{45}^{\circ }+tg\varphi }{1-tg{45}^{\circ }tg\varphi }= \)
\( \displaystyle =\frac{1+tg\varphi }{1-tg\varphi }=\frac{\sqrt{7}+1}{\sqrt{7}-1\ }=\frac{{\left(\sqrt{7}+1\right)}^2}{6}=\frac{4+\sqrt{7}}{3} \)
Ответ: \(\frac{4\pm\sqrt{7}}{3} \)
19. На доске написаны 3 натуральных числа. К первому числу приписали справа цифру 6, ко второму — цифру 9, третье оставили без изменений.
а) Могла ли сумма этих чисел увеличиться в 9 раз?
б) Могла ли сумма этих чисел увеличиться в 19 раз?
в) В какое наибольшее целое число раз могла увеличиться сумма этих чисел?
Решение:
Вначале на доске написаны числа: a, b, c, их сумма равна a + b + c.
После того, как к ним приписали цифры, их сумма стала равна
\(10a+6+10b+9+c\)
а) Да, могла.
Предположим, что \(10a+6+10b+9+c=9\left(a+b+c\right)\)
\(a+b+15=8c \)
Пусть \(c=3\), тогда \(a+b=9.\)
Возьмём \(a=2,\ \ b=7.\)
2+7+3=12;
\(26+79+3=108=9\cdot 12. \)
б) Предположим, что
\(10a+6+10b+9+c=19\left(a+b+c\right) \)
\(9a+9b+18c=15 \)
Так как \(a\geq 1,\ b\geq 1,\ c\geq 1,\)
\(9a+9b+18c\geq 36 \textgreater 15\) — противоречие
в) Пусть
\(10a+10b+15+c=m\left(a+b+c\right) \)
\( \displaystyle m=\frac{10a+10b+c+15}{a+b+c}=\frac{10a+10b+10c+15-9c}{a+b+c}=10+\frac{15-9c}{a+b+c} \)
Так как \(a\geq 1,\ b\geq 1,\ c\geq 1,\)
\(a+b+c\geq 3; \)
\( \displaystyle \frac{1}{a+b+c}\leq \frac{1}{3}; \)
\( \displaystyle m\leq 10+\frac{15-9c}{3} \)
Так как \(c\geq 1, -9c\leq -9.\)
\( \displaystyle m\leq 10+\frac{15-9}{3} \)
\(m\leq 12\) (оценка)
Приведём пример для m=12.
Пусть \(a=b=c=1; \)
\(16+19+1=36=12\cdot \left(1+1+1\right). \)
Ответ:
а) да
б) нет
в) 12