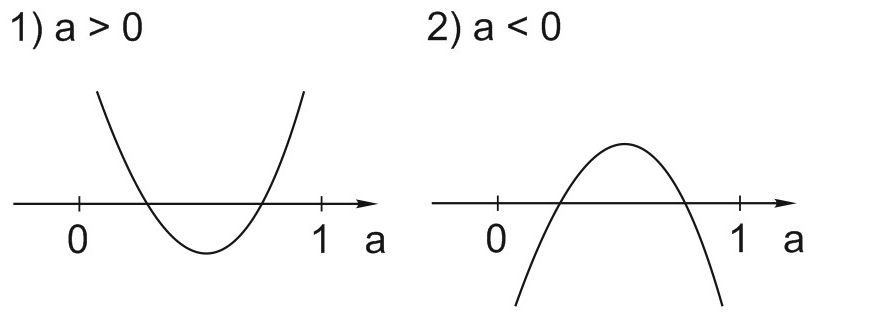Видеоразбор варианта 2:
Часть 1. Задания с кратким ответом
1. Бабушка печет оладушки, причем каждую оладушку необходимо выпекать в течение одной минуты с каждой стороны, а на сковородке помещается не более двух оладушек. Какое наименьшее время (в минутах) нужно бабушке, чтобы испечь 3 оладушки?
Решение:
Кажется, что затраченное время не может быть меньше 4 минут. Но оказывается, что может!
Вначале жарим с одной стороны 2 оладушки. Вторая минута: оладью № 1 переворачиваем, жарим с другой стороны. Оладью №2 откладываем в сторону, вместо нее жарим с одной стороны оладью №3. Третья минута: дожариваем со второй стороны оладьи № 2 и 3.
Ответ: 3
2. На графике показано изменение напряжения на батарейке (в вольтах) в зависимости от времени её использования в фонарике. На оси абсцисс откладываются часы и минуты, на оси ординат – напряжение в вольтах. Известно, что фонарик работает только при напряжении, большем 1,2 В. Сколько минут проработает фонарик на этой батарейке?
Решение: На графике видно, что если время работы батарейки превышает 50 минут, напряжение на ней становится меньше 1,2 В. Значит, фонарик проработает 50 минут.
Ответ: 50.
3. Найдите площадь фигуры, изображенной на клетчатой бумаги с размером клетки 1 x 1 см. Ответ выразите в см².
Решение:
Площадь фигуры получится, если из площади большого квадрата (со стороной 8) вычесть площади четырех фигур:
Прямоугольника размерами 3 х 4 в правом верхнем углу,
Прямоугольного треугольника с катетами 5 и 5, правый нижний угол,
Прямоугольного треугольника с катетами 4 и 6, левый верхний угол,
Прямоугольного треугольника с катетами 2 и 3, левый нижний угол
Получим: \(\displaystyle S = 64 - 12 - \frac{25}{2} - 12 - 3 = 24,5\)
Ответ: 24,5
4. 11 человек случайным образом рассаживаются за круглым столом, среди них Андрей и Наташа. Найти вероятность того, что Андрей и Наташа будут сидеть рядом.
Решим задачу простым способом – без применения формул комбинаторики.
Предположим, что Наташа заняла место за круглым столом. Тогда за столом остается 10 свободных мест. Андрей может занять место слева или справа от Наташи, то есть благоприятных исходов два, а всего 10 исходов, и вероятность того, что Андрей и Наташа окажутся рядом, равна \(\displaystyle \frac{2}{10}\ = 0,2\)
Ответ: 0,2
5. Решите уравнение:
\(\displaystyle \frac{x^2+10}{7x-14}=\frac{x}{x-2\ }\)
Если уравнение имеет несколько корней, в ответе запишите меньший корень.
Решение:
\(\displaystyle \frac{x^2+10}{7\left(x-2\right)}=\frac{x}{\left(x-2\right)}\Leftrightarrow \left\{ \begin{array}{c}
x^2+10=7x \\
x\ne 2 \end{array}
\right.\Leftrightarrow \left\{ \begin{array}{c}
x^2-7x+10=0 \\
x\ne 2 \end{array}
\right.\Leftrightarrow \left\{ \begin{array}{c}
\left(x-2\right)\left(x-5\right)=0 \\
x\ne 2 \end{array}
\right.\Leftrightarrow x=5\)
Ответ: 5
6. Найдите радиус наименьшего круга, в который помещается треугольник со сторонами 6, 7 и 10.
Решение:
В треугольнике со сторонами \(a=6, c=10, b=7\)
\(c^2=a^2+b^2-2ab cos\angle C\) (теорема косинусов)
\(100=36+49-2\cdot 42\cdot cos\angle C,\)
\(\displaystyle {cos \angle C=\frac{36+49-100}{84} \textless 0,\ }\)
\(\angle C\) – тупой, \(\vartriangle ABC\) – тупоугольный.
Прямоугольный треугольник со сторонами 6, 8, 10 можно вписать в круг радиусом 5; Тупоугольный треугольник поместится в круг, в котором диаметр равен его большей стороне, то есть 10. Тогда r=5.
Ответ: 5
7. На рисунке изображен график производной функции f(x), определенной на интервале (-3; 19). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой \(y = 2x + \sqrt{173}\) или совпадает с ней.
Решение:
Если касательная параллельна прямой \(y = 2x\ + \sqrt{173}\) или совпадает с ней, то угловой коэффициент касательной равен 2.
Угловой коэффициент касательной, проведенной к графику функции f(x) в точке с абсциссой \(x_0,\) равен производной функции f(x) в точке \(x_0. \)
Пользуясь графиком производной, изображенным на рисунке, находим количество точек, в которых производная функции равна 2. Таких точек на рисунке 4.
Ответ: 4
8. Высота прямого кругового конуса РО = 7, радиус основания ОА = ОВ = 6, угол АОВ равен \(30{}^\circ.\) Найдите объем треугольной пирамиды РОАВ.
Решение: Объем пирамиды РОАВ: \(\displaystyle V_{POAB}=\frac{1}{3}S_{AOB}\cdot PO\ \)
Площадь треугольника АОВ: \(\displaystyle S_{AOB}=\frac{1}{2}\ OA^2\ \cdot {sin 30{}^\circ \ }=9,\)
\(\displaystyle V_{POAB}=\frac{1}{3}\cdot 9\cdot 7=21\)
Ответ: 21.
9. Ольга Чемезова Вычислите:
\({{log}_{\sqrt{3}} 6\ }-{{log}_{\sqrt{3}} 2\sqrt{3}\ }\)
Решение:
\(\displaystyle {{log}_{\sqrt{3}} 6\ }-{{log}_{\sqrt{3}} 2\sqrt{3}={{log}_{\sqrt{3}} \frac{6}{2\sqrt{3}}={{log}_{\sqrt{3}} \frac{3}{\sqrt{3}}={{log}_{\sqrt{3}} \sqrt{3}\ }=1\ }\ }\ }\)
Ответ: 1
10. Анна Малкова На поверхности планеты Венеры температура Т и атмосферное давление P соответственно равны 750 К и 9120 кПа. Найдите плотность атмосферы у поверхности планеты, считая, что она состоит из углекислого газа с молярной массой М, приближенно равной 44 г/моль, который подчиняется уравнению состояния идеального газа:
\( \displaystyle PV=\frac{m}{M}RT.\)
Здесь m - масса газа, V – его объем. Напоминаем, что плотность – физическая величина, равная отношению массы тела к занимаемому этим телом объему. Универсальную газовую постоянную R приближенно принять равной 8 Дж/(моль * К)
Ответ выразите в кг/м3.
Решение:
Согласно уравнению Клайперона-Менделеева, \(\displaystyle PV=\frac{m}{M}RT\);
Так как плотность \(\displaystyle \rho=\frac{m}{V},\)
\(\displaystyle P=\frac{\rho}{M}RT;\)
11. Найдите скорость поезда, зная, что он проходит мимо неподвижного наблюдателя за 7 секунд и затрачивает 25 секунд на то, чтобы пройти с той же скоростью мимо платформы длиной 378 м. Ответ выразите в км/ч.
Решение:
Пусть скорость поезда равна v.
Так как мимо неподвижного наблюдателя он проезжает за 7 секунд = \(\displaystyle \frac{7}{3600}\) часа, получим:
25 секунд, за которые поезд проезжает мимо платформы, - это время от момента, когда голова поезда поравнялась с началом платформы, до момента, когда хвост поезда поравнялся с концом платформы. За это время поезд проезжает расстояние, равное сумме собственной длины и длины платформы.
Переведем 25 секунд в часы: 25 с = \(\displaystyle \frac{25}{3600}\) часа.
За это время поезд проехал \(\displaystyle S=v\cdot \frac{25}{3600}\)(км)

Приравняем выражения для длины поезда:
\(\displaystyle \frac{7}{3600}\cdot v=\ v\cdot \frac{25}{3600}-0,378\)
\(\displaystyle \frac{18}{3600}\cdot v=0,378\)
\(\displaystyle \frac{1}{200}\cdot v=0,378\)
\(v=0,378\cdot 2=75,6\) км/ч
Ответ: 75,6
12. Найдите наименьшее значение функции \(y = sin x + \sqrt{3} cos x \) на отрезке \(\displaystyle \left[-\frac{\pi}{3}\right.;\left.\frac{5\pi}{3}\right].\)
Решение:
\(\displaystyle y={sin x+\sqrt{3}{cos x=2\cdot \left(\frac{1}{2}{sin x+\frac{\sqrt{3}}{2}{cos x\ }\ }\right)=2\cdot \left({sin x\ }{cos \frac{\pi}{3}+{cos x{sin \frac{\pi}{3}\ }\ }\ }\right)=2{sin \left(x+\frac{\pi}{3}\right)\ }\ }\ }\)
Так как длина отрезка \(\displaystyle \left[-\frac{\pi}{3};\frac{5\pi}{3}\right]\) равна \(2\pi\) (полный круг), наименьшее значение функции \(g\left(t\right)=\sin t\) на этом отрезке равно -1;
Тогда \(y_{min}\left(x\right)=-2.\)
Ответ: -2
Часть 2. Задания с развернутым ответом
13. а) Решите уравнение \(tg8x-tg3x={sin 5x\ }\)
б) Найдите все корни уравнения на отрезке на отрезке \(\displaystyle \left[-\frac{\pi}{2};\ \pi\right]\)
а) \(\displaystyle \frac{{sin 8x\ }}{{cos 8x\ }}-\frac{{sin 3x\ }}{{cos 3x\ }}={sin 5x\ } \)
\(\displaystyle \frac{{sin 8x\ }{cos 3x\ }-{cos 8x\ }{sin 3x\ }}{{sin 8x\ }{cos 3x\ }}={sin 5x\ }\)
\(\displaystyle \frac{{sin 5x\ }}{{cos 8x\ }{cos 3x\ }}-{sin 5x\ }=0\)
\(\left[\ \begin{array}{c}
{sin 5x\ }=0\ \ \ \ \ \ \ \ \ \ \ \ \ \\
{cos 8x\ }{cos 3x\ }=1 \end{array}
\right.\Leftrightarrow \left[ \begin{array}{c}
{\ sin 5x\ }=0\ \ \ \ \ \\
\begin{array}{c}
\left\{ \begin{array}{c}
{cos 8x\ }=1 \\
{cos 3x\ }=1 \end{array}
\right.\ \ \ \\
\left\{ \begin{array}{c}
{cos 8x\ }=-1 \\
{cos 3x\ }=-1 \end{array}
\right. \end{array}
\end{array}
\right.\Leftrightarrow \left[ \begin{array}{c}
\ 5x=\pi n,\ n\in Z\ \ \ (1) \\
\left\{ \begin{array}{c}
8x=2\pi k \\
3x=2 \pi m \end{array}
\ \ \ \ \ \ \ \ \ \ \left(2\right)\right. \\
\left\{ \begin{array}{c}
8x=\pi+2\pi k \\
3x=\pi+2\pi m \end{array}
\ \ (3)\right. \end{array}
\Leftrightarrow \right.\left[ \begin{array}{c}
\ x=\frac{\pi n}{5},\ n\in Z\ \ \ \ \ \ \\
\left\{ \begin{array}{c}
x=\frac{\pi k}{4} \\
x=\frac{2 \pi m}{3} \end{array}
\ \ \ \ \ \ \ \ \ \ \left(2\right)\right. \\
\left\{ \begin{array}{c}
x=\frac{\pi}{8}+\frac{\pi k}{4} \\
\ x=\frac{\pi}{3}+\frac{2 \pi m}{3} \end{array}
\ \ (3)\right. \end{array}
\right.\)
\(n \in Z, m\in Z, k\in Z\)
Мы написали, что произведение \(cos \alpha \cdot cos \beta\) может быть равно 1 только в том случае, если оба множителя по модулю равны 1. Иначе, если один из них по модулю меньше 1, то другой должен быть больше 1, а этого быть не может.
Система (2):
\(\displaystyle x=\frac{\pi k}{4}=\frac{2 \pi m}{3}, k,m \in Z\)
\(\displaystyle 3k=8m,\ k=\frac{8m}{3},\ m\vdots 3,\) тогда \(m=0,\ 3,\ 6,\ 9,\ \dots =3l\)
Значит, \(x=2 \pi l,\ l\in Z\)
Система (3):
\(\displaystyle \frac{ \pi +2\pi k}{8}=\frac{\pi+2 \pi m}{3}\)
\(3\pi+6\pi k=8\pi+16\pi m\)
\(6k=5+16m \), левая часть уравнения всегда четная, правда нечетная – у системы (3) нет решений.
а) Ответ:
\(\displaystyle \left[\ \begin{array}{c}
x=\frac{\pi n}{5} \\
x=2 \pi l \end{array}
\right. \), \(n,l \in Z\)
Заметим, что решения второй серии содержатся среди решений первой. Окончательный ответ: \( \displaystyle x=\frac{\pi n}{5},\ n\in Z\ \)
б) Отберем корни на отрезке \([-\frac{\pi}{2}; \pi ]\) с помощью двойного неравенства.
\(\displaystyle -\frac{\pi}{2}\le \frac{\pi n}{5}\le \pi\)
\(\displaystyle -\frac{1}{2}\le \frac{n}{5}\le 1\)
\(\displaystyle -\frac{5}{2}\le n\le 5\)
\(n=-2;\ -1;\ 0;1;2;3;4;5\)
\(\displaystyle x=-\frac{2\pi}{5};\ -\frac{\pi}{5};\ 0;\ \frac{\pi}{5};\ \frac{2\pi}{5};\ \frac{3\pi}{5};\ \frac{4\pi}{5};\ \pi\)
На данном отрезке уравнение имеет 7 решений.
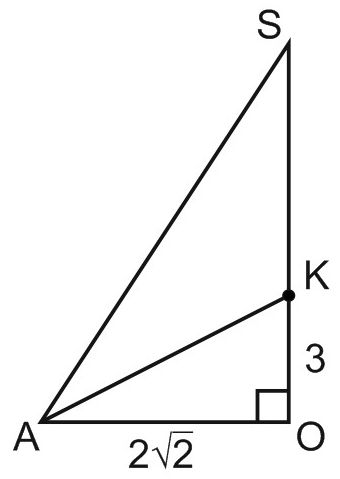
14. Анна Малкова
В прямом круговом конусе с вершиной S отрезок АС – диаметр основания. Точка В лежит на окружности основания конуса, угол АСВ равен \(45{}^\circ. \)
а) Докажите, что SB и АС перпендикулярны.
б) Пусть точка М – середина ВС, АВ = 4, высота конуса равна 9. Найдите угол между прямыми АМ и SB.
Решение:
а) Докажем, что
\(SB \bot AC\)
OB – проекция SB на плоскость ABC,
\(OB \bot AC\), так как треугольник ABC – прямоугольный равнобедренный. Угол В – прямой, поскольку опирается на диаметр, углы А и С равны, следовательно, АВ = АС, отрезок ВО – медиана и высота треугольника АВС.
Тогда
\(SB\bot AC\) по теореме о трех перпендикулярах.
б) Пусть M – середина BC. По условию, AB = 4, SO = 9. Найдем угол между AM и SB.
AM и BO – медианы \(\vartriangle ABC\);
\(AM\cap BO=T;\)
\(\displaystyle BT=\frac{2}{3}BO\), по свойству медиан треугольника.
Проведем \(TK\parallel SB\) в плоскости OSB;
\(\vartriangle OKT\sim \vartriangle OSB,\)
\(\displaystyle OT=\frac{1}{3}BO;\)
\(\displaystyle OK=\frac{1}{3}OS.\)
Рассмотрим \(\vartriangle ATK.\)
По условию, SO=9, тогда OK=3.
\(AC=4\sqrt{2}\) (из \(\vartriangle ABC\));
\(\displaystyle OB=2\sqrt{2}; OT=\frac{2\sqrt{2}}{3}.\)
\(AO=2\sqrt{2}\); из \(\vartriangle AOK\):
\(AK^2=9+8; AK=\sqrt{17}\)
\(\displaystyle TK^2=\sqrt{OT^2+OK^2}=\sqrt{\frac{8}{9}+9}=\frac{\sqrt{89}}{3}\)
Из \(\displaystyle \vartriangle AOT: AT^2=8+\frac{8}{9}=\frac{80}{9}; AT=\frac{4\sqrt{5}}{3}.\)
Рассмотрим \(\vartriangle ATK.\) По теореме косинусов:
\(\displaystyle 17=\frac{89}{9}+\frac{80}{9}-2\cdot \frac{\sqrt{89}}{3}\cdot \frac{4\sqrt{5}}{3}{cos \varphi\ }\)
\(\displaystyle 17=\frac{169}{9}-\frac{8}{9}\cdot \sqrt{89\cdot 5}{cos \varphi\ }\)
\(153=169-8\sqrt{89\cdot 5}{cos \varphi\ }\)
\(\displaystyle {cos \varphi=\frac{16}{8\sqrt{445}}\ }=\frac{2}{\sqrt{445}}=\frac{2\sqrt{445}}{445}\)
15. Анна Малкова
Решите неравенство:
\(\displaystyle \frac{12^2}{5^x-1}-\frac{10^2}{5^x-5}\geq 1\)
Решение:
\(\displaystyle \frac{{12}^2}{5^x-1}-\frac{{10}^2}{5^x-5}\geq 1\)
Замена \(5^x=t, t \textgreater 0\)
\(\displaystyle \frac{144}{t-1}-\frac{100}{t-5}\ge 1\)
\(\displaystyle \frac{144t-144\cdot 5-100t+100}{(t-1)(t-5)}\ge 1\)
\(\displaystyle \frac{44t-620-t^2+6t-5}{(t-1)(t-5)}\ge 0\)
\(\displaystyle \frac{-t^2+50t-625}{\left(t-1\right)\left(t-5\right)}\ge 0\)
\(\displaystyle \frac{t^2-50t+625}{\left(t-1\right)\left(t-5\right)}\le 0\)
\(\displaystyle \frac{{\left(t-25\right)}^2}{\left(t-1\right)\left(t-5\right)}\le 0;\ \ \ \left[ \begin{array}{c}
t=25\ \ \ \ \\
1 \textless t \textless 5 \end{array}
\right.\)
\( \left[ \begin{array}{c}
5^x=25\ \ \ \ \\
1 \textless 5^x \textless 5 \end{array}
\right.\)
Функция \(y=5^x\) монотонно возрастает, и большему значению аргумента соответствует большее значение функции. Получим:
\(\left[ \begin{array}{c}
x=2\ \ \ \ \\
0 \textless x \textless 1 \end{array}
\right.\)
Ответ:
\(x \in (0;2) \cup \left \{ 2 \right \}\)
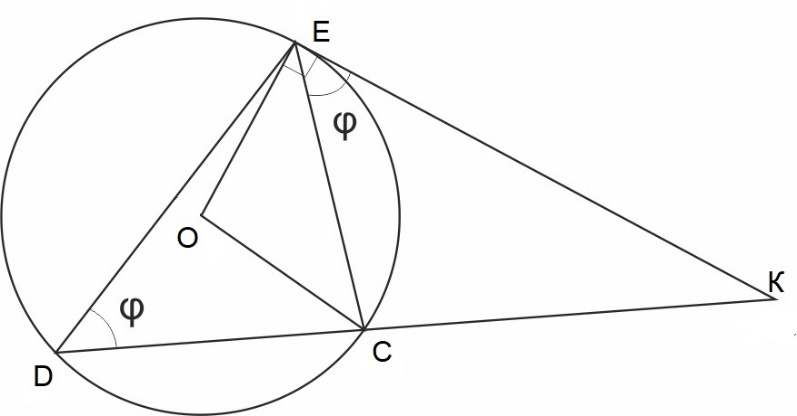
16. В трапеции ABCD с основаниями AD и ВС угол А -- прямой, лучи АВ и DC пересекаются в точке К, точки С и D лежат на окружности, которая касается стороны АВ в точке Е.
a) Докажите, что КЕ : КС = КD : КЕ (другими словами, докажите теорему о секущей и касательной)
б) Известно, что AD =4, ВС = 3, точка F лежит на стороне СD так, что EF перпендикулярна СD.
Найдите EF.
Решение:
а) Докажем, что \(KE^2=KC\cdot KD\)
Докажем сначала, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол ОEK – прямой.
Пусть \(\angle KEC = \varphi.\) Тогда \(\angle OEC=90^\circ - \varphi.\)
Треугольник ОСE – равнобедренный, ОE = ОС (как радиусы окружности). Значит, \(\angle EOC=180^\circ - 2 (90^\circ - \varphi) = 2\varphi.\)
Заметим, что \(\angle EDC = \varphi\) – как вписанный, опирающийся на дугу EC. Значит, углы ЕDС и КЕС равны.
Теорема о касательной и секущей. Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.
Пусть КЕ – касательная, КD – секущая к окружности. Покажем, что \(KE^2=KC \cdot KD.\)
Как мы доказали, \(\angle EDC = \angle KEC = \varphi \) и это значит, что треугольники KEC и KDE подобны по двум углам. Запишем соотношение сходственных сторон:
\(\displaystyle \frac{KE}{KD}=\frac{KC}{KE}.\) Отсюда \(KE^2 = KC \cdot KD.\)
б) AD = 4, BC = 3
\(EF\bot CD; EF - ?\)
\(\triangle KBC\sim \triangle KAD\) по двум углам, отсюда \(\displaystyle AB=\frac{1}{4}AK=\frac{1}{3}BK\)
Пусть \(\angle ADC=\angle BCK=\alpha\)
\(\displaystyle KC=\frac{3}{{cos \alpha }}, CD=\frac{1}{{cos \alpha }}, KD=\frac{4}{{cos \alpha }};\)
Проведем \(\displaystyle AH\bot KD, AH=\frac{4}{{sin \alpha\ }}.\)
Из пункта (а): \(\displaystyle KE^2=KC\cdot KD, KE^2=\frac{12}{{{cos}^2 \alpha}}, KE=\frac{2\sqrt{3}}{{cos \alpha }};\)
\(\triangle AHK\sim \triangle EFK;\)
\(AK=KD\cdot {sin \alpha }\)
\(\displaystyle \frac{AH}{EF}=\frac{AK}{EK};\)
\(\displaystyle EF=\frac{AH\cdot EK}{AK}=\frac{4\cdot {sin \alpha }\cdot 2\sqrt{3}\cdot {cos \alpha }}{{cos \alpha }\cdot {sin \alpha }\cdot 4}=2\sqrt{3}. \)
Ответ: \( 2 \sqrt{3}\)
17. Анна Малкова
По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 5% сумму, имеющуюся на вкладе, а по вкладу «Б» увеличивает эту сумму на 8 % в течение каждого из первых двух лет. Какое наименьшее целое неотрицательное число процентов может начислить банк по вкладу «Б» за третий год, чтобы вклад «Б» оказался выгоднее вклада «А»?
Решение:
Пусть первоначальная сумма вклада равна S. По вкладу А начисляется 5% годовых. Это значит, что за три года хранения сумма вклада увеличится в \(1,05^2\) раза. По вкладу Б начисляется 8% годовых. За два года сумма вклада увеличится в \(1,08^2\) раза.
Пусть за третий год начислено р процентов по вкладу Б. Тогда за третий год сумма на вкладе Б увеличится в \(\displaystyle k = 1+\frac{p}{100}\) раза. Чтобы вклад Б оказался выгоднее вклада А, необходимо, чтобы выполнялось строгое неравенство:
\( 1,08^2 kS \textgreater 1,05^3 S. \)
Это значит, что
\(1,08^2 k \textgreater 1,05^3 . \)
\(\displaystyle \frac{{108}^2}{{100}^2}k \textgreater \ \frac{{105}^3}{{100}^3}\)
\(\displaystyle {108}^2k \textgreater \ \frac{{105}^3}{{100}^{\ }}\)
Разделим обе части неравенства на 9.
\(\displaystyle {36}^2k \textgreater \ \frac{{105\cdot 35}^2}{{100}^{\ }}\)
\(\displaystyle k \textgreater \ \frac{{35\cdot 7}^2}{4^{\ }\cdot 36\cdot 12}\)
\(\displaystyle k \textgreater \ \frac{{35\cdot 49\ \ \ }^{\ }}{36\cdot {48}^{\ }}\)
\(\displaystyle k \textgreater \ \frac{{35\cdot 49\ \ \ }^{\ }}{36\cdot {48}^{\ }}\)
Запишем неравенство в виде:
\(\displaystyle k \textgreater \ \frac{{(36-1)\cdot (48+1)\ \ \ }^{\ }}{36\cdot {48}^{\ }}\)
\(\displaystyle k \textgreater \left(1-\frac{1}{36}\right)\left(1+\frac{1}{48}\right)\)
(мы стараемся решить задачу без калькулятора, поэтому упрощаем вычисления)
\(\displaystyle k \textgreater 1-\ \frac{1}{36}+\frac{1}{48}-\frac{1}{36\cdot {48}^{\ }}\)
\(\displaystyle k \textgreater 1-\ \frac{1}{144}-\frac{1}{36\cdot {48}^{\ }}\)
\(\displaystyle k \textgreater 1-\ \frac{1}{144}-\frac{1}{36\cdot {48}^{\ }}\)
\(\displaystyle k \textgreater 1-(\frac{1}{144}+\frac{1}{36\cdot {48}^{\ }})\)
\(\displaystyle k \textgreater 1-\frac{13}{36\cdot {48}^{\ }}\)
Заметим, что k =1 – решение неравенства. Это значит, что по вкладу Б банк может вообще не начислять процентов в третий год. Целый неотрицательный ответ: 0.
Ответ: 0
18. Найдите все значения параметра а, при которых уравнение
\(\displaystyle \left(a+1\right){tg}^2x-\frac{2a+4}{{cos x\ }}-7a+1=0\)
имеет более одного решения на интервале \(\displaystyle \left(0;\frac{\pi}{2}\right).\)
Решение:
Применим формулу
\(\displaystyle 1+{tg}^2x=\frac{1}{{{cos}^2 x\ }} ;\) отсюда
\(\displaystyle tg^2x=\frac{1}{{{cos}^2 x\ }}-1\) Получим:
\(\displaystyle \left(\frac{1}{{{cos}^2 x\ }}-1\right)\left(a+1\right)-\frac{2a+4}{{cos x\ }}-7a+1=0\)
ОДЗ:
\({cos x\ }\ne 0\)
Домножим обе части уравнения на \(cos^2 x \ne 0 \)
\(\left(1-{{cos}^2 x\ }\right)\left(a+1\right)-\left(2a+4\right){cos x\ }-\left(7a-1\right){{cos}^2 x\ }=0\)
Замена \({cos x\ }=t.\)
Так как, по условию, \(\displaystyle 0 \textless x \textless \frac{\pi}{2}, 0 \textless t \textless 1.\)
Функция \(y=cos x\) монотонно убывает при \(0 \textless x \textless \frac{\pi}{2},\) поэтому на этом интервале каждому t соответствует единственное значение х.
Получим:
\(\left(a+1\right)\left(1-t^2\right)-\left(2a+4\right)t-\left(7a-1\right)t^2=0\)
\(8at^2+\left(2a+4\right)t-\left(a+1\right)=0\)
При \(a = 0\) это линейное уравнение, и оно имеет не более одного решения – не подходит по условию задачи.
При \(a \ne 0\) это квадратное уравнение, и оно может иметь не более двух решений.
Найдем, при каких a уравнение имеет два решения на интервале \(\left(0;1\right).\)
Для этого необходимо, чтобы дискриминант квадратного уравнения был положителен, а вершина \(t_0\) лежала на интервале (0; 1).
Если \(a \textgreater 0,\) то значения квадратичной функции \(y=8at^2+(2a+4)t-(a+1)\) в точках 0 и 1 должны быть положительны.
Если \(a \textless 0,\) то значения квадратичной функции \(y=8at^2+(2a+4)t-(a+1)\) в точках 0 и 1 должны быть отрицательны.
\(
\left\{\begin{matrix}
f(0)\textgreater0\\ f(1)\textgreater0
\\ 0\textless t_0\textless 1
\\ D\textgreater0
\\ a\textgreater0
\end{matrix}\right.\) или \(
\left\{\begin{matrix}
f(0)\textless0\\ f(1)\textless0
\\ 0\textless t_0\textless 1
\\ D\textgreater0
\\ a\textless0
\end{matrix}\right.\)
Запишем условия \(D \textgreater 0\) и \(0 \textless t_0 \textless 1\)
\(\left\{ \begin{array}{c}
{\left(2a+4\right)}^2+32a\left(a+1\right) \textgreater 0 \\
0 \textless -\frac{2a-4}{16a} \textless 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{array}
\right.\)
\(\displaystyle \left\{ \begin{array}{c}
{\left(3a+2\right)}^2 \textgreater 0 \\
0 \textless -\frac{a+2}{8a} \textless 1 \end{array}
\right. a\ne -\frac{2}{3}\)
\(\displaystyle \left\{ \begin{array}{c}
a\ne -\frac{2}{3} \\
\frac{a+2}{a} \textless 0 \\
\frac{9a+2}{a} \textgreater 0 \end{array}
\right.\)
Получим, что \(a\in \left(-2;\ -\frac{2}{3}\right)\cup \left(-\frac{2}{3};\ -\frac{2}{9}\right)\)
Рассмотрим остальные условия:
\(\left[ \begin{array}{c}
\left\{ \begin{array}{c}
a \textgreater 0 \\
f\left(0\right) \textgreater 0 \\
f\left(1\right) \textgreater 0 \end{array}
\right. \\
\left\{ \begin{array}{c}
a \textless 0 \\
f\left(0\right) \textless 0 \\
f\left(1\right) \textless 0 \end{array}
\right. \end{array}
\right. ; \left[ \begin{array}{c}
\left\{ \begin{array}{c}
a \textgreater 0 \\
-a-1 \textgreater 0 \\
8a+2a+4-a-1 \textgreater 0 \end{array}
\right. \\
\left\{ \begin{array}{c}
a \textless 0 \\
-a-1 \textless 0 \\
9a+3 \textless 0 \end{array}
\right. \end{array}
\right.\ \)
\(\left[ \begin{array}{c}
\left\{ \begin{array}{c}
a \textgreater 0 \\
a \textless -1 \\
a \textgreater -\frac{1}{3} \end{array}
\right. \\
\left\{ \begin{array}{c}
a \textless 0 \\
a \textgreater -1 \\
a \textless -\frac{1}{3} \end{array}
\right. \end{array}
\right.\)
Значит, \(-1 \textless a \textless -\frac{1}{3}\)
Получим:
\(\left\{ \begin{array}{c}
-1 \textless a \textless -\frac{1}{3} \\
\left[ \begin{array}{c}
-2 \textless a \textless -\frac{2}{3} \\
-\frac{2}{3} \textless a \textless -\frac{2}{9} \end{array}
\right. \end{array}
\right.\)

Ответ: \(\displaystyle a\in \left(-1;-\frac{2}{3}\right)\cup \left(-\frac{2}{3};-\frac{1}{3}\right).\)
19. Рассматриваются конечные непостоянные арифметические прогрессии, состоящие из натуральных чисел, которые не имеют простых делителей, отличных от 2 и 3.
а) Может ли в этой прогрессии быть три числа?
б) Какое наибольшее количество членов может быть в этой прогрессии?
Решение.
а) В такой прогрессии может быть три члена: например, 2, 4, 6.
6) В такой прогрессии может быть четыре члена: например, 1, 2, 3, 4.
Предположим, что существует такая арифметическая прогрессия, состоящая не менее чем из пяти членов. Рассмотрим любые пять её последовательных членов. Разделим каждый член на наибольший общий делитель всех пяти членов. Поскольку разности соседних членов уменьшатся в одинаковое число раз, полученные числа \(a_1,\ a_2,\ a_3,\ a_4,\ a_5\) также образуют арифметическую прогрессию, удовлетворяющую условию задачи. Заметим, что числа \(a_1,\ a_2,\ a_3,\ a_4,\ a_5\) не могут все быть четными или все делиться на 3.
Если разность этой прогрессии делится на 3, то в ней не может быть члена, делящегося на 3 (иначе все члены прогрессии делятся на 3), поэтому все члены прогрессии являются степенями двойки. Поскольку все члены не могут быть четными, получаем, что среди них присутствует 1. Но в этом случае разность прогрессии нечетна, поэтому чётные и нечетные члены прогрессии чередуются, а нечётных степеней двойки, отличных от 1, не существует.
Пусть теперь разность прогрессии d не делится на 3. Тогда если a_1 делится на 3, то члены \(a_2=a_1+d, a_3=a_1+2d\) и \(a_5+a_1+4d\) не делятся на 3, а \(a_4=a_1+3d\) делится на 3. Аналогично, если \(a_2\) делится на 3, то из чисел \(a_1,\ a_2,\ a_4,\ a_5\) на 3 будет делиться только \(a_5.\) Наконец, если \(a_3\) делится на 3, то ни одно из чисел \(a_1,\ a_2,\ a_4,\ a_5\) не делится на 3. Значит, найдутся два последовательных члена прогрессии, являющиеся степенями двойки.
Если оба эти члена четны, то и все члены прогрессии чётны, чего не может быть. Поэтому одно из этих чисел -- единица. Единица может стоять в прогрессии только на первом или пятом месте, в этом случае на 3 делится только a_3, поскольку единица --- один из двух последовательных членов прогрессии, являющихся степенями двойки. Тогда \(a_1,\ a_2,\ a_4,\ a_5\) являются степенями двойки. Разность прогрессии \(d=a_2-a_1=a_5-a_4,\) значит, она чётна и все члены прогрессии чётны, чего не может быть.
Ответ: а) да; б) 4.