Вариант 4, решения

Видеоразбор варианта 4:

Часть 1. Задания с кратким ответом

1. Автомобиль увеличил скорость на 150%. На сколько процентов меньше времени ему потребуется теперь для прохождения того же расстояния?

Решение.

Составим таблицу

1)	$v$	$t$	$S$
2)	$v_1$	$t_1$	$S$

$v_1=v+150%V=2,5v;$

$v_1t_1=v\cdot t$

$2,5v\cdot t_1=v\cdot t$

$\displaystyle t_1=\frac{t}{2,5}=\frac{4t}{10}=\frac{40t}{10}=0,4t,$

Время уменьшилось на 60%

Ответ: 60

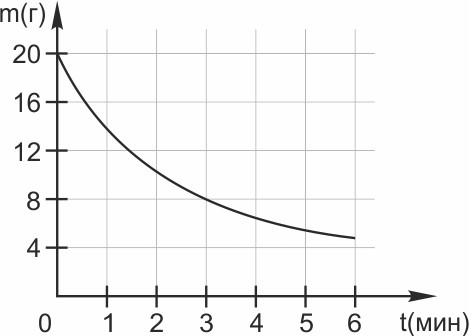
2. В ходе химической реакции количество исходного вещества (реагента), которое еще не вступило в реакцию, со временем постепенно уменьшается. На рисунке эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат – масса оставшегося реагента, который еще не вступил в реакцию (в граммах). Определите по графику, сколько граммов реагента вступило в реакцию за три минуты?

Решение:

Это задача на внимательность. На графике показано изменение массы оставшегося реагента, а найти количество вещества, вступившего в реакцию. Согласно графику, в начальный момент времени было 20 граммов реагента, а через три минуты стало 8 граммов. Следовательно, в реакцию вступило 12 граммов вещества.

Ответ: 12.

3. Анна Малкова Найдите площадь прямоугольного треугольника, если его гипотенуза равна 6, а острый угол равен $15{}^\circ.$

$\displaystyle S_{\triangle ABC}=\frac{a\cdot b}{2};$

$\displaystyle {sin A=\frac{a}{c}\Rightarrow a=c\cdot {sin {15}^{\circ },\ }\ }$

$\displaystyle {cos A=\frac{b}{c}\Rightarrow b=c\cdot cos {15}^{\circ },\ }$

$\displaystyle S_{\triangle ABC}=\frac{1}{2}c^2\cdot {sin {15}^{\circ }{cos {15}^{\circ }=\frac{c^2}{4}\cdot 2{sin {15}^{\circ }{cos {15}^{\circ }=\frac{c^2}{4}{sin {30}^{\circ }=\frac{c^2}{4}\cdot \frac{1}{2}=\frac{36}{8}=4,5.\ }\ }\ }\ }\ }$

Ответ: 4,5

4. В лифт 11-этажного бизнес-центра на 1 этаже входят 4 человека. Предположим, что каждый из них может выйти на любом этаже, начиная со второго. Найдите вероятность того, что все они выйдут на разных этажах.

Решение:

Первый из этих людей может выйти на любом из 10 этажей (со второго до 11-го).

Для того чтобы все четверо вышли на разных этажах, необходимо, чтобы второй человек вышел на любом этаже, кроме того, на котором вышел первый. Вероятность этого события равна 9/10.

Аналогично, третьему надо выйти на любом из оставшихся 8 этажей. Вероятность этого события 8/10.

Для четвертного человека вероятность выйти на таком этаже, на котором не вышел никто из троих, равна 7/10.

Вероятность одновременного наступления этих событий равна произведению вероятностей, то есть 0,9 * 0,8 * 0,7 = 0,504.

Ответ: 0,504

5. Анна Малкова Решите уравнение $(x+1)\ (x+2)\ (x+3)\ (x+4\ )\ =\ 3$

В ответе запишите сумму действительных корней уравнения.

Решение:

Группируем множители:
$\left(\left(x+1\right)\left(x+4\right)\right)\cdot \left(\left(x+2\right)\left(x+3\right)\right)=3$

$\left(x^2+5x+4\right)\cdot \left(x^2+5x+6\right)=3;$

Замена $x^2+5x+4=t;$

$t\left(t+2\right)=3;$

$t^2+2t-3=0;$

$t=1$ или $t=-3;$

$\left[\begin{array}{c}{x^2+5x+4=1} \\ {x^2+5x+4=-3}\end{array}\right.;\left[\begin{array}{c}{x^2+5x+3=0} \\ {x^2+5x+7=0}\end{array};\right.$

Во втором уравнении $D \textless 0,$ нет корней.

Уравнение $x^2+5x+3=0$ имеет 2 корня. По теореме Виета, их сумма равна -5.

Ответ: -5

6. Биссектрисы смежных углов параллелограмма АВСD пересекают сторону ВС в точке Е. Найдите угол АЕD. Ответ выразите в градусах.

Решение:

Углы А и D – односторонние при параллельных прямых AB и CD и секущей AD. Сумма односторонних углов равна $180^\circ$ .

$\angle A+\angle D={180}^{\circ };$

Пусть $\angle A=2 \alpha ,\ \angle D=2 \varphi ,$

$2 \alpha +2 \varphi ={180}^{\circ },$

$\alpha + \varphi ={90}^{\circ },$

Рассмотрим $\triangle AED,\ \angle AED={180}^{\circ } \alpha - \varphi ={90}^{\circ }.$

Ответ: 90

7. На рисунке изображён график дифференцируемой функции

$y=f\left(x\right),$ определённой на интервале (−10; 3). Найдите количество решений уравнения $f$ на отрезке [−7,5; −2,5].

Слово «дифференцируемая» в условии задачи означает, что у функции $y=f\left(x\right)$ существует производная в каждой точке интервала (−10; 3). Производная функции равна нулю в точках максимума и минимума. На отрезке [−7,5; −2,5] есть три таких точки. Они отмечены на рисунке.

Ответ: 3

8. В правильной шестиугольной пирамиде SABCDEF ребро основания равно 3, апофема SH равна 4. Найдите боковой поверхности пирамиды.

Решение:

Площадь боковой поверхности пирамиды равна сумме площадей всех боковых граней, и это в 6 раз больше, чем площадь одной грани.

$CD=3$ ,

$\displaystyle SH=4, \, \, \, S_{\triangle SCD}=\frac{1}{2}\cdot 3\cdot 4=6,$

Ответ: 36

9. Ольга Чемезова

Найдите значение выражения $\displaystyle \frac{3{lg 2\ }-{lg 24\ }}{{lg 3\ }\ +{lg 27\ }}$

$\displaystyle \frac{3{lg 2\ }-{lg 24\ }}{{lg 3\ }\ +{lg 27\ }}=\frac{{lg 8-{lg 24\ }\ }}{{lg 81\ }}=\frac{{lg \frac{1}{3}\ }}{{lg 81\ }}={{log}_{81} \frac{1}{3}\ }$ (по формуле перехода к новому основанию: ${{log}_a b\ }=\frac{{{log}_c b\ }}{{{log}_c a\ }}$ )

$\displaystyle {{log}_{81} \frac{1}{3}=\frac{{{log}_3 \frac{1}{3}\ }}{{{log}_3 81\ }}=\frac{-1}{4}=-0,25.\ }$

Ответ: -0,25

10. Груз массой 0,25 кг колеблется на пружине со скоростью, меняющейся по закону $v\left(t\right)=1,6{cos \pi t\ }$ , где t– время в секундах. Кинетическая энергия груза вычисляется по формуле $\displaystyle E=\frac{mv^2}{2}$ , где m – масса груза (в кг), v – скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее $2,4\cdot {10}^{-1}$ Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.

Решение:
$E\ge 2,4\cdot {10}^{-1};$

$\displaystyle E=\frac{mv^2}{2}=\frac{0,25}{2}\cdot {(1,6{cos \pi t)\ }}^2=\frac{1}{8}\cdot {1,6}^2\cdot {{cos}^2 \pi t\ };$

$\displaystyle \frac{1}{8}\cdot \frac{{16}^2}{{10}^2}{cos}^2 \pi t\ge \frac{2,4}{10};$

$\displaystyle {cos}^2 \pi t\ge \frac{3}{4};$
По формуле понижения степени,

$\displaystyle {cos}^2 \pi t=\frac{cos2 \pi t+1}{2}.$ Отсюда
$\displaystyle cos2 \pi t\ge \frac{1}{2}.$
Построим график функции $y=cos2 \pi t$ при $t\ \in \ [0;1]$

$cos0=1$ (при t=0)

$cos2 \pi =1$ (при t=1)

$cos \pi =-1$ (при $\displaystyle t=\frac{1}{2}$ )

$\displaystyle cos\frac{ \pi }{2}=0$ (при $\displaystyle t=\frac{1}{4}$ )

$\displaystyle cos\frac{ \pi }{3}=\frac{1}{2}$ (при $\displaystyle t=\frac{1}{6}$ )

$\displaystyle cos\frac{5 \pi }{3}=\frac{1}{2}$ (при $\displaystyle t=\frac{5}{6}$ )

Найдем, какую часть из первой секунды выполняется неравенство $\displaystyle cos2 \pi t\ge \frac{1}{2}.$

Получим, что $\displaystyle cos \pi t\ge \frac{1}{2}$ при $t\ \in [0;1]$ на $\displaystyle 0\le t\le \frac{1}{6}$ и $\displaystyle \frac{5}{6}\le t\le 1.$

Вместе эти отрезки составляют $\displaystyle \frac{1}{3}$ от первой секунды; $\displaystyle \frac{1}{3}\approx 0,33$

Ответ: 0,33.

11. Имеется два куска сплава массами 7 кг и 42 кг с различным процентным содержанием серебра. От каждого из них взяли по куску равной массы x. Каждый из кусков массой x был сплавлен с остатком другого куска, после чего процентное содержание серебра в обоих сплавах стало одинаковым. Найдите x.

Решение:

Пусть p – доля серебра в первом куске сплава, $0\le p\le 1;$ q – доля серебра во втором куске, $0\le q\le 1;$

В куске массой x, взятом из первого сплава, xp кг серебра.

Когда этот кусок сплавили с остатком второго сплава, получили:

$xp+\left(42-x\right)\cdot q$ – количество серебра в первом получившемся новом сплаве, масса этого сплава 42 кг. Аналогично, во втором новом сплаве (масса которого 7кг) содержится $qx+\left(7-x\right)\cdot p$ кг серебра.

Так как процентное содержание серебра в получившихся сплавах одинаково, доля серебра (отношение массы серебра к массе сплава) в них тоже одинакова.

Получим:
$\displaystyle \frac{xp+\left(42-x\right)q}{42}=\frac{xq+\left(7-x\right)p}{7}$

$xp+\left(42-x\right)q=6xq+6p\left(7-x\right)$

$xp+42q-xq=6xq+42p-6xp$

$x\left(p-q\right)=6x\left(q-p\right)+42\left(p-q\right)$

$7x\left(p-q\right)=42\left(p-q\right);$

По условию, $p\ne q,$ тогда $7x=42,\ x=6.$

Ответ: 6

12. Найдите наибольшее значение функции $y=17\ x-17\ tg\ x-11$ на отрезке $\displaystyle \left[0;\frac{ \pi }{4}\right]$

Решение:

$\displaystyle y$ если ${{cos}^2 x\ }=1;$

Если $\displaystyle x\in \left[0;\frac{ \pi }{4}\right],$ то ${cos x=1\ }$ при $x=0,$

Найдём $\displaystyle y$

$\displaystyle y$

$y\left(x\right)$ убывает при $\displaystyle x\in \left[0;\frac{ \pi }{4}\right];$

$y_{max}=y\left(0\right)=-11.$

Ответ: - 11

Часть 2. Задания с развернутым ответом

13. Анна Малкова

а) Решите уравнение $\sqrt{{cos x\ }} \cdot (3tgx-2{cos x)=0\ }$

б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[6;9\right]$

$\sqrt{{cos x\ }} \cdot (3tgx-2{cos x)=0\ }\Leftrightarrow \left\{ \begin{array}{c}{cos x\ge 0\ } \\{cos x\ne 0\ } \\\left[\begin{array}{c}{{cos x=0\ }} \\ {3tgx=2{cos x\ }}\end{array}\right. \end{array}\Leftrightarrow \left\{ \begin{array}{c}{cos x \textgreater 0\ } \\3{sin x=2{{cos}^2 x\ }\ } \end{array}\right.\right.$

Решим уравнение $2{{cos}^2 x\ }=3{sin x\ }$

$2-2{{sin}^2 x=3{sin x;\ }\ }$

Замена

${sin x=t,\ }$

$-1\le t\le 1;$

$2t^2+3t-2=0;$

$\displaystyle D=25;t=\frac{-3\pm 5}{4};$

$\displaystyle \left[\begin{array}{c}{t_1=-2;\ } \\ {t_2= \displaystyle \frac{1}{2};\ }\end{array}\right.$

Если $t_1 = -2; \, sin x= -2$ - нет решений

Если $t_2 = \frac{1}{2} \, sin x = \frac{1}{2}.$

Получим:

$\displaystyle \left\{ \begin{array}{c}{sin x=\frac{1}{2}\ } \\{cos x \textgreater 0\ } \end{array}\right.\Leftrightarrow \begin{array}{c}{x=\frac{ \pi }{6}+2 \pi n,\ n\in Z} \\ {\begin{array}{c}\\ \end{array}}\end{array}$

б) Найдём корни на отрезке [6;9].

Заметим, что

$\displaystyle\frac{3\pi}{2}\textless 6 \textless 2\pi$

$2\pi \textless 9 \textless 3\pi$

На отрезке [6;9] находится единственный корень

$\displaystyle x=2 \pi +\frac{ \pi }{6}=\frac{13 \pi }{6}.$

Ответ: а) $\displaystyle \frac{ \pi }{6}+2 \pi n,\ n\in Z$

б) $\displaystyle \frac{13 \pi }{6}$

14. Анна Малкова В правильной треугольной призме $ABCA_1B_1C_1$ точки М и N – середины ребер АС и ВС соответственно, точка К – середина бокового ребра $CC_1.$

а) Докажите, что линия пересечения плоскостей АВК и $MNC_1$ параллельна одному из ребер основания

б) Найдите угол между плоскостями АВК и $MNC_1,$ если $AB\ =\ 4, AA_1\ =6.$

Решение:

а) $MN\parallel AB$ как средняя линия $\triangle ABC\Rightarrow MN\parallel \left(ABK\right)$ по признаку параллельности прямой и плоскости;
$MN\in \left(C_1MN\right);$
$\left(C_1MN\right)\cap \left(ABK\right)=PQ,$
$PQ\parallel MN$ по теореме о прямой и параллельной ей плоскости, тогда $PQ\parallel AB.$

б) Найдём $\varphi$ – угол между $\left(ABK\right)$ и $\left(C_1MN\right).$

Пусть H – середина AB, G – середина MN, E – середина PQ.

$C_1N$ и $BK$ – медианы $\triangle BC_1C;$

$\displaystyle \frac{C_1Q}{QN}=\frac{2}{1};\frac{BQ}{QK}=\frac{2}{1};$ - по свойству медиан треугольника.

$\displaystyle C_1Q=\frac{2}{3}CN;QK=\frac{1}{3}BK$

$\triangle KEQ\sim \triangle KHB;$ $\triangle C_1EQ\sim \triangle C_1GN_1,$ по двум углам, тогда

$\displaystyle C_1E=\frac{2}{3}C_1G;EK=\frac{1}{3}HK$

По условию, $AB=4,\ AA_1=6,$

$\displaystyle HC=\frac{4\sqrt{3}}{2}=2\sqrt{3},\ GC=\frac{1}{2}HC=\sqrt{3}$ (из $\triangle ABC$ ),

$\displaystyle C_1G=\sqrt{3+6^2}=\sqrt{39}$ (из $\triangle C_1CG$ ),

$\displaystyle C_1E=\frac{2}{3}\sqrt{39;}$

$\displaystyle C_1K=\frac{1}{2}C_1C=3,$

$HK=\sqrt{12+9}=\sqrt{21}$ из $\triangle CHK,$

$\displaystyle EK=\frac{1}{3}HK=\frac{\sqrt{21}}{3}$

Рассмотрим $\triangle C_1EK.$

По теореме косинусов для $\triangle C_1EK,$

$\displaystyle 9=\frac{4}{9}\cdot 39+\frac{21}{9}-\frac{2}{3}\cdot \frac{2}{3}\sqrt{39}\cdot \sqrt{21}\cdot {cos \varphi \ }$

$\displaystyle 9=\frac{4\cdot 13}{3}+\frac{7}{3}-\frac{4}{3}\sqrt{13}\cdot \sqrt{7}{cos \varphi }$
$27=52+7-4\sqrt{13}\cdot \sqrt{7}{cos \varphi \ }$

$4\sqrt{91}{cos \varphi =32\ }$

$\sqrt{91}{cos \varphi =8\ }$

$\displaystyle {cos \varphi =\frac{8}{\sqrt{91}}\ }$

15. Решите неравенство:
${{{{{(log}^2}_2 x\ }-2log}_2 x)^2\ }+36{{{log}^{\ }}_2 x+45\ } \textless 18{{{log}^2}_2 x\ }$

Решение
${\left({{log}^2_2 x-2{{log}_2 x\ }\ }\right)}^2+36\cdot {{log}_2 x\ }+45 \textless 18{{log}^2_2 x\ }$

Замена ${{log}_2 x\ }=t,$

${\left(t^2-2t\right)}^2+36t+45 \textless 18t^2$

${\left(t^2-2t\right)}^2 \textless 18t^2-36t-45$

${\left(t^2-2t\right)}^2 \textless 9\left(2t^2-4t-5\right)$

Сделаем ещё одну замену: $t^2-2t=z,$ получим:

$z^2 \textless 9\left(2z-5\right);$

$z^2-18z+45 \textless 0$

Найдем корни уравнения $z^2-18z-45=0$

$D={18}^2-4\cdot 45=324-180=144$

$\displaystyle z=\frac{18\pm 12}{2}; \, z_1=15,\ z_2=3$

$\left(z-15\right)\left(z-3\right) \textless 0$

$3 \textless z \textless 15.$

Вернемся к переменной t:

$3 \textless t^2-2t \textless 15$

$\left\{ \begin{array}{c}t^2-2t-3 \textgreater 0 \\t^2-2t-15 \textless 0 \end{array}\right.$

$\left\{ \begin{array}{c}\left(t+1\right)\left(t-3\right) \textgreater 0 \\\left(t-5\right)\left(t+3\right) \textless 0 \end{array}\right.$

$\left[\begin{array}{c}{-3 \textless t \textless -1} \\ {3 \textless t \textless 5}\end{array}\right.$

Вернемся к переменной х:

$\left[\begin{array}{c}{-3 \textless {{log}_2 x\ } \textless -1} \\ {3 \textless {{log}_2 x\ } \textless 5}\end{array}\right.$

Логарифмическая функция по основанию 2 монотонно возрастает, и если $log_2x_1 \textless log_2x_2,$ то $x_1 \textless x_2.$ Получим:

$\left[\begin{array}{c}{\displaystyle \frac{1}{8} \textless x \textless \frac{1}{2}} \\ {8 \textless x\textless 32}\end{array}\right.$

Ответ: $\displaystyle x\in \left(\frac{1}{8};\frac{1}{2}\right)\cup \left(8;32\right)$

16. Анна Малкова

В треугольнике АВС угол С – прямой. Биссектриса угла А пересекает окружность с центром О, описанную вокруг треугольника АВС, в точке М.

а) Докажите, что ОМ параллельна одной из сторон треугольника АВС.

б) Найдите площадь четырехугольника АОМС, если угол АВС равен $75^\circ, OM = 6.$

Решение:

а) Докажем, что $OM\parallel AC$

Пусть $\angle A = 2 \varphi, \, \angle CAM = \angle BAM = \varphi,$

Треугольник АОМ – равнобедренный, ОА = ОМ как радиусы окружности. Тогда $\angle AMO = \angle OAM = \varphi$ .
Мы получили:

$\angle CAM=\angle AMO$ Эти углы - накрест лежащие, следовательно, $OM\parallel AC.$

б) Найдем $S_{AOMC},$ если $\angle AB={75}^{\circ },\angle A={15}^{\circ },\ OM=6$

AOMC - трапеция, $OM \parallel AC,$

$R=6,\ AB=12$

Из треугольника АВС:

$AC=AB cos\ {15}^{\circ }$

Высота трапеции $\displaystyle h=HC = \frac{1}{2}BC,$ т.к. OH – средняя линия $\triangle ABC;$
$BC=AB{sin {15}^{\circ },\ }$

$\displaystyle h=HC=\frac{ABsin\ {15}^{\circ }}{2}.$

$\displaystyle S_{AOMC}=\frac{OM+AC}{2}\cdot h=\frac{6+12{cos {15}^{\circ }\ }}{2}\cdot \frac{12{sin {15}^{\circ }\ }}{2}=$

$=6\left(3+6{cos {15}^{\circ }\ }\right){sin {15}^{\circ }=18{sin {15}^{\circ }+36{sin {15}^{\circ }{cos {15}^{\circ }=\ }\ }\ }\ }$

$=18{sin {15}^{\circ }+18{sin {30}^{\circ }=18{sin {15}^{\circ }+9=9\left(1+2{sin {15}^{\circ }\ }\right)\ }\ \ }\ }$

Найдем, чему равен $sin15^\circ$

$\displaystyle {cos {30}^{\circ }=\frac{\sqrt{3}}{2}=1-2{{sin}^2 {15}^{\circ }\ }\ }$

$\displaystyle {{sin}^2 {15}^{\circ }=\frac{1-{cos {30}^{\circ }\ }}{2}=\frac{1-\frac{\sqrt{3}}{2}}{2}=\frac{2-\sqrt{3}}{4}\ }$

$\displaystyle {sin {15}^{\circ }=\frac{\sqrt{2-\sqrt{3}}}{2}\ }$

$S=9\sqrt{2-\sqrt{3}}+9=9\left(\sqrt{2-\sqrt{3}}+1\right)$

Ответ: $9(\sqrt{2-\sqrt{3}}+1)$

17. В июле 2017 года планируется взять кредит в банке в размере S тыс. рублей, где S – натуральное число, на 3 года. Условия его возврата таковы

− каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Месяц и год	Июль 2017	Июль 2018	Июль 2019	Июль 2020
Долг (в тыс. рублей)	S	0,7S	0,4S	0

Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей. Ответ дайте в тысячах рублей.

Нарисуем схему погашения кредита.

По условию, каждая из выплат – целое число тысяч рублей.

Первая выплата: $\displaystyle 1,15S-0,7S=0,45S=\frac{9}{20}S$

Вторая выплата: $\displaystyle 1,15\cdot 0,7S-0,4S=0,405S=\frac{81}{200}S$

Третья выплата: $\displaystyle 1,15\cdot 0,4S=0,46S=\frac{23}{50}S$

По условию, $\displaystyle \frac{9}{20}S, \ \frac{81}{200}S$ и $\displaystyle \frac{23}{50}S$ – целые числа. Это значит, что $S\vdots 20;\ \ \ \ S\vdots 200$ и $S\vdots 50$ , то есть $S\vdots 200.$

Наименьшее возможное S равно 200 (тысяч рублей).

Ответ: 200

18. Найдите все значения параметра а, при которых система уравнений
$\left\{ \begin{array}{c}{\left(5-2\sqrt{6}\right)}^x+{\left(5+2\sqrt{6}\right)}^x-5a=y-\left|y\right|-8, \\x^2-\left(a-4\right)y=0 \end{array}\right.$

имеет единственное решение

Решение:

Заметим, что $\displaystyle 5-2\sqrt{6}=\frac{1}{5+2\sqrt{6}}$ , так как $(5- 2\sqrt{6})\cdot(5+2\sqrt{6})=25-24=1.$

Получим:

$\displaystyle \left\{ \begin{array}{c}{\left(5+2\sqrt{6}\right)}^x+\frac{1}{{\left(5+2\sqrt{6}\right)}^x}-5a=y-\left|y\right|-8 \\x^2-\left(a-4\right)y=0 \end{array}\right.$

Система четна относительно x, т.к. $\displaystyle \frac{1}{{\left(5+2\sqrt{6}\right)}^x}={\left(5+2\sqrt{6}\right)}^{-x}$ –уравнения не меняются при замене x на -x.

Если $\left(x_0;y_0\right)$ – решение, то $\left(-x_0,y_0\right)$ – тоже решение. Единственное решение система может иметь, только если $x_0=0.$

Подставим в уравнения системы $x_0=0$ , получим:

$\left\{ \begin{array}{c}2-5a=y-\left|y\right|-8 \\\left(4-a\right)y=0 \end{array}\right.$

$\left\{ \begin{array}{c}2-5a=y-\left|y\right|-8 \\\left[\begin{array}{c}{a=4} \\ {y=0}\end{array}\right. \end{array}\right.$

1) Если $y=0,$ то $2-5a=-8,$ $a=2.$

2) Если $a=4,$ то

$2-20=y-\left|y\right|-8$

$y-\left|y\right|=-10;$

$\left|y\right|-y=10$

Раскрыв модуль по определению, решим это уравнение:

$\left[\begin{array}{c}{\left\{ \begin{array}{c}y\ge 0 \\0=10 \end{array}\right.\ \ \ \o} \\ {\left\{ \begin{array}{c}y \textless 0 \\-2y=10,\ y=-5 \end{array}\right.}\end{array}\right.$

Значит, $y= -5$ – единственное решение при $a = 4.$

Подставим по очереди $a=2$ и $a=4$ в исходную систему уравнений.

При $a=2.$

$\left\{ \begin{array}{c}{\left(5-2\sqrt{6}\right)}^x+{\left(5+2\sqrt{6}\right)}^x-10=y-\left|y\right|-8 \\x^2+2y=0 \end{array}\right.$

$\left\{ \begin{array}{c}{\left(5+2\sqrt{6}\right)}^x+{\left(5+2\sqrt{6}\right)}^{-x}=y-\left|y\right|+2 \\x^2+2y=0 \end{array}\right.$

Из второго уравнения: $2y=-x^2;y\le 0$

Если y=0, то x=0, $\left(0;0\right)$ – решение.

Если $y \textless 0,$ то $\left|y\right|=-y,$ тогда

${\left(5+2\sqrt{6}\right)}^x+{\left(5+2\sqrt{6}\right)}^{-x}=-x^2+2.$

Покажем, что уравнение не имеет других решений, кроме $x=0.$

Правая часть: $-x^2+2=2-x^2\leq2.$

Левая часть: $(5+2\sqrt{6})^x+(5+2\sqrt{6})^{-x};$

Обозначим $5+2\sqrt{6}=a, \, \, a \textgreater 1.$

Левая часть уравнения имеет вид:

$a^x+a^{-x}.$

Покажем, что $a^x+a^{-x} \geq 2,$ то есть $\displaystyle a^x+\frac{1}{a^x} \geq 2.$

Домножим обе части на $a^x \textgreater 0;$

$a^{2x}-2\cdot a^x+1\geq 0;$

$(a^x-1)\geq 0$ - верно для всех x.

Значит, $(5+2\sqrt{6})^x+(5+2\sqrt{6})^{-x} \leq 2,$

Уравнение имеет единственное решение, если

$(5+2\sqrt{6})^x+(5+2\sqrt{6})^{-x}=2-x^2=2;$

Тогда $x=0$

Мы получили, что при $a = 2$ единственное решение системы – пара чисел (0; 0).

При $a=4$

$\left\{ \begin{array}{c}{\left(5+2\sqrt{6}\right)}^x+{\left(5+2\sqrt{6}\right)}^{-x}=y-\left|y\right|+12 \\x=0 \end{array}\right.$

Тогда

$2=y-\left|y\right|+12$

$y-\left|y\right|+10=0$

$y \textless 0,$ тогда

$2y+10=0,\ y=-5; \left(0;-5\right)$ – единственное решение.

Ответ: $a=2$ или $a=4.$

19. На окружности некоторым образом расставили натуральные числа от 1 до 21 (каждое число поставлено по одному разу). Затем для каждой пары соседних чисел нашли разность большего и меньшего.

а) Могли ли все полученные разности быть не меньше 11?

б) Могли ли все полученные разности быть не меньше 10?

в) Помимо полученных разностей, для каждой пары чисел, стоящих через одно, нашли разность большего и меньшего. Для какого наибольшего целого числа k можно так расставить числа, чтобы все разности были не меньше k?

а) Выпишем наши числа в ряд:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21.

Число 11 находится ровно посередине этой последовательности чисел. Модуль разности числа 11 и любого из оставшихся чисел не больше 10. Значит, при любой расстановке чисел на окружности все разности соседних чисел не могут быть больше или равны 11.

б) Да, это возможно. Вот пример:

Расставим числа по окружности в следующем порядке:

1, 12, 2, 13, 3, 14, 4, 15, 5, 16, 6, 17, 7, 18, 8, 19, 9, 20, 10, 21, 11.

Легко видеть, что любое число на окружности здесь отличается от соседнего не меньше чем на 10.

в) Еще раз выпишем наши числа в ряд.

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21.

Всего их 21. Разобьем их на три группы по 7 чисел.

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21.

Если числа из одной группы оказались на окружности рядом (или через одно), то их разность не больше 6.

Расставим числа на окружности так, что каждое третье число будет из первой группы.

Куда бы мы ни поставили число 8 – рядом с ним или через одно от него будет находиться число из первой группы. Тогда одна из соответствующих разностей не больше 6. Значит, все разности не могут быть равны 7 или быть больше 7.

Как бы мы ни расставляли числа на окружности, найдется разность (либо между соседними, либо между стоящими через одно), которая меньше или равна 6.

Значит, $k\le 6.$

Приведем пример, когда k=6.

Сначала расставим числа из первой группы (от 1 до 7), оставив между каждыми из них два свободных места. Затем числа из второй группы и из третьей:

1, 8, 15, 2, 9, 16, 3, 10, 17, 4, 11, 18, 5, 12, 19, 6, 13, 20, 7, 14, 21

Получили, что наибольшее значение k равно 6.

Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Вариант 4, решения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 26.09.2023

Вариант 4, решения

Это полезно