Вариант 4

Часть 1. Задания с кратким ответом

1. Автомобиль увеличил скорость на 150%. На сколько процентов меньше времени ему потребуется теперь для прохождения того же расстояния?

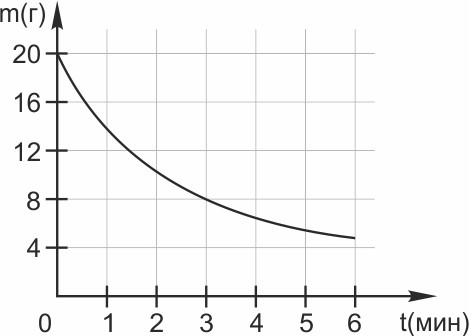
2. В ходе химической реакции количество исходного вещества (реагента), которое еще не вступило в реакцию, со временем постепенно уменьшается. На рисунке эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат – масса оставшегося реагента, который еще не вступил в реакцию (в граммах). Определите по графику, сколько граммов реагента вступило в реакцию за три минуты?

3. Анна Малкова Найдите площадь прямоугольного треугольника, если его гипотенуза равна 6, а острый угол равен $15{}^\circ.$

4. В лифт 11-этажного бизнес-центра на 1 этаже входят 4 человека. Предположим, что каждый из них может выйти на любом этаже, начиная со второго. Найдите вероятность того, что все они выйдут на разных этажах.

5. Анна Малкова Решите уравнение $(x+1)\ (x+2)\ (x+3)\ (x+4\ )\ =\ 3$

В ответе запишите сумму действительных корней уравнения.

6. Биссектрисы смежных углов параллелограмма АВСD пересекают сторону ВС в точке Е. Найдите угол АЕD. Ответ выразите в градусах.

7. На рисунке изображён график дифференцируемой функции

$y=f\left(x\right),$ определённой на интервале (−10; 3). Найдите количество решений уравнения $f$ на отрезке [−7,5; −2,5].

8. В правильной шестиугольной пирамиде SABCDEF ребро основания равно 3, апофема SH равна 4. Найдите боковой поверхности пирамиды.

9. Ольга Чемезова

Найдите значение выражения $\displaystyle \frac{3{lg 2\ }-{lg 24\ }}{{lg 3\ }\ +{lg 27\ }}$

10. Груз массой 0,25 кг колеблется на пружине со скоростью, меняющейся по закону $v\left(t\right)=1,6{cos \pi t\ }$ , где t– время в секундах. Кинетическая энергия груза вычисляется по формуле $\displaystyle E=\frac{mv^2}{2}$ , где m – масса груза (в кг), v – скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее $2,4\cdot {10}^{-1}$ Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.

11. Имеется два куска сплава массами 7 кг и 42 кг с различным процентным содержанием серебра. От каждого из них взяли по куску равной массы x. Каждый из кусков массой x был сплавлен с остатком другого куска, после чего процентное содержание серебра в обоих сплавах стало одинаковым. Найдите x.

12. Найдите наибольшее значение функции $y=17\ x-17\ tg\ x-11$ на отрезке $\displaystyle \left[0;\frac{ \pi }{4}\right]$

Часть 2. Задания с развернутым ответом

13. Анна Малкова

а) Решите уравнение $\sqrt{{cos x\ }} \cdot (3tgx-2{cos x)=0\ }$

б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[6;9\right]$

14. Анна Малкова В правильной треугольной призме $ABCA_1B_1C_1$ точки М и N – середины ребер АС и ВС соответственно, точка К – середина бокового ребра $CC_1.$

а) Докажите, что линия пересечения плоскостей АВК и $MNC_1$ параллельна одному из ребер основания

б) Найдите угол между плоскостями АВК и $MNC_1,$ если $AB\ =\ 4, AA_1\ =6.$

15. Решите неравенство:
${{{{{(log}^2}_2 x\ }-2log}_2 x)^2\ }+36{{{log}^{\ }}_2 x+45\ } \textless 18{{{log}^2}_2 x\ }$

16. Анна Малкова

В треугольнике АВС угол С – прямой. Биссектриса угла А пересекает окружность с центром О, описанную вокруг треугольника АВС, в точке М.

а) Докажите, что ОМ параллельна одной из сторон треугольника АВС.

б) Найдите площадь четырехугольника АОМС, если угол АВС равен $75^\circ, OM = 6.$

17. В июле 2017 года планируется взять кредит в банке в размере S тыс. рублей, где S – натуральное число, на 3 года. Условия его возврата таковы

− каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Месяц и год	Июль 2017	Июль 2018	Июль 2019	Июль 2020
Долг (в тыс. рублей)	S	0,7S	0,4S	0

Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей. Ответ дайте в тысячах рублей.

18. Найдите все значения параметра а, при которых система уравнений
$\left\{ \begin{array}{c}{\left(5-2\sqrt{6}\right)}^x+{\left(5+2\sqrt{6}\right)}^x-5a=y-\left|y\right|-8, \\x^2-\left(a-4\right)y=0 \end{array}\right.$

имеет единственное решение

19. На окружности некоторым образом расставили натуральные числа от 1 до 21 (каждое число поставлено по одному разу). Затем для каждой пары соседних чисел нашли разность большего и меньшего.

а) Могли ли все полученные разности быть не меньше 11?

б) Могли ли все полученные разности быть не меньше 10?

в) Помимо полученных разностей, для каждой пары чисел, стоящих через одно, нашли разность большего и меньшего. Для какого наибольшего целого числа k можно так расставить числа, чтобы все разности были не меньше k?

Скачать вариант в .pdf

Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Вариант 4» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 06.09.2023

Вариант 4

Это полезно