Видеоразбор варианта 6:
Часть 1. Задания с кратким ответом
1. Расстояние между Москвой и Смоленском по железной дороге равно 415 км. На этом пути расположены города Можайск и Вязьма. Расстояние между Москвой и Можайском относится к расстоянию между Можайском и Вязьмой как 7 : 9, а расстояние между Можайском и Вязьмой составляет 27/35 расстояния между Вязьмой и Смоленском.
Найдите расстояние от Москвы до Можайска. Ответ выразите в километрах.
Решение:
По условию, \(x+y+z=415,\ \) \(\displaystyle \frac{x}{y}=\frac{7}{9};\) \(\displaystyle x=\frac{7}{9}y;\) \(\displaystyle \frac{y}{z}=\frac{27}{35};\) \(\displaystyle y=\frac{27}{35}z;\)
Тогда \(\displaystyle x=\frac{7}{9}\cdot \frac{27}{35}z=\frac{3}{5}z;\)
\(\displaystyle \frac{3}{5}z+\frac{27}{35}z+z=415 \Rightarrow z=35\cdot 5=175,\)
\(\displaystyle x=\frac{3}{5}\cdot 175=3\cdot 35=105\) км
Ответ: 105
2. На рисунке показан график движения автомобиля по маршруту. На оси абсцисс откладывается время (в часах), на оси ординат — пройденный путь (в километрах). Найдите среднюю скорость движения автомобиля на данном маршруте. Ответ дайте в км/ч.
Решение:
Средняя скорость находится по формуле:
Ответ: 50.
3. В равнобедренном треугольнике АВС боковые стороны АВ = АС = 25, основание ВС = 14. Найдите расстояние от точки В до стороны АС.
Решение:
Пусть \(BK\bot AC,\) \(AH\bot BC.\)
Высота \(BK\) — расстояние от \(B\) до \(AC\):
В \(\triangle ABH:\)
\(BC=7,\) \(AB=25,\) \(\angle H=90{}^\circ \Rightarrow AH=\sqrt{{25}^2-7^2}=24\) по теореме Пифагора,
\(\displaystyle S_{\triangle ABC}=\frac{1}{2}BC\cdot AH=\frac{1}{2}AC\cdot BK,\)
\(14\cdot 24=25\cdot BK,\)
\(\displaystyle BK=\frac{14\cdot 24}{25}=13,44\)
Ответ: 13,44
4. Анна Малкова Играя в снежки, Маша попадает в цель с вероятностью 0,8, а Наташа — с вероятностью 0,25. Маша и Наташа одновременно бросили снежки в Василия. С какой вероятностью в Василия попадет хотя бы один снежок?
Решение: Найдем вероятность того, что в Василия не попадет ни один снежок, то есть и Маша промахнулась (вероятность этого события 1 — 0,8 = 0,2), и Наташа независимо от нее промахнулась (вероятность этого события 1 — 0,25 = 0,75). Получим:
\(0,2\cdot \ 0,65\ =\ 0,15. \)
Вероятность противоположного события (в Василия попал хотя бы один снежок) равна
1 — 0,15 = 0,85.
Ответ: 0,85
5. Решите уравнение:
\(x^{{lg x\ }}=1000x^2.\)
В ответе запишите сумму корней.
Решение:
ОДЗ: \(x \textgreater 0\)
Возьмем десятичные логарифмы от обеих частей уравнения:
\({lg \left(x^{{lg x\ }}\right)\ }={lg \left(1000x^2\right)\ }\)
\({lg x\ }\cdot {lg x\ }={lg 1000\ }+{lg x^2\ }\)
\({\left({lg x\ }\right)}^2=3+2{lg x\ }\)
Замена: \({lg x\ }=t,\)
\(t^2-2t-3=0,\)
\(t=3\) или \(t=-1,\)
\(\left[ \begin{array}{c}
{lg x\ }=3 \\
{lg x\ }=-1 \end{array}
\right.; \left[ \begin{array}{c}
x=1000 \\
x=0,1 \end{array}
\right.\)
\(x_1+x_2=1000,1.\)
Ответ: 1000,1
6. Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 3, периметр равен 42. Найдите площадь трапеции.
Решение:
\(BC=3, P=42\)
\(\angle CBD=\angle BDA\) — накрест лежащие, тогда \(\triangle ABD\) — равнобедренный, значит, \(AB=AD=CD.\)
Пусть \(AB=AD=CD=x,\) \(BC=3,\) \(3x+3=42,\) \(x=13.\)
Проведем высоты \(BH\) и \(CE;\) \(HE=BC=3,\)
\(\displaystyle AH=ED=\frac{13-3}{2}=5;\) из \(\triangle CED,\)
\(\angle E=90{}^\circ ,\) \(CE=\sqrt{{13}^2-5^2}=12;\)
\(\displaystyle S_{ABCD}=\frac{AD+BC}{2}\cdot CE=\frac{3+13}{2}\cdot 12=96\).
Ответ: 96
7. На рисунке изображен график функции y=f(x). Найдите значение выражения F(7)−F(1), где F(x) - одна из первообразных функции f(x).
Решение: Согласно формуле Ньютона-Лейбница, разность первообразных F(7)−F(1) функции y=f(x) в точках 7 и 1 равна площади фигуры, ограниченной графиком функции, прямыми х = 1 и х = 7 и осью Х.
Площадь этой фигуры равна сумме площадей трапеции с основаниями 1 и 2 и высотой 2 и прямоугольника со сторонами 4 и 2.
Получим: F(7)−F(1) = S = S1 + S2 = 3 + 8 = 11.
Ответ: 11
8. Анна Малкова Снеговик собран из трех снежных шаров, поставленных друг на друга, причем их радиусы относятся как 5 : 3 : 2, а высота снеговика равна 1,5 метра. Найдите массу снеговика (в кг). Шары считать идеальными, число \(\pi \) принять равным 3,14, плотность снега - равной 400 кг/м³. Ответ округлить до целого числа килограммов, объемом морковки пренебречь.
Решение:
\(\displaystyle D_1=0,75=\frac{3}{4}\)
\(\displaystyle D_2=0,3\cdot 1,5=0,45=\frac{45}{100}=\frac{9}{20}\)
\(\displaystyle D_3=0,2\cdot 1,5=0,3=\frac{3}{10}\)
\(\displaystyle V=\frac{4}{3}\cdot \frac{ \pi }{8}\left({\left(\frac{3}{4}\right)}^3+{\left(\frac{9}{20}\right)}^3+{\left(\frac{3}{10}\right)}^3\right)=\frac{4 \pi }{8\cdot 6}\left({\left(\frac{3}{2}\right)}^3+{\left(\frac{9}{10}\right)}^3+{\left(\frac{3}{5}\right)}^3\right)=\)
\(\displaystyle =\frac{ \pi }{48}\cdot \left({\left(\frac{15}{10}\right)}^3+{\left(\frac{9}{10}\right)}^3+{\left(\frac{6}{10}\right)}^3\right)=\frac{ \pi }{48}\cdot \frac{1}{1000}\cdot \left({15}^3+9^3+6^3\right)=\)
\(\displaystyle =\frac{ \pi \cdot 3^3}{48\cdot 1000}\cdot \left(125+27+8\right)=\frac{ \pi \cdot 9}{16\cdot 1000}\cdot \left(125+27+8\right)=\)
\(\displaystyle =\frac{ \pi \cdot 9}{1000\cdot 16}\cdot 160=\frac{ \pi \cdot 9}{100}.\)
\(\displaystyle m=\frac{3,14\cdot 9\cdot 400}{100}=3,14\cdot 36=113,04\approx 113\) кг.
Ответ: 113
9. Вычислите: \(\displaystyle 2-13{cos 2 \alpha \ }+\frac{1}{{sin 2 \alpha \ }}\), если \(tg\ \alpha =-5\)
Решение:
\(tg\ \alpha =t=-5;\)
Согласно формулам универсальной тригонометрической замены,
\(\displaystyle {cos 2 \alpha \ }=\frac{1-t^2}{1+t^2}=\frac{1-25}{1+25}=-\frac{24}{26}=-\frac{12}{13}\)
\(\displaystyle {sin 2 \alpha \ }=\frac{2t}{1+t^2}=-\frac{10}{26}=-\frac{5}{13}\)
\(\displaystyle 2+12-\frac{13}{5}=12-\frac{3}{5}=11,4\)
Ответ: 11,4
10. При температуре \(0^\circ\)С рельс имеет длину \(l_{0}\)=10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону \(l\left(t\right)=l_0(1+\alpha \cdot)\), где \(\alpha =1,2\cdot{10}^{-5}\) — коэффициент теплового расширения, \(\ t\)— температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
Решение:
Зависимость \(l\left(t\right)=l_0(1+ \alpha \cdot t)\) - это функция длины рельса от температуры. Подставим в эту формулу начальные значения: \(l_{0 }\)=10 м и \( \alpha =1,2\cdot {10}^{-5}\). Рельс удлинился на 3 мм, то есть в какой-то момент его длина стала на 3 мм больше. Значит, при определенной температуре длина рельса\(\ l\left(t\right)\) стала равной 10 м + 3 мм.
Переведем миллиметры в метры. Один миллиметр — это одна тысячная часть метра (1мм=0,001м=\({10}^{-3}\) метра).
\(l\left(t\right)=10+3\cdot {10}^{-3}\) (м)
Получим:
\(10+3\cdot {10}^{-3}=10(1+1,2\cdot {10}^{-5}\cdot t)\)
Это линейное уравнение с одной переменной t. Раскроем скобки в правой части
\(10+3\cdot {10}^{-3}=10+12\cdot {10}^{-5}\cdot t\)
Находим t:
\(\displaystyle t=\frac{3\cdot {10}^{-3}}{12\cdot {10}^{-5}}=\frac{1}{4}\cdot {10}^2=\frac{100}{4}=25.\)
При температуре 25 градусов Цельсия рельс удлинится на 3 мм.
Ответ: 25
11. Известно, что внутренние углы некоторого выпуклого многоугольника, наименьший угол которого равен 120 градусов, образуют арифметическую прогрессию с разностью 5 градусов. Определите число сторон этого многоугольника.
Решение:
Пусть \(A_1\) — наименьший угол многоугольника, \(n\) — количество сторон, \(d=5{}^\circ \) - разность арифметической прогрессии.
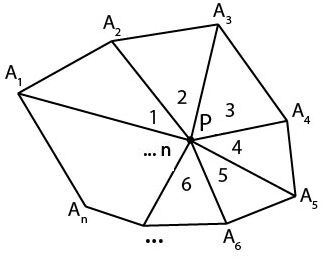
Выведем формулу для суммы углов выпуклого многоугольника. Поставим точку \(P\) внутри многоугольника. Разобьем многоугольника на треугольники с общей вершиной \(P\).
Пронумеруем углы, как показано на рисунке.
Сумма углов n треугольников равна \(180{}^\circ \cdot n.\) С другой стороны, эта сумма равна \(\angle A_1+\angle A_2+\dots +\angle A_n+\angle 1+\angle 2+\dots \angle n.\)
Поскольку \(\angle 1+\angle 2+\angle 3+\dots +n=360{}^\circ ,\) \(\angle A_1+\angle A_2+\dots +A_n+360{}^\circ =180{}^\circ \cdot n.\)
Сумма углов выпуклого многоугольника
\(S=\angle A_1+\angle A_2+\dots \angle A_n=180{}^\circ \cdot n-360{}^\circ =180{}^\circ (n-2)\)
Подставим данные задачи:
\(\displaystyle \frac{2a_1+d\left(n-1\right)}{2}\cdot n=S=180\left(n-2\right)\)
\(\displaystyle \frac{2\cdot 120+5(n-1)}{2}\cdot n=180\left(n-2\right)\)
\(240n+5n^2-5n=360n-720\)
\(5n^2-125n+720=0\)
\(n^2-25n+144=0\)
\(D={25}^2-4\cdot 144=625-576=49\)
\(\displaystyle n=\frac{25\pm 7}{2};\)
\(\left[ \begin{array}{c}
n_1=9 \\
n_2=16 \end{array}
\right.\)
Если \(n=16,\) \(A_{16}=A_1+15d=120+75 \textgreater 180{}^\circ \)
Значит, \(n=9\)
Ответ: 9
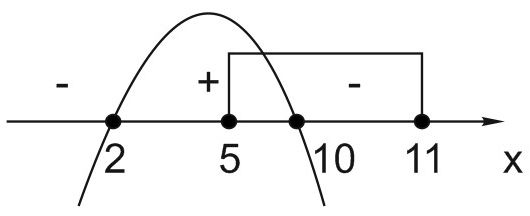
12. Найдите наибольшее значение функции \(y=\left(x^2-10x+10\right)e^{10-x}\) на отрезке \(\left[5;11\right]\).
Решение:
\(y'=\left(-\left(x^2-10x+10\right)+2x-10\right)e^{10-x}\)
Приравняем производную к нулю. Так как \(e^{10-x}\textgreater 0\) всегда, получим:
\(-x^2+10x-10+2x-10=0\)
\(-x^2+12x-20=0\)
\(x^2-12x+20=0\)
\(D=144-80=64\)
\(\displaystyle x_{1,2}=\frac{12\pm 8}{2};\)
\(x_1=10, x_2=2.\)
В точке х = 10 производная меняет знак с «+» на «-», значит, х = 10 – точка максимума.
Наибольшее значение функции на данном отрезке \(y_{max}=y(10)=10.\)
Ответ: 10
Часть 2. Задания с развернутым ответом
13. Ольга Чемезова
а) Решите уравнение \(2{{log}_3 cos\ x\ }={{log}_3 ({sin}^2x+sinx)\ }\)
б) Найдите все корни уравнения на отрезке [-4\(\pi \); 0]
Решение:
\(2{{log}_3 {cos x\ }\ }={{log}_3 \left({{sin}^2 x\ }+{sin x\ }\right)\ }\)
а) ОДЗ
\(\left\{ \begin{array}{c}
{cos x \textgreater 0\ } \\
\ {sin x\ }\left({sin x\ }+1\right) \textgreater 0 \end{array}
\right.\ \ \Longleftrightarrow \ \ \left\{\ \begin{array}{c}
{cos x\ } \textgreater 0 \\
{sin x\ } \textgreater 0 \end{array}
\right.\)
\({{log}_3 {{cos}^2 x\ }\ }={{log}_3 \left({{sin}^2 x\ }+{sin x\ }\right)\ }\)
\({{cos}^2 x\ }={{sin}^2 x\ }+{sin x\ }\)
\(1-{{sin}^2 x\ }={{sin}^2 x\ }+{sin x\ }\)
\(2{{sin}^2 x\ }+{sin x\ }-1=0\)
Сделаем замену \({sin x\ }=t, \; 0 \textless t\le 1\)
\(2t^2+t-1=0\)
\(D=9;\)
\(\displaystyle t=\frac{-1\pm 3}{4};\)
\(\displaystyle t_1=\frac{1}{2};\)
\(t_2=-1\) — не удовлетворяет условию \(0 \textless t\le 1.\)
\(\displaystyle t=\frac{1}{2}; \left\{ \begin{array}{c}
{sin x\ }=\frac{1}{2} \\
{sin x\ } \textgreater 0 \\
{cos x\ } \textgreater 0 \end{array}
\right.\ \Longleftrightarrow \ x=\frac{ \pi }{6}+2 \pi n, n\in Z\)
б) Найдем корни на отрезке \(\left[-4 \pi ;0\right]\)
Это \(\displaystyle \frac{ \pi }{6}-2 \pi =-\frac{11 \pi }{6}\) и \(\frac{ \pi }{6}-4 \pi =-\frac{23 \pi }{6}\)
Ответ: а) \(\displaystyle \frac{ \pi }{6}+2 \pi n,\ n\in Z\);
б) \(-\displaystyle \frac{23 \pi }{6};\) \(\displaystyle -\frac{11 \pi }{6}\)
14. Анна Малкова
В правильном тетраэдре SABC точки М и N — центры граней SAC и SBС соответственно.
а) Докажите, что плоскость, проходящая через точки А, М и N, делит ребро SC пополам.
б) Точка О — центр грани АВС. Найдите расстояние от точки О до плоскости АМN, если ребро тетраэдра равно \(\sqrt{3}.\)
 а) \(M\) и \(N\) — центры граней \(\left(ASC\right)\) и \(\left(BSC\right)\). Пусть \(E\) и \(F\) — середины сторон \(AC\) и \(BC,\) \(M\in SE,\) \(N\in SF.\)
а) \(M\) и \(N\) — центры граней \(\left(ASC\right)\) и \(\left(BSC\right)\). Пусть \(E\) и \(F\) — середины сторон \(AC\) и \(BC,\) \(M\in SE,\) \(N\in SF.\)
\(MN\parallel EF\) (так как \(\triangle SMN\ \sim \ \triangle SEF\)), по углу и двум сторонам, \(EF\) — средняя линия \(\triangle ABC,\) значит, \(EF\parallel AB\) и \(MN\parallel AB\); \(MN\in (AMN)\);
\(\left(AMN\right)\cap \left(ABC\right)=l,\) по теореме о прямой и параллельной ей плоскости, \(l\parallel MN,\) значит, \(B\in l;\)
\(\left(AMN\right)\cap \left(ABC\right)=AB.\)
Пусть \(T\) — середина \(SC.\) Тогда \(AT\) и \(BT\) — медианы \(\triangle ASC\) и \(\triangle BSC;\)
\(N\in BT,\) \(M\in AT,\) значит, \(T\in \left(AMN\right).\)
б) Найдем расстояние от 0 до плоскости \(\left(AMN\right).\)
Пусть \(H\) — середина \(AB,\) \(CH\) — медиана \(\triangle ABC,\) \(O\in CH.\)
\(HT\cap SO=K.\)
Так как \(O\) — проекция \(K\) на \(\left(ABC\right),\) \(OH\bot AB,\) то по теореме о трех перпендикулярах \(KH\bot AB.\)
Тогда плоскость \(THC\bot AB.\)
В плоскости \(THC\) проведем \(OL\bot HT.\)
\(\left. \begin{array}{c}
OL\bot HT \\
OL\bot AB \end{array}
\right\}\Rightarrow OL\bot \left(ABT\right),\) т.е. \(OL\bot \left(AMN\right)\) по признаку перпендикулярности прямой и плоскости.
Рассмотрим \(\triangle THC.\)
Пусть \(Q\) — проекция \(T\) на плоскость \(ABC.\)
Так как \(T\) — середина \(SC,\) \(\triangle TQC\sim \triangle SOC\) по двум углам, \(\displaystyle \frac{QC}{OC}=\frac{TC}{SC}=\frac{1}{2},\) \(Q\) — середина \(OC.\)
Тогда \(HO=OQ=QC,\) т.к. \(O\) — центр грани \(ABC\) \(\displaystyle QT=\frac{1}{2}SO,\) \(\displaystyle OK=\frac{1}{4}SO.\)
\(\displaystyle OL\ =\frac{1}{3}\ CT\ =\frac{a}{6}\)
Ответ: \(\displaystyle \frac{\sqrt{3}}{6}\)
15. Решите неравенство:
\(\displaystyle \frac{1}{{{log}_2 \left(x-1\right)\ }} \textless \frac{1}{{{log}_2 \sqrt{x+1}\ }}\)
Решение:
\(\displaystyle \frac{1}{{{log}_2 \left(x-1\right)\ }} \textless \frac{1}{{{log}_2 \sqrt{x+1}\ }}\)
ОДЗ:
\(\left\{ \begin{array}{c}
x-1 \textgreater 0 \\
x+1\ge 0 \\
x-1\ne 1 \\
\sqrt{x+1}\ne 1 \end{array}
\right.;\)
Упростив эту систему, получим:
\(\left\{ \begin{array}{c}
x \textgreater 1 \\
x\ne 2 \end{array}
\right.\)
\(\displaystyle \frac{1}{{{log}_2 \left(x-1\right)\ }}-\frac{1}{{{log}_2 \sqrt{x+1}\ }} \textless 0\)
\(\displaystyle \frac{{{log}_2 \sqrt{x+1}\ }-{{log}_2 \left(x-1\right)\ }}{{{log}_2 \left(x-1\right)\ }{{log}_2 \sqrt{x+1}\ }} \textless 0\)
По методу замены множителя, множитель \({{log}_h f\ }\) заменяем на \(\left(h-1\right)\left(f-1\right).\)
\({{log}_h f\ }\) - \({{log}_h g\ }\) заменяем на \(\left(h-1\right)\left(f-g\right).\)
С учетом ОДЗ получим:
\(\displaystyle \frac{\sqrt{x+1}-\left(x-1\right)}{\left(x-2\right)\left(\sqrt{x+1}-1\right)} \textless 0, x \textgreater 1, x\ne 2.\)
Сделаем замену: \(\sqrt{x+1}=t.\)
Если \(x \textgreater 1,\) то \(t \textgreater \sqrt{2};\)
\(x\ne 2,\) тогда \(t\ne \sqrt{3}.\)
\(x=t^2-1; x-1=t^2-2.\)
Получим:
\(\displaystyle \left\{ \begin{array}{c}
\begin{array}{c}
\frac{t^2-t-2}{\left(t^2-3\right)\left(t-1\right)} \textgreater 0 \\
t \textgreater \sqrt{2} \end{array}
\\
t\ne \sqrt{3} \end{array}
\right.\)
\(\displaystyle \left\{ \begin{array}{c}
\begin{array}{c}
\frac{\left(t+1\right)\left(t-2\right)}{\left(t^2-3\right)\left(t-1\right)} \textgreater 0 \\
t \textgreater \sqrt{2} \end{array}
\\
t\ne \sqrt{3} \end{array}
\right.\)
\(\displaystyle \left\{ \begin{array}{c}
\begin{array}{c}
\frac{t-2}{t-\sqrt{3}} \textgreater 0 \\
t \textgreater \sqrt{2} \end{array}
\\
t\ne \sqrt{3} \end{array}
\right.\)
\(\left[ \begin{array}{c}
\sqrt{2} \textless t \textless \sqrt{3} \\
t \textgreater 2 \end{array}
\right.\)
\(\left[ \begin{array}{c}
2 \textless \sqrt{x+1} \textless \sqrt{3} \\
\sqrt{x+1} \textgreater 2 \end{array}
\right.\)
\(\left[ \begin{array}{c}
1 \textless x \textless 2 \\
x \textgreater 3 \end{array}
\right.\)
Ответ: \(x\in \left(1;2\right)\cup \left(3;+\infty \right)\)
16. Анна Малкова
а) Окружность с центром Р вписана в треугольник АВС. Биссектриса угла А пересекает окружность, описанную вокруг треугольника АВС, в точке М. Докажите, что треугольник СРМ — равнобедренный.
б) В треугольнике АВС угол С — прямой, АВ = 18. Биссектрисы углов А и В пересекают описанную окружность треугольника АВС в точках М и N соответственно. Найдите МN.
Решение:
Пункт (а) — лемма о трезубце.
Дан треугольник АВС, АМ — биссектриса угла А, Р — центр вписанной окружности треугольника АВС, М — точка пересечения биссектрисы угла А и описанной окружности треугольника АВС. Докажем, что МР = МВ = МС.
Докажем, что МВ = МС = МР.
Вписанные углы ВАМ и ВСМ опираются на дугу ВМ, следовательно, они равны.
Аналогично, вписанные углы САМ и СВМ опираются на дугу СМ, и они тоже равны.
\(\angle BAM=\angle CAM\), поскольку АМ — биссектриса угла ВАС.
Следовательно, \(\angle BCM=\angle BAM=\angle CAM=\angle CBM=\) \(\alpha \) и треугольник ВМС — равнобедренный, ВМ = СМ.
Точка Р — центр вписанной окружности треугольника АВС. Значит, Р — точка пересечения биссектрис треугольника АВС, и тогда ВР и СР — биссектрисы его углов АВС и АСВ соответственно.
Пусть \(\angle BAC=2 \alpha ,\ \ \angle ABC=2 \beta ,\ \ \angle ACB=2 \gamma .\)
Сумма углов треугольника АВС равна 180\({}^\circ\), значит, \(2 \alpha +2 \beta +2 \gamma =180{}^\circ .\)
В треугольнике ВМР: \(\angle PMB=\angle ACB=2 \gamma ,\) \(\angle PBM= \alpha + \beta \). Тогда \(\angle BPM= \alpha + \beta =\angle PBM\), треугольник ВМР равнобедренный, ВМ = РМ. Значит, точка М равноудалена от точек В, С и М.
б)
Про условию, AB=18. Найдем MN.
Согласно лемме о трезубце, \(MC=MB\) и \(NC=NB.\)
Тогда \(M\) — середина дуги \(BC,\) \(N\) — середина дуги \(AC.\)
Сумма дуг \(AC\) и \(BC\) равна \(180{}^\circ .\) Тогда дуга \(\displaystyle \breve{MN}=90{}^\circ =\frac{1}{2}\left(\breve{AC}+\breve{BC}\right)\)
\(\angle MON=90{}^\circ ;\) \(\triangle MON\) — прямоугольный равнобедренный, \(MN=OM\sqrt{2}=R\sqrt{2}=9\sqrt{2}.\)
17. По бизнес-плану предполагается вложить в четырёхлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором общая сумма средств вкладчика за два года станет больше 100 миллионов, а за четыре года станет больше 170 миллионов рублей.
Пусть \(S\).миллионов рублей — первоначальные вложения. К началу 2-го года получится \(1,2S+20\) миллионов рублей, а к началу 3-го года — \(1,2\left(1,2S+20\right)+20=1,44S+44.\) По условию \(1,445+44\ \textgreater \ 100,\) откуда \(\displaystyle S \textgreater \frac{56}{1,44} \textgreater 38,8.\)
К началу 4-го года имеем \(1,2(1,44S+44)+10,\) а в конце проекта
\(1,2(1,2(1,44S-44)+10)+10-2,0736S+63,36+22-2,0736S+85,36.\)
По условию \(2,0736S+85,36 \textgreater 170,\) откуда \(\displaystyle S \textgreater \frac{84,64}{2,0736} \textgreater 40,8.\)
А значит, минимальное возможное целое число, удовлетворяющее условию \(S=41.\)
Ответ: 41 миллион руб.
18. Найдите все значения параметра \(a,\) при которых уравнение
\(25x^5+25\left(a-1\right)x^3-4(a-7)x=0\)
имеет ровно 5 различных решений, а сами решения, упорядоченные по возрастанию, образуют арифметическую прогрессию.
Решение:
\(25x^5+25\left(a-1\right)x^3-4\left(a-7\right)x=0\)
Заметим, что \(x=0\) — решение; разделим на \(x\ne 0,\) чтобы найти другие корни.
\(25x^4+25\left(a-1\right)x^2-4\left(a-7\right)=0 \) (*)
Замена \(x^2=y,\) \(y\ge 0\)
\(25y^2+25\left(a-1\right)y-4\left(a-7\right)=0.\)
Уравнение (*) четно относительно \(x\). Корни исходного уравнения образуют арифметическую прогрессию.
Рассмотрим уравнение
\(25y^2+25\left(a-1\right)y-4\left(a-7\right)=0\)
Его корни: \(y_1=d^2\) (соответствует \(x_1=d\) и \(x_2=-d\));
\(y_2=4d^2\) (соответствует \(x_3=2d\) и \(x_4=-2d\)).
Чтобы уравнение относительно \(y\) имело два различных корня, необходимо выполнение условия \(D \textgreater 0.\) Применим также теорему Виета.
Получим:
\(\displaystyle \left\{ \begin{array}{c}
D \textgreater 0 \\
y_1+y_2=5d^2=\frac{25\left(1-a\right)}{25}=1-a \\
y_1y_2=4d^2=\frac{4\left(7-a\right)}{25} \end{array}
\right.\)
Отсюда:
\(\left\{ \begin{array}{c}
5d^2=1-a \\
25d^4=7-a \end{array}
\right.; \begin{array}{c}
1-a\ge 0 \\
7-a\ge 0 \end{array}
; \)
\({\left(a-1\right)}^2=7-a\)
\(a^2-a-6=0\)
\(\left(a-3\right)\left(a+2\right)=0\)
\(a=3\) — не удовлетворяет условию \(1-a\ge 0\)
При \(a=-2\) все условия выполнены и \(D \textgreater 0.\)
Ответ: \(a=-2.\)
19. В роте два взвода, в первом взводе солдат меньше, чем во втором, но больше чем 50, а вместе солдат меньше чем 120. Командир знает, что роту можно построить по несколько человек в ряд так, что в каждом ряду будет одинаковое число солдат, большее 7, и при этом ни в каком ряду не будет солдат из двух разных взводов.
а) Сколько солдат в первом взводе и сколько во втором? Приведите хотя бы один пример.
б) Можно ли построить роту указанным способом по 11 солдат в одном ряду?
в) Сколько в роте может быть солдат?
Пусть в первом взводе \(a\) солдат, во втором \(b\) солдат, причем \(a\ \textless \ b.\)
В каждом ряду \(k\) солдат.
Перейдем от строгих неравенств к нестрогим. Это полезный прием при решении таких задач.
\(k\ \ge \ 8,\) \(a\ \ge \ 51,\) \(a\ +\ b\ \le \ 119.\) Тогда \(51\ +\ b\ \le \ a\ +\ b\ \le \ 119.\) Отсюда \(51\ +\ b\ \ \le \ 119\) и \(b\ \le \ 68.\)
Получим: \(51\ \le \ a\ \textless \ b\ \le \ 68.\)
Кроме того, \(a\ \vdots k\) и \(b\ \vdots k,\) поскольку ни в одном ряду нет солдат из двух разных взводов.
Заметим, что и 51, и 68 делятся на 17.
а) Пусть в каждом ряду 17 солдат, k = 17. Тогда в первом взводе \(51\ =\ 17\ \cdot\ 3\) солдат, а во втором \(68\ =\ 17\ \ \cdot \ 4\) солдат. Всего в роте равно \(51\ +\ 68\ =\ 119\ \textless \ 120\) солдат, все условия выполнены.
б) Предположим, что \(k\ =\ 11,\) то есть в каждом ряду 11 солдат.
Тогда \(a\) и \(b\) делятся на 11, причем \(a\ \textless \ b.\) Между числами 51 и 68 заключены ровно два числа, которые делятся на 11. Значит, \(a\ =\ 55,\) \(b\ =\ 66.\) Но тогда \(a\ +\ b\ =\ 121\ \textgreater \ 120.\) Мы получили противоречие с условием, и значит, построить роту по 11 человек в ряд в этих условиях нельзя.
в) Построим роту по k человек в ряд, причем \(k\ \ge \ 8.\) Поскольку \(a\) и \(b\) делятся на \(k,\) то и разность \(a\ -\ b\) делится на \(k.\) Но разность \(a\ -\ b\ \le \ 17\) — потому что \(51\ \le \ a\ \textless \ b\ \le \ 68.\)
Значит, \(k\ \le \ 17.\) Нам осталось перебрать варианты от k = 8 до k = 17, учитывая результаты, полученные в пунктах (а) и (б).
1) Если k = 8, то a = 56, b = 64. В роте 56 + 64 = 120 солдат — не подходит по условию задачи.
2) Если k = 9, то a = 54, b = 63, всего в роте 117 солдат — подходит.
3) Случай k = 10 невозможен, так как между числами 51 и 68 найдется только одно число a = 60, которое делится на 10.
4) k = 11 — не подходит, и мы доказали это в пункте (б).
5) k = 12 не подходит, так как между числами 51 и 68 найдется только одно число a = 60, которое делится на 12.
6) k = 13 подходит. Тогда a = 52, b = 65, в роте 52 + 65 = 117 солдат.
7) k = 14 — не подходит, так как между числами 51 и 68 найдется только одно число a = 56, которое делится на 14.
8) k = 15 — не подходит, так как между числами 51 и 68 найдется только одно число a = 60, которое делится на 15.
9) k = 16 — не подходит, поскольку только одно число a = 64 лежит на отрезке [51; 68].
10) k = 17 подходит, мы показали это в пункте (а).
Значит, k = 9, 13 или 17. В роте может быть 117 или 119 солдат.
Ответ: 117 или 119.
В варианте использованы задачи с сайта РешуЕГЭ, из сборников под редакцией М. И. Сканави, Козко, Парфенова и Чирского, а также авторские задачи.