Условие задачи
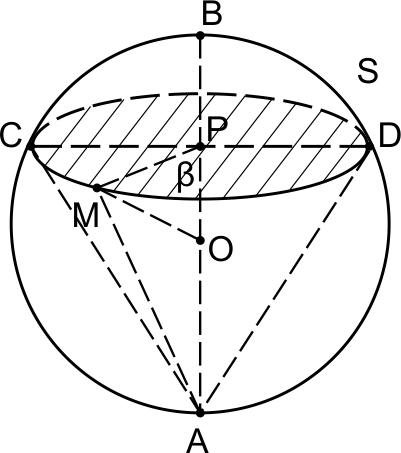
Точка Р лежит на диаметре АВ сферы. При этом АР : РВ = 3 : 1. Через прямую АВ проведена плоскость α, а через точку Р – плоскость β, перпендикулярная АВ. Отрезок СD – общая хорда окружностей сечений сферы этими плоскостями, S – окружность пересечения сферы с плоскостью β, М – точка, лежащая на окружности S.
а) Докажите, что АМ = СD.
б) Найдите объем пирамиды с вершиной М и основанием АВСD, если диаметр сферы равен 12, а М – наиболее удаленная от плоскости α точка окружности S.
Ответ:
б) 108.
Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Ответ. Задание 14, Вариант 5» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена: 16.09.2023
