Решение. Задание 12, Вариант 5

Условие задачи

Найдите наименьшее значение функции $y=(x^2-8x+8)e^{2-x}$ на отрезке [1; 7].

Решение

Хотите решить эту задачу за 10 секунд? Вспомните, что число е – иррациональное. Когда функция $e^t$ принимает целое значение? Очевидно, при t = 0. Если t = 2-x, то х = 2. Именно это значение и надо подставить в формулу функции, чтобы найти ее наименьшее значение. Подставив, получим: у(2) = - 4.

Это решение для хитрых. Мы воспользовались тем, что ответы в первой части ЕГЭ по математике – это целые числа или конечные десятичные дроби. А теперь – честное решение!

$y{}$

Найдем знаки производной на отрезке [1; 7]

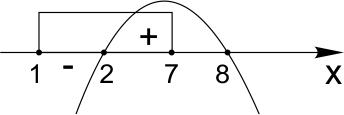
Точка 2 – точка минимума, $y_{min}=-4.$

Ответ:

-4.

Решение. Задание 12, Вариант 5

Это полезно