Условие задачи
Авторская задача. \(\sqrt{2}\begin{vmatrix} sinx \end{vmatrix}=tgx.\)
а) Решить уравнение.
б) Найти все его корни на отрезке \([-3π; 2π].\)
Решение
Начнем с области допустимых значений уравнения: \(cosx\neq 0.\)
Раскроем модуль по определению. Мы помним, что \(\begin{vmatrix}
z
\end{vmatrix}=\left\{\begin{matrix}
z, \ z\geq 0,\\
-z, \ z\leq 0.
\end{matrix}\right. \)
Наше уравнение равносильно совокупности двух систем:
\(\left[\begin{matrix}
\left\{\begin{matrix}
sinx\geq 0, \\\sqrt{2}sinx=tgx,
\end{matrix}\right. \\\left\{\begin{matrix}
sinx< 0, \\-\sqrt{2}sinx=tgx;
\end{matrix}\right.
\end{matrix}\right.\Leftrightarrow \left[\begin{matrix}
sinx=0, \\\left\{\begin{matrix}
sinx> 0, \\cosx=\displaystyle \frac{\sqrt{2}}{2},
\end{matrix}\right.
\\\left\{\begin{matrix}
sinx< 0, \\cosx=-\displaystyle \frac{\sqrt{2}}{2};
\end{matrix}\right.
\end{matrix}\right. \Leftrightarrow\)
\(\Leftrightarrow \left[\begin{matrix}
x=\pi n, \ n\in z, \\\left\{\begin{matrix}
sinx> 0, \\x=\pm \displaystyle \frac{\pi }{4}+2\pi n, \ n\in z,
\end{matrix}\right.
\\\left\{\begin{matrix}
sinx< 0, \\x=\pm \displaystyle \frac{3\pi }{4}+2\pi n, \ n\in z;
\end{matrix}\right.
\end{matrix}\right. \Leftrightarrow \left[\begin{matrix}
x=\pi n, \ n\in z, \\ x=\displaystyle \frac{\pi }{4}+2\pi n, \ n\in z,
\\x=\displaystyle \frac{5\pi }{4}+\pi n, \ n\in z.
\end{matrix}\right.\)
При отборе решений пользуемся тригонометрическим кругом.
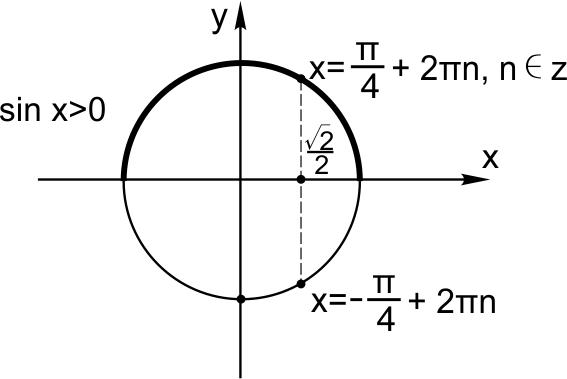
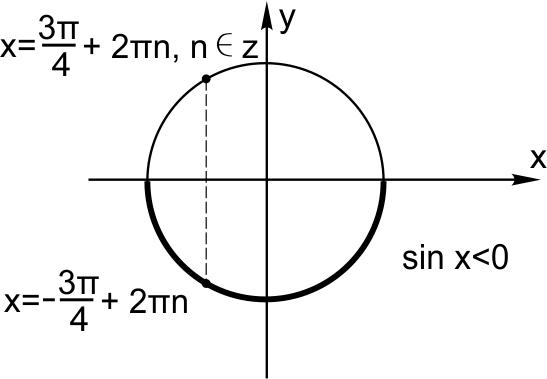
Объединив решения, получим ответ в пункте (а):
\(\pi n, \ n\in Z, \) или \(\displaystyle \frac{\pi}{4}+\pi n, \ n\in Z. \)
В пункте (б) сделаем отбор решений с помощью двойного неравенства.
Дли серии \(\pi n, \ n\in Z: \)
\(-3\pi \leq \pi n \leq 2\pi; \)
\(-3\leq n \leq 2;\)
\(-3\pi, \ -2\pi, \ -\pi, \ 0, \ \pi, \ 2\pi \) – решения.
Для серии \(\displaystyle \frac{\pi}{4}+\pi n, \ n\in Z: \)
\(-3\pi \leq \displaystyle \frac{\pi}{4} +\pi n \leq 2\pi; \)
\(-3 \leq \displaystyle \frac{1}{4} +1 n \leq 2;\)
\(-3\displaystyle \frac{1}{4}\leq n \leq 1\frac{3}{4}.\)
Поскольку \(n\) – целое, \(n= -3, \ -2, \ -1, \ 0\) или \(1\).
Решения на указанном промежутке:
\(-3\pi; \ \displaystyle \frac{-11\pi}{4}; \ -2\pi; \ \displaystyle \frac{-7\pi}{4}; \ -\pi ; \ \displaystyle \frac{-3\pi}{4}; \ 0; \ \displaystyle \frac{\pi}{4}; \ \pi; \ \displaystyle \frac{5\pi}{4}; \ 2\pi.\)
Ответ:
а) \(\pi n, \ n\in Z \) или \(\displaystyle \frac{\pi}{4}+\pi n, \ n\in Z. \)
б) \(-3\pi; \ \displaystyle \frac{-11\pi}{4}; \ -2\pi; \ \displaystyle \frac{-7\pi}{4}; \ -\pi ; \ \displaystyle \frac{-3\pi}{4}; \ 0; \ \displaystyle \frac{\pi}{4}; \ \pi; \ \displaystyle \frac{5\pi}{4}; \ 2\pi.\)






























