Условие задачи
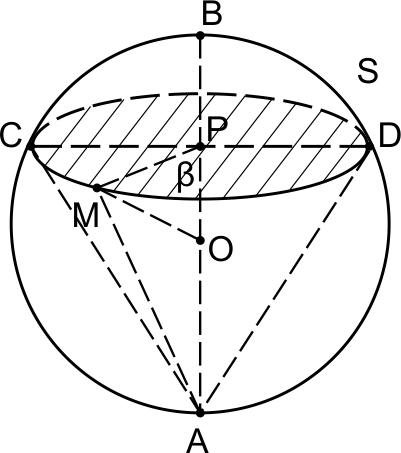
Точка \(P\) лежит на диаметре \(AB\) сферы. При этом \(AP : PB = 3 : 1\). Через прямую \(AB\) проведена плоскость \(\alpha \), а через точку \(P\) – плоскость \(\beta,\) перпендикулярная \(AB\). Отрезок \(CD\) – общая хорда окружностей сечений сферы этими плоскостями, \(S\) – окружность пересечения сферы с плоскостью \(\beta , \ M\) – точка, лежащая на окружности \(S.\)
а) Докажите, что \(AM = CD.\)
б) Найдите объем пирамиды с вершиной \(M\) и основанием \(ABCD\), если диаметр сферы равен 12, а \(M\) – наиболее удаленная от плоскости \(\alpha \) точка окружности \(S.\)
Решение
Поскольку диаметр шара, которым является отрезок \(AB\), лежит в плоскости \(\alpha \), центр шара – точка \(O\) – также лежит в плоскости \(\alpha .\)
Пусть \(P\) – точка пересечения отрезков \(AB\) и \(CD.\) Тогда \(P\in \alpha , \ P\in \beta .\)
\(CD\) – диаметр окружности \(S, \ \alpha \cap \beta =CD.\)
Пусть \(\alpha \) — плоскость чертежа.
Вспомним признак перпендикулярности плоскостей.
Если плоскость \(\alpha \) проходит через перпендикуляр к плоскости \(\beta \), то плоскости \(\alpha \) и \(\beta \) перпендикулярны.
В нашем случае \(\beta \perp AB\) — и значит, \(\beta \perp \alpha .\)
Точка \(M\) лежит на окружности \(S\). Покажем, что \(AM = CD.\)
Треугольники \(APM\) и \(APC\) равны по двум катетам, значит, \(AM=AC.\)
Поскольку точка \(P\) делит отрезок \(AB\) в отношении \(3:1\), а точка \(O\) — середина \(AB\), точка \(P\) является серединой \(OB.\)
\(OP=\displaystyle \frac{1}{2}OB= \frac{1}{2}OC\), так как \(OB\) и \(OC\) — радиусы шара.
В треугольнике \(OPC\) катет \(OP\) вдвое меньше гипотенузы \(OC\), поэтому \(\angle PCO=30^{\circ}, \ \angle POC=60^{\circ}.\)
Тогда \(\angle COD=120^{\circ}=\angle COA=\angle AOD.\)
Равные дуги стягиваются равными хордами, \(AC=CD=AM\) и \(\triangle ACD\) — правильный.
б) Пусть \(M\) — наиболее удалённая от плоскости \(\alpha \) точка окружности \(S.\)
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из точки на плоскость.
Наибольше возможное расстояние от точки \(M\) до плоскости \(\alpha \) будет в случае, если проекцией точки \(M\) на плоскость \(\alpha \) окажется точка \(P.\)
Тогда \(PM\perp \alpha\) и длина отрезка \(PM\) равна радиусу окружности \(S.\)
Найдем \(V_{ACBDM}\) — объем пирамиды с основанием \(ABCD\) и высотой \(PM.\)
Поскольку \(AB \perp CD\) – площадь четырехугольника \(ACBD\), найдем как половину произведения его диагоналей.
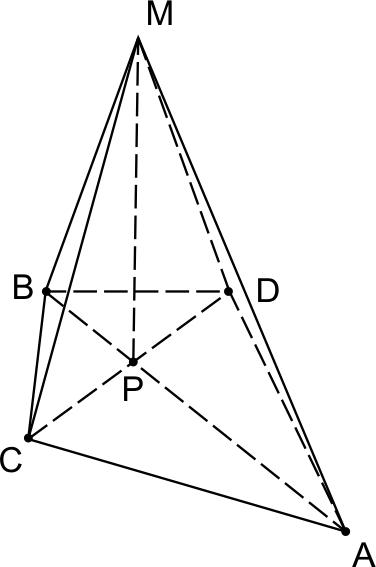
\(S_{ACBD}=\displaystyle \frac{1}{2} AB\cdot CD. \)
\(AP=\displaystyle \frac{1}{2} AB =9, \ BP =\displaystyle \frac{1}{4} AB = 3. \)
По теореме о пересекающихся хордах, \(CP\cdot PD=AP\cdot BP\), отсюда
\(CP=PD=3\sqrt{3}, \ CD= 6\sqrt{3}. \)
\(S_{ACBD}=\displaystyle \frac{1}{2}\cdot 12\cdot 6\sqrt{3}=36\sqrt{3};\)
\(PM = PC = 3\sqrt{3} \) – как радиус окружности \(S.\)
Тогда \(V=\displaystyle \frac{1}{3} S_{ACBD}\cdot PM=\displaystyle \frac{1}{3}\cdot36\sqrt{3}\cdot3\sqrt{3}=108.\)
Ответ:
б) 108.






























