Условие задачи
Авторская задача. Четырехугольник \(ABCD\) вписан в окружность; лучи \(BA\) и \(CD\) пересекаются в точке \(P\), углы \(BPC\) и \(ACD\) равны \(30^{\circ}, \ BC= \sqrt{\displaystyle \frac{3}{2}}AB.\)
а) Докажите, что \(BC\) и \(AD\) параллельны.
б) Найдите длину отрезка, соединяющего середины \(AC\) и \(BD\), если \(R=2\).
Решение
а) Пусть \(O\) – центр окружности, \(R\) – ее радиус.
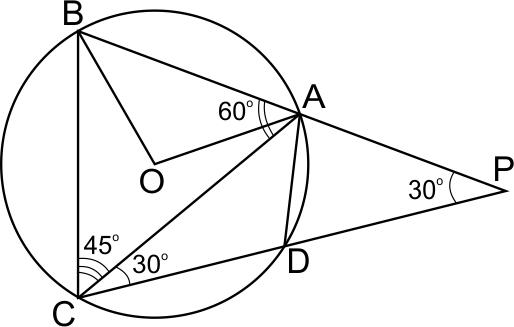
а) Треугольник \(ACP\) – равнобедренный, \(\angle ACP=\angle APC=30^{\circ}\), значит, \(\angle CAP=120^{\circ}, \ \angle BAC=60^{\circ}.\)
\(\angle AOD=60^{\circ}\), так как центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу. Тогда треугольник \(AOD\) – правильный и \(AD=R.\)
По теореме синусов, \(\displaystyle \frac{BC}{sin\angle A}=2R.\) Следовательно, \(\displaystyle \frac{2\cdot BC}{\sqrt{3}}=2R; \ BC=R\sqrt{3}\), тогда \(\sqrt{\displaystyle \frac{3}{2}}AB=R\sqrt{3} \) и \(AB=R\sqrt{2} .\)
Мы получили, что для треугольника \(AOB\) выполняется теорема Пифагора:
\(AB^2=AO^2+OB^2.\)
Значит, \(\angle AOB=90^{\circ}, \ \angle ACB=45^{\circ}\) (как вписанный, опирающийся на ту же дугу).
Из треугольника \(BPC\), где \(\angle P=30^{\circ}, \ \angle C=75^{\circ},\) получим, что \(\angle ABC=180^{\circ}-30^{\circ}-75^{\circ}=75^{\circ} .\)
Значит, \(ABCD\) – равнобокая трапеция и \(AD\parallel BC.\)
б) Докажем, что длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности оснований.
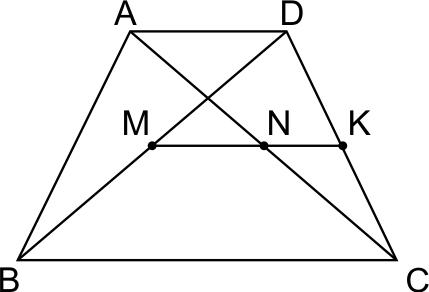
Пусть точка \(M\) – середина диагонали \(BD\) трапеции \(ABCD\). Пусть точка \(K\) – середина стороны \(DC\). Тогда \(MK\) – средняя линия треугольника \(BCD.\)
Пусть \(MK\) пересекает диагональ \(AC\) в точке \(N\). Тогда \(NK\) – средняя линия треугольника \(ADC\), поскольку проходит через середину стороны \(DC\) параллельно \(AD\), то есть \(N\) – середина \(AC.\)
Таким образом, отрезок \(MN\) – это разность средних линий треугольников \(BDC\) и \(ADC\), и его длина равна полуразности оснований.
\(MN=\displaystyle \frac{BC-AD}{2}=\displaystyle \frac{R(\sqrt{3}-1)}{2}.\)
Если \(R=2,\) то \(MN=\sqrt{3}-1.\)
Ответ:
\(MN=\sqrt{3}-1.\)






























