Условие задачи
Найдите все значения, при каждом из которых наименьшее значение функции \(f(x)=4ax+|x^2-6x+5| \) больше, чем -24.
Решение
Чего не стоит делать в этой задаче? Не стоит строить график функции \(f(x)=4ax+|x^2-6x+5| \). Вместо этого сформулируем условие задачи немного по-другому.
Нам надо найти такие значения \(a\), чтобы наименьшее значение функции \(f(x)\) было больше, чем - 24. Это значит, что все значения функции \(f(x)\) будут больше -24. Другими словами, мы ищем такие значения параметра \(a\), чтобы неравенство
\(4ax + |x^2- 6x + 5| > - 24 \) выполнялось для любого \(x\).
Запишем неравенство в виде:
\( |x^2- 6x + 5| > - 4ax- 24.\)
Обозначим \(b = -4a:\)
\(|x^2- 6x + 5| > bx- 24. \)
Решим это неравенство графически. График правой части – прямая с угловым коэффициентом \(b\), проходящая через точку \((0; -24).\)
График левой части построить легко. Мы строим квадратичную параболу \(y= x^2- 6x + 5\).
Эта функция равна нулю при \(x = 1\) и \(x = 5\), вершина параболы в точке с координатами \((3; -4)\). Затем отражаем вверх часть параболы, лежащую ниже оси \(X.\)
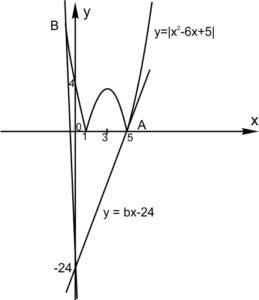
Выполнение неравенства \(| x^2- 6x + 5|> bx- 24 \) для всех \(x\) означает, что весь график функции \(y= | x^2- 6x + 5 |\) лежит выше прямой \(у= bх- 24\). Найдем, при каких значениях углового коэффициента \(b\) это происходит.
В точках \(A\) и \(B\) прямая \(y= bx- 24\) касается графика функции \(y= | x^2- 6x + 5 |\). Поскольку точки \(A\) и \(B\) лежат выше оси \(X\), их ординаты положительны и в формуле функции
\(y= | x^2- 6x + 5 |\) модуль раскрывается с «плюсом».
Запишем условия касания:
\(\left\{\begin{matrix} x^2-6x+5=bx-24,\\ 2x-6=b.\end{matrix}\right. \)
Подставив \(b = 2x – 6\) в первое уравнение, получим: \(x^2 = 29\). Абсциссы точек \(A\) и \(B\) – это \(\sqrt{29}\) и \(-\sqrt{29}\).
В точке \(A: \ b = 2 \sqrt{29} -6, \)
В точке \(B: \ b = - 2 \sqrt{29} -6. \)
Неравенство \(| x^2- 6x + 5|> bx- 24 \) выполняется, если \(- 2 \sqrt{29} -6 < b < 2 \sqrt{29} -6. \)
Поскольку \(b = -4a\), для \(a\) получим условие: \(a\in \left(\displaystyle \frac{3-\sqrt{29}}{2};\frac{3+\sqrt{29}}{2}\right).\) Это ответ.














































