Условие задачи
Найдите все значения параметра \(a\), при каждом из которых неравенство
\(|(|x^2-6x+5|-x^2+6x-13)|< a-a^2-(x-2)^2+2x-4\) имеет единственное целое решение.
Решение
Преобразуем зависящее от \(x\) выражение в правой части неравенства, раскрыв скобки:
\(-(x-2)^2+2x-4=-x^2+4x-4+2x-4=-x^2+6x-8=-(x^2-6x+8).\)
Сделаем замену: \(z=x^2-6x+5.\)
Тогда \(-x^2+6x-13=-(x^2-6x+13)=-(z+8).\)
Неравенство примет вид: \(|(|z|-z-8)|+z<a-a^2-3.\)
Обозначим \(a-a^2-3=b. \)
\(|(|z|-z-8)|+z<b.\)
Оценим, какие значения может принимать \(z=x^2-6x+5.\) Выделим полный квадрат:
\(z=x^2-6x+5=x^2-6x+9-4=(x-3)^2-4\geq -4.\)
Заметим, что если \(x\) – целое, то \(z(x)\) – тоже целое.
Построим график функции \(y(z)=|(|z|-z-8)|+z\) при \(z\geq -4.\)
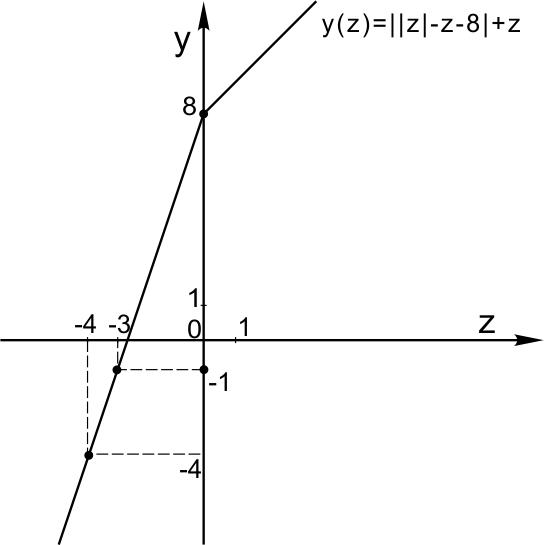
\(y(z)=z+8 ,\) если \(z\geq 0; \)
\(y(z)=3z+8,\) если \(z<0.\)
Функция \(y(z)\) монотонно возрастает, то есть каждое свое значение принимает ровно один раз.
Если \(b\in(-4; -1] \), неравенство \( y(z) < b\) имеет единственное целое решение \(z=-4 \).
Если \(b \leq -4\) – решений нет.
Если \(b > -1\) - неравенство имеет более одного целого решения \(z\).
Если \( z=z_0 \) – решение неравенства, то все \(z<z_0\) также будут решениями неравенства.
Мы получили, что если \(b\in(-4; -1] \), то неравенство \(|(|z|-z-8)|+z < b \) имеет единственное целое решение \(z=-4 \).
Если \(z=(x-3)^2-4=-4\), то \(x=3\), и значит, исходное неравенство также имеет единственное целое решение \(x=3.\)
Найдем, при каких \(a\) это произойдет.
\(\left\{\begin{matrix}
a-a^{2}-3\leq -1, \\a-a^{2}-3> 4;
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
a^{2}-a+2\geq 0 - верно \ всегда, \\a^{2}-a-1< 0; \end{matrix}\right.\Leftrightarrow a^{2}-a-1< 0, \ a\in \left (\displaystyle \frac{1-\sqrt{5}}{2};\displaystyle \frac{1+\sqrt{5}}{2}\right).\)
Ответ:
\(a\in \left (\displaystyle \frac{1-\sqrt{5}}{2};\displaystyle \frac{1+\sqrt{5}}{2}\right).\)






























