Условие задачи
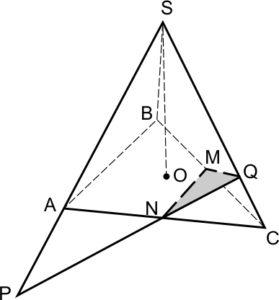
(Авторская задача) На продолжении ребра \(SA\) правильного тетраэдра \(SABC\) отмечена точка \(P\) так, что \(SA = 2 AP\). Точки \(M\) и \(N\) – середины ребер \(BC\) и \(AC\) соответственно. Прямая \(PN\) пересекает ребро \(SC\) в точке \(Q\).
а) Докажите, что плоскость \(QMN\) перпендикулярна ребру \(SC\).
б) Найдите объем треугольной пирамиды \(SQMN\), если все ребра тетраэдра равны 4.
Решение
а) Покажем, что \((MNQ) \perp SC.\)
Правильный тетраэдр – треугольная пирамида, все грани которой представляют собой правильные треугольники. Скрещивающиеся ребра правильного тетраэдра взаимно перпендикулярны, поэтому \(AB\perp SC\). Это легко доказать.
Отрезок \(CO\) – проекция ребра \(SC\) на плоскость основания.
\(CO\perp AB,\) так как \(O\) – центр правильного треугольника \(ABC\). По теореме о трех перпендикулярах \(SC\perp AB.\) Заметим, что \(MN\parallel AB\) как средняя линия в треугольнике \(ABC\), и значит, \(SC\perp MN.\)
Пусть ребро тетраэдра равно \(a.\)
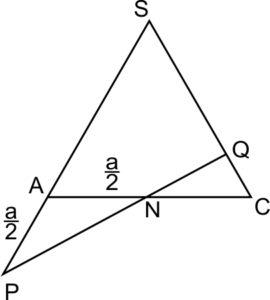
Отрезок \(PQ\) лежит в плоскости боковой грани \(SAC.\)
Треугольник \(APN\) – равнобедренный, \(AP=AN=\displaystyle \frac{a}{2}\); тогда
\(\angle APN=\angle ANP=\displaystyle\frac{180^{\circ}-\angle PAN}{2}=\displaystyle\frac{180^{\circ}-120^{\circ}}{2}=30^{\circ}. \)
\(\angle NCQ=60^{\circ},\) тогда из \(\triangle NCQ\) получим, что \(\angle NQC=90^{\circ}, \; PQ\perp SC.\)
Таким образом, прямая \(SC\) перпендикулярна двум пересекающимся прямым \(MN\) и \(NQ\), лежащим в плоскости \(MNQ\). Значит, она перпендикулярна и всей плоскости \(MNQ.\)
б) Найдем объем пирамиды \(SMNQ.\)
Пусть \(\triangle MNQ\) – основание пирамиды, \(SQ\) – ее высота, поскольку \(SQ\perp (MNQ).\)
В треугольнике \(CNQ\) угол \(QNC\) равен \(30^{\circ}\), следовательно,
\(QC=\displaystyle\frac{1}{2}; \; NC=\frac{1}{4}; \; AC=1, \; SQ=\frac{3}{4}; \; AC=3; \; NQ=\sqrt{3}.\)
Поскольку треугольники \(NCQ\) и \(MCQ\) равны, \(MQ=NQ=\sqrt{3}.\)
В треугольнике \(NMQ: \; MQ=NQ=\sqrt{3}; \; MN=\displaystyle\frac{1}{2} AB=2;\)
\(S_{ \Delta NMQ}=\sqrt{2}; \; V_{ SNMQ}=\displaystyle \frac{1}{3}\cdot 3\cdot \sqrt{2}=\sqrt{2}.\)
Ответ:
б) \( V_{ SNMQ}=\sqrt{2}.\)