Условие задачи
Найдите все значения параметра \(a\), при каждом из которых система уравнений
\(\left\{\begin{matrix}
\displaystyle \frac{xy^{2}-3xy-3y+9}{\sqrt{x+3}}=0, \\
y=ax
\end{matrix}\right. \; \) имеет ровно два различных решения.
Решение
Разложим на множители числитель дроби в первом уравнении:
\(xy^2-3xy-3y+9=xy(y-3)-3(y-3)=(xy-3)(y-3).\)
Система примет вид:
\(\left\{\begin{matrix}
\displaystyle \frac{(xy-3)(y-3)}{\sqrt{x+3}}=0,\\
y=ax.
\end{matrix}\right. \)
Область допустимых значений: \(x>-3.\)
\(\left\{\begin{matrix}
\left[\begin{matrix}
xy-3=0, \\y=3,
\end{matrix}\right. \\x> -3,
\\y=ax;
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
\left[\begin{matrix}
y=\displaystyle \frac{3}{x}, \\y=3,
\end{matrix}\right. \\x> -3,
\\y=ax.
\end{matrix}\right. \)
Решим систему графически:
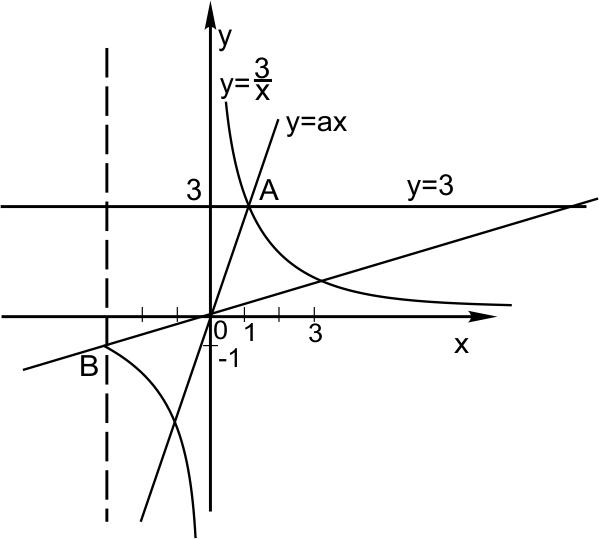
Система имеет ровно 2 различных решения только в следующих случаях:
1) Прямая \(y=ax\) проходит через точку \(A(1;3).\) Тогда \(a=3.\)
2) Прямая \(y=ax\) пересекает только правую ветвь гиперболы \(y=\displaystyle \frac{3}{x}\) и прямую \(y=3\).
Это значит, что точка пересечения прямых \(y=ax\) и \(x=-3\) лежит выше точки \(B\) и ниже оси абсцисс.
В точке \(B (-3;1)\) значение параметра \(a\) равно \(\displaystyle \frac{1}{3}.\)
Значит, ровно два решения в этом случае будут, если \(0 < a < \displaystyle \frac{1}{3}.\)
Ответ:
\(\left (0; \displaystyle \frac{1}{3}\right )\cup \begin{Bmatrix}
{3}
\end{Bmatrix}.\)




























