Условие задачи
Площадь полной поверхности конуса равна 9, образующая наклонена к основанию под углом 60°. Найти площадь поверхности сферы, вписанной в конус.
Решение
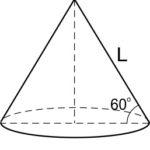
Осевое сечение конуса – правильный треугольник.
Если \(R\) – радиус основания, \(L\) – образующая, то \(L=2R.\)
Площадь полной поверхности конуса:
\(S_{полн}=\pi R^2+\pi RL=\pi R^2+2\pi R^2=3\pi R^2=9,\) тогда \(R=\sqrt{\displaystyle \frac{3}{\pi }}\) и \( L=2\cdot \sqrt{\displaystyle \frac{3}{\pi }}.\)
Радиус окружности, вписанной в правильный треугольник со стороной \( L=2\cdot \sqrt{\displaystyle \frac{3}{\pi }}\), равен \(L\cdot \displaystyle \frac{\sqrt{3}}{6}=\displaystyle \frac{1}{\sqrt{\pi }},\) а площадь сферы с таким радиусом равна \(4\pi r^2=4.\)
Ответ:
4.






























