Условие задачи
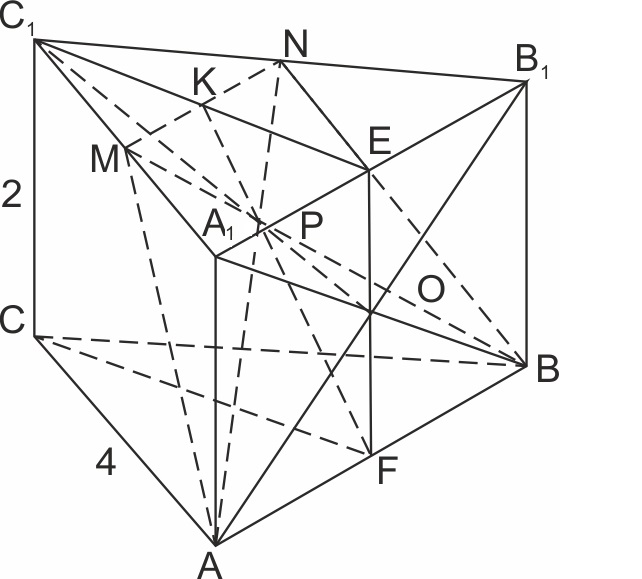
(ЕГЭ-2019) В правильной треугольной призме \(ABCA_1B_1C_1\) сторона основания равна 4, а боковое ребро равно 2. Точка M — середина ребра \(A_1C_1,\) а точка O — точка пересечения диагоналей боковой грани \(ABB_1A_1.\)
а) Докажите, что точка пересечения диагоналей четырёхугольника, являющегося сечением призмы \(ABCA_1B_1C_1\) плоскостью AMB лежит на отрезке \(OC_1.\)
б) Найдите угол между прямой \(OC_1,\) и плоскостью AMB.
Решение
а) Сечение — равнобедренная трапеция AMNB, причём MN - средняя линия \(\displaystyle \triangle A_1B_1C_1; MN = \frac{1}{2}AB.\)
Пусть E — середина \(A_1B_1, F\) — середина AB, K — середина MN
\(P=AN \cap NM\) (точка пересечения диагоналей трапеции AMNB).
\(P \in KF\) (замечательное свойство трапеции);
\(\displaystyle \triangle KPN \sim \triangle FPB, \, \frac{KP}{PF} = \frac{KN}{FB} = \frac{1}{2}.\)
Покажем, что \(P = KF \cap OC_1.\)
Построим сечение призмы плоскостью \(C_1EF.\)
\(FP:PK = 2:1,\) FK - медиана \(\triangle FC_1E,\) значит, P - точка пересечения медиан \(\triangle FC_1E; C_1O\) - медиана, тогда \(FK \cap C_1O = P.\)
Найдём угол между \(OC_1 \)и \(AMB.\) Проведём \(OH \perp FK; \, \, OH \in (CC_1E).\)
Кроме того, \(OF \perp AB,\) т.к. \(OH \in (CC_1E); \, \, (CC_1E) \perp AB.\)
Значит, \(OH \perp (AMB);\) FK — проекция \(OC_1\) на \((AMB), \, \varphi = \angle FPO\) — искомый. Найдём \(\angle CPF\) — смежный с \(\angle \varphi.\)
Из \(\triangle C_1PF\) найдём по теореме косинусов \(cos \angle C_1PF. \)
\(CF = 2\sqrt{3}\) (высота правильного \( \triangle ABC)\)
\(\displaystyle C_1P = \frac{2}{3}. C_1O = \frac{2}{3}\sqrt{13}; FP = \frac{2}{3}\sqrt{7}, C_1F = 4; cos \varphi = \frac{8}{\sqrt{91}}\)
Ответ
\(\displaystyle \varphi = arccos \frac{8}{\sqrt{91}}\)