Условие задачи
Дмитрий Мухин
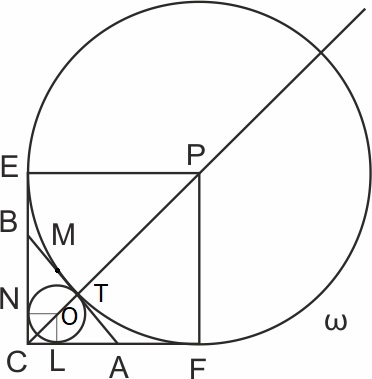
B прямоугольном треугольнике ABC угол C - прямой. Точка O - центр вписанной окружности, точка P - центр окружности \(\omega,\) касающейся гипотенузы AB и продолжений катетов CB и CA.
а) докажите, что \(OP=\sqrt{2}AB.\)
б) найдите радиус \(\omega,\) если радиус вписанной окружности равен 1, а длина отрезка AB равна 6
Решение
а) Докажем, что \(OP = \sqrt2 AB.\)
Центр окружности, вписанной в угол, лежит на биссектрисе угла.
Пусть \(\omega\) - вневписанная окружность, \(\omega\) - вписанная в \(\triangle ABC\)
Тогда CP - биссектриса угла C, \(O \in CP.\)
Проведём перпендикуляры
\(PE \perp (BC), \, \, ON \perp (BC),\)
\(PF \perp (AC), \, \, OL \perp (AC).\)
ONCL- квадрат, т.к. \(LC = \angle L = \angle N = 90^\circ.\)
Аналогично, PFCE - квадрат,
PE = PF = R.
Для окружности, вписанной в прямоугольный треугольник:
\(\displaystyle r = \frac{a+b+c}{2}.\)
Докажем, что \(OL = ON = CN = CL = r.\) Пусть \(AC = b, \, BC=a.\)
Тогда \(AL = b - r, \, BN = a - r.\)
Пусть T - точка касания
\(AT = AL = b - r, \, BT = BN = a -r;\)
\(AT + BT = AB = a -r +b -r =c,\) отсюда \(\displaystyle c = \frac{a+b-c}{2}.\)
Аналогично, найдём радиус окружности \(\omega.\)
Пусть M - точка касания \(\omega\) и \(AB;\)
PFCE - квадрат, \(CE = a+BE=R;\)
\(CF = b + AF = R;\)
\(CE + CF = a+ b+BE+AF=2R;\)
\(BM = BE; \, AF = AM; \, a + b + c = 2R,\) отсюда
\(\displaystyle R = \frac{a+b+c}{2}.\)
Далее, \(CP = R\sqrt{2}, \, CO = r \sqrt2,\)
\(\displaystyle OP = CP - CO = (R-r) \cdot \sqrt2 = \sqrt2 (\frac{a+b+c}{2}-\frac{a+b-c}{2}) = c\sqrt2\)
б) Найдём \(\omega,\) если \(r=1, \, AB = c = 6.\)
\(OP = 6\sqrt2; \, OC = \sqrt2, \, CP = OP+OC = 7 \sqrt2,\)
\(\displaystyle R = \frac{CP}{\sqrt2} = 7\)
Ответ
7