Условие задачи
а) Решите уравнение: \(2sin^2x+\sqrt{2}sin\left (x+\displaystyle \frac{\pi }{4}\right )=cosx.\)
б) Укажите корни этого уравнения, принадлежащие отрезку \(\left [-2\pi; -\displaystyle \frac{\pi }{2} \right ].\)
Решение
a) По формуле синуса суммы, \( sin\left (x+\displaystyle \frac{\pi }{4}\right ) =\displaystyle \frac{\sqrt{2}}{2} sin x+\frac{\sqrt{2}}{2} cos x.\)
Уравнение примет вид: \(2sin^2x+sinx+cosx=cosx \Leftrightarrow 2sin^2x+sinx=0 \Leftrightarrow sinx(2sinx+1)=0 \Leftrightarrow \)
\(\Leftrightarrow \left[
\begin{gathered}
sinx=0, \\
sinx=-\frac{1}{2}; \\
\end{gathered}
\right. \Leftrightarrow \left[
\begin{gathered}
x=\pi n, \ n\in z, \\
x=-\frac{\pi}{6} +2\pi n,\\
x=-\frac{5\pi}{6} +2\pi n.\\
\end{gathered}\right.
\)
б) Отберём корни, принадлежащие отрезку \(\left [-2\pi; -\displaystyle \frac{\pi }{2} \right]\), с помощью тригонометрического круга:
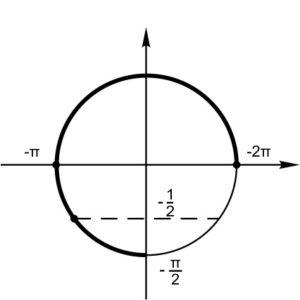
Указанному отрезку принадлежат числа \(-2\pi; \ -\pi; \ -\displaystyle \frac{5\pi}{6}.\)
Ответ:
а) \(\left[
\begin{gathered}
x=\pi n,\ n\in z; \\
x=-\displaystyle \frac{\pi}{6} +2\pi n,\\
x=-\displaystyle \frac{5\pi}{6} +2\pi n.\\
\end{gathered}\right.\)
б) \(-2\pi; \ -\pi;\ -\displaystyle \frac{5\pi}{6}\).














































