Условие задачи
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка \( C_1 \), причём \(CC_1\) — образующая цилиндра, а AC — диаметр основания. Известно, что \(\angle ACB=30^{\circ},~AB=\sqrt{2},~ CC_1=2.\)
а)Докажите, что угол между прямыми \(AC_1\) и \(BC\) равен \(45^{\circ}\).
б)Найдите объём цилиндра.
Решение
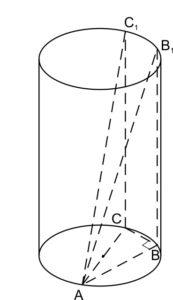
Прямые \(BC\) и \(B_1C_1\) параллельны, (как линии пересечения двух параллельных оснований цилиндра третьей плоскостью).
Значит, угол между \(AC_1\) и \(BC\) равен углу \(AC_1B_1.\)
\( \angle ABC=90^{\circ}\) (опирается на диаметр).
Из \(\Delta ABC: \)
\(BC=AB\cdot \sqrt{3}=\sqrt{6}=B_1C_1; \ AC=2\sqrt{2}. \)
Из \(\Delta ACC_1: \)
\(AC_1=\sqrt{AC^2+CC_1^2}=\sqrt{8+4}=\sqrt{12}=2\sqrt{3}. \)
Из \(\Delta ABB_1: \)
\(AB_1=\sqrt{AB^2+BB_1^2}=\sqrt{2+4}=\sqrt{6}=B_1C_1. \)
Для \(\Delta AC_1B_1 \) выполняется равенство \( AC_1^2=B_1C_1^2+AB_1^2; \ 6+6=12.\)
Значит, \(\Delta AC_1B_1 \) — прямоугольный равнобедренный, \(\angle AC_1B_1 =45^{\circ}.\)
б) Найдем \(V\) цилиндра: \( V=\pi R^2\cdot h=\pi \cdot (\sqrt{2})^2 \cdot 2 =4\pi.\)


























