Условие задачи
Решите неравенство: \(log_5(3x+1)+log_5\left (\displaystyle \frac{1}{72x^2}+1\right )\geq log_5\left (\displaystyle \frac{1}{24x}+1\right ). \)
Решение
\(log_5(3x+1)+log_5\left (\displaystyle \frac{1}{72x^2}+1\right )\geq log_5\left (\displaystyle \frac{1}{24x}+1\right ) \Leftrightarrow \)
\(\Leftrightarrow \left\{\begin{matrix} 3x+1>0,\\ \displaystyle \frac{1}{72x^2}+1>0,\\
\displaystyle \frac{1}{24x}+1>0,\\ log_5\left ((3x+1)\cdot\left (\displaystyle \frac{1}{72x^2}\right )\right )+1\geq log_5\left (\displaystyle \frac{1}{24x}+1\right );
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
x>\displaystyle \frac{1}{3},\\ x\neq 0,\\ \displaystyle \frac{24x+1}{x}>0,\\
(3x+1)\cdot\left (\displaystyle \frac{1}{72x^2}+1\right )\geq \displaystyle \frac{1}{24x}+1.
\end{matrix}\right.\)
ОДЗ неравенства: \(\left[\begin{gathered} -\frac{1}{3}<x<-\frac{1}{24},\\ x>0. \end{gathered} \right.\)
Раскроем скобки в последнем неравенстве системы:
\(\displaystyle \frac{1}{24x}+\displaystyle \frac{1}{72x^2}+3x+1\geq \displaystyle \frac{1}{24x}+1;\)
\(\displaystyle \frac{1}{72x^2}+3x \geq 0;\)
\(\displaystyle \frac{1+216x^3}{72x^2}\geq 0.\)
При \(x\neq 0\) получим: \(1+216x^3 \geq 0;\)
\(216x^3 \geq -1;\)
\((6x)^3 \geq (-1)^3;\)
\(6x \geq -1;\)
\(x \geq \displaystyle -\frac{1}{6}.\)
С учетом ОДЗ:
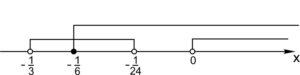
Ответ: \(x\in \left [-\displaystyle \frac{1}{6};-\frac{1}{24}\right )\cup (0; +\infty).\)






























