Условие задачи
Четырёхугольник \(ABCD\) вписан в окружность радиуса \(R=8.\) Известно, что \(AB=BC=CD=12.\)
а) Докажите, что прямые \(BC\) и \(AD\) параллельны.
б) Найдите \(AD.\)
Решение
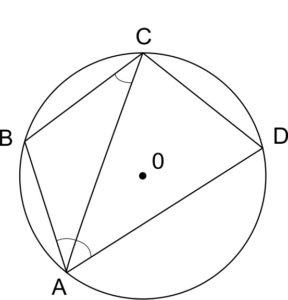
а) Докажем, что \(BC\parallel AD.\)
Равные дуги стягиваются равными хордами.
Дуги \(AB\) и \(CD\), стягиваемые равными хордами \(AB\) и \(CD\), равны.
Значит, \(\angle ACB=\angle CAD\) — как опирающиеся на равные дуги. Эти углы — накрестлежащие при прямых \(BC\) и \(AD\) и секущей \(AC.\)
Значит, \(AD\parallel BC.\)
б) Найдем \(AD\), если \(AB=BC=CD=12, \ R=8.\)
По теореме синусов, \(\displaystyle \frac{AB}{sin\angle ACB}=2R;\)
\(\displaystyle \frac{AB}{2R}=sin\angle ACB\), отсюда \(sin\angle ACB=\displaystyle \frac{3}{4}.\)
\(\angle BAC=\angle CAD=\angle BCA= \varphi\) — так как опираются на равные хорды.
Так как \(ABCD\) — равнобедренная трапеция, \(\angle CDA=2\cdot \angle BCA =2\varphi;\)
\(sin\angle CDA=sin 2\varphi = 2sin\varphi cos\varphi.\)
По теореме синусов из треугольника \(CDA:\)
\(\displaystyle \frac{AC}{sin\angle CDA}=\frac{CD}{sin\angle CAD};\)
\(\displaystyle \frac{AC}{2sin\varphi cos\varphi }=\frac{CD}{sin\varphi};\)
\(AC=CD\cdot 2cos\varphi =24 cos\varphi. \)
По теореме косинусов из \(\triangle ACD:\)
\(CD^2=AC^2+AD^2-2AC\cdot AD\cdot cos \angle ACD;\)
\(12^2=(24cos\varphi )^2+AD^2-2\cdot 24\cdot AD \cdot cos^2 \varphi. \)
\(sin \varphi =\displaystyle \frac{3}{4} \Rightarrow cos^2 \varphi =1-\frac{9}{16}=\frac{7}{16}.\)
Обозначим \(AD=x.\)
\(12^2=24^2\cdot \displaystyle \frac{7}{16}+x^2-2\cdot 24 \cdot x \cdot \frac{7}{16};\)
\(x^2-21x+108=0;\)
\(x=12\) или \(x =9.\)
Если \(x=12,\) то \(ABCD\) — квадрат (ромб, вписанный в окружность). Тогда условие \(R=8\) не выполняется.
Ответ: \(AD=9.\)






























