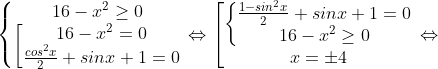Видеоразбор: https://www.youtube.com/watch?v=q2a7-1HK9dk\&t=1s и https://www.youtube.com/watch?v=oTbmPJy8v0I\&t=6703s
Часть 1. Задания с кратким ответом
1. Анна Малкова
Четырехугольник ABCD с равными углами BCD и DAB вписан в окружность, AB = 14, AD = 48, CD = 40. Найдите BC.
Решение:
Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны \(180 ^\circ .\)
ABCD - вписан в окружность \(\Rightarrow \) \(\angle A+\angle C=\angle B+\angle D=180 ^\circ \)
Тогда \(\angle BCD=\angle DAB=90 ^\circ .\) Это значит, что \(BD\ \) – диаметр окружности.
Из \(\triangle ABD\) по теореме Пифагора:
\({BD}^2={AB}^2+{AD}^2;\ {BD}^2={14}^2+{48}^2=50^2\)
Из \(\triangle BCD:\ \ {BC}^2={BD}^2-{CD}^2;\ \)
\({BC}^2={50}^2-{40}^2=900\ \Rightarrow \ BC=30.\)
Ответ: 30
2. Анна Малкова
Снеговик собран из трех снежных шаров, поставленных друг на друга, причем их радиусы относятся как 5 : 3 : 2, а высота снеговика равна 1,5 метра. Найдите массу снеговика (в кг). Шары считать идеальными, число \(\pi \) принять равным 3,14, плотность снега - равной 400 кг/м³. Ответ округлить до целого числа килограммов, объемом морковки пренебречь.
Решение:
Запишем диаметры шаров как обыкновенные дроби:
\(\displaystyle D_1=0,5\ \cdot 1,5=0,75=\frac{3}{4};\)
\(\displaystyle D_2=0,3\cdot 1,5=0,45=\frac{45}{100}=\frac{9}{20};\)
\(\displaystyle D_3=0,2\cdot 1,5=0,3=\frac{3}{10}.\)
Применим формулу объема шара: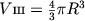 
и сложим объемы трех шаров, из которых собран снеговик.
\(\displaystyle V=\frac{4}{3}\cdot \frac{\pi }{8}\left ({\left (\frac{3}{4}\right ) }^3+{\left (\frac{9}{20}\right ) }^3+{\left (\frac{3}{10}\right ) }^3 \right )=\frac{\pi }{8\cdot 6}\left({\left (\frac{3}{2}\right ) }^3+{\left ( \frac{9}{10}\right )}^3+{\left ( \frac{3}{5}\right )}^3\right )=\)
\(\displaystyle =\frac{\pi }{48}\cdot \left ({\left (\frac{15}{10}\right )}^3+{\left (\frac{9}{10}\right )}^3+{\left (\frac{6}{10}\right )}^3\right )=\frac{\pi }{48}\cdot \frac{1}{1000}\cdot \left ({15}^3+9^3+6^3\right )=\)
\(\displaystyle =\frac{\pi \cdot 3^3}{48\cdot 1000}\cdot (125+27+8)=\frac{\pi \cdot 9}{16\cdot 1000}\cdot (125+27+8)=\)
\(\displaystyle =\frac{\pi \cdot 9}{1000\cdot 16}\cdot 160=\frac{\pi \cdot 9}{100}\)
\(\displaystyle m=\frac{3,14\cdot 9\cdot 400}{100}=3,14\cdot 36=113,04\approx 113\) кг.
Ответ: 113
3. Александра Антонова
В шкафу Деда Мороза вперемешку лежат все его 9 шапок, а также случайно оказавшаяся там шапочка Снегурочки. 31 декабря Дед Мороз, опаздывая на детский утренник, наугад надевает первую попавшуюся шапку. Найдите вероятность того, что он возьмет не свою шапку.
Решение: согласно определению вероятности, она равна отношению числа благоприятных исходов к общему число исходов. Благоприятный исход один из десяти возможных, значит, р = 0,1.
Ответ: 0,1
4. Татьяна Сиротина
У Пятачка есть три воздушных шарика: синий, зеленый и желтый.
Винни-Пух просит у него синий шарик и за это обещает угостить мёдом. Ослик Иа хочет зеленый и за это обещает спеть песенку, причем шарики других цветов Пуху и Ослику не подойдут. Кролик готов сказать «спасибо» за шарик любого цвета.
Известно, что Винни-Пух с вероятностью 0,7 сам съест весь мёд, а ослик Иа с вероятностью 0,4 не захочет петь, получив шарик. Пятачок отправил по почте каждому из друзей по шарику, но при этом забыл, кому какого цвета нужен шарик. Найдите вероятность, того, что все друзья Пятачка выполнят свои обещания.
Решение:
Кролик скажет Пятачку «спасибо» в любом случае. Остаются Винни-Пух и Иа. Винни-Пух хочет синий шарик, а ослик Иа – зеленый. Пятачок забыл, кому какой шарик нужен, поэтому возможных исходов всего 6. Покажем их, обозначив зеленый, синий и желтый шарики буквами З, С и Ж.
| Ослик Иа | Винни Пух | Кролик |
| З | С | Ж |
| З | Ж | С |
| Ж | З | С |
| Ж | С | З |
| С | Ж | З |
| С | З | Ж |
Благоприятный исход только один (первый в таблице). Вероятность того, что друзья Пятачка получат шарики нужного цвета, равна \(\displaystyle \frac{1}{6}.\)
Правда, Винни-Пух сам съест весь мёд с вероятностью 0,7 (а не съест с вероятностью 1 – 0,7 = 0,3). Ослик Иа после получения зеленого шарика захочет спеть с вероятностью 1 – 0,4 = 0,6. Значит, вероятность того, что друзья Пятачка получат шарики нужного цвета, и при этом Винни Пух угостит Пятачка мёдом, а ослик Иа споет песню (независимые события) равна \(\displaystyle =\frac{1}{6}\cdot 0,3 \cdot 0,6 = 0,03.\)
Ответ: 0,03.
5. Анна Малкова
Решите уравнение: \({\pi }^{{cos \pi x\ }}\)=1.
В ответе запишите наибольший отрицательный корень.
Решение:
\(\displaystyle \pi ^{{cos \pi x\ }}=1\Leftrightarrow \pi ^{{cos \pi x\ }}=\pi ^0 \Leftrightarrow {cos \pi x\ }=0\Leftrightarrow \pi x=\frac{\pi }{2}+\pi k,\ \ k\in Z\)
\(\displaystyle x=\frac{1}{2}+k,\ k\in Z\)
\(k=-1\Rightarrow x=-0,5\)
Ответ: -0,5
6. Анна Малкова
Вычислите: \(\displaystyle \frac{{sin (\frac{\pi }{2}+x)\ }+\sqrt{1-{{sin}^2 x\ }}}{{sin}^2x+{{cos}^3(\pi - x\ })+ctg(x+\ \frac{3\pi }{2})}\ \ \ \)при \(x\in (\frac{\pi }{2};\pi ).\)
Решение:
\(\displaystyle \frac{{sin (\frac{\pi }{2}+x)\ }+\sqrt{1-{{sin}^2 x\ }}}{{{sin}^2 x\ }+{{cos}^3 (\pi -x)\ }+ctg(x+\frac{3\pi }{2})}=\frac{{cos x\ }+\left|{cos x\ }\right|}{{{sin}^2 x\ }-{{cos}^3 x-tgx\ }}=\)
\(\displaystyle =\frac{{cos x\ }-{cos x\ }}{{{sin}^2 x\ }-{{cos}^3 x-tgx\ }}=0\)
Не будет ли знаменатель равен нулю?
- Нет, не будет.
при \(\displaystyle x\in (\frac{\pi }{2};\pi )\) имеем:
\({{sin}^2 x> 0; \; {cos x< 0; \; tg\ x< 0,\ \ }\ }\) тогда \({{sin}^2 x\ }-{{cos}^3 x-tgx\ }\textgreater 0.\ \) Ответ: 0 7. Анна Малкова
На рисунке изображена часть графика производной функции \(y=f(x).\) В какой точке отрезка [-4; 5] функция \(y=f(x)\) принимает наибольшее значение?
Решение:
Так как \(f'(x)\textless 0\) при \(x\in [ -4;5]\) , то \(f(x)\) - монотонно убывает при \(x\in [ -4;5],\) поэтому наибольшее значение функция достигает в левом конце этого отрезка, то есть при \(x=-4.\)
Ответ: -4
8. ФИПИ
Груз массой 0,25 кг колеблется на пружине со скоростью, меняющейся по закону \(v(t)=1,6{cos \pi t\ },\) где \(t\)– время в секундах. Кинетическая энергия груза вычисляется по формуле \(\displaystyle E=\frac{mv^2}{2},\) где \(m\) – масса груза (в кг), \(v\) – скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее \(2,4\cdot {10}^{-1}\) Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Решение:
\(v(t)=1,6{cos \pi t\ };\)
\(\displaystyle E=\frac{mv^2}{2};\)
\(E_k\ge 2,4\cdot {10}^{-1}\) Дж.
Получим:
\(\displaystyle \frac{0,25\cdot {1,6}^2\cdot {{cos}^2 \pi t\ }}{2}\ge 2,4\cdot {10}^{-1}\Leftrightarrow \frac{25\cdot {1,6}^2\cdot {{cos}^2 \pi t\ }}{2}\ge 24\Leftrightarrow \)
\(\displaystyle \Leftrightarrow {1,6}^2\cdot {{cos}^2 \pi t\ }\ge \frac{48}{25}\Leftrightarrow \frac{256}{100}\cdot {{cos}^2 \pi t\ }\ge \frac{48\cdot 4}{100}\Leftrightarrow \)
\(\displaystyle \Leftrightarrow 16\cdot {{cos}^2 \pi t\ }\ge 12\Leftrightarrow {{cos}^2 \pi t\ }\ge \frac{3}{4}.\)
Воспользуемся формулой понижения степени. По формуле косинуса двойного угла, \({cos 2x=2{{cos}^2 x\ }-1\ },\) отсюда \(\displaystyle {{cos}^2 x\ }=\frac{{cos 2x\ }+1}{2}\)
\(\displaystyle {{cos}^2 \pi t\ }=\frac{{cos 2\pi t\ }+1}{2}. \)
\(\displaystyle \frac{{cos 2\pi t\ }+1}{2}\ge \frac{3}{4}{\ \Leftrightarrow \ cos 2\pi t\ }+1\ge \frac{3}{2}{\ \Leftrightarrow \ cos 2\pi t\ }\ge \frac{1}{2} .\)
Решим неравенство, построив график функции \(y={\ cos 2\pi t\ }\) при \(t\in [ 0;1].\)
Найдем, при каких значениях t выполняется условие: \(\displaystyle cos 2 \pi t = \frac{1}{2}\)
\(\displaystyle cos 2 \pi t = \frac{1}{2} \Leftrightarrow 2 \pi t = \pm \frac{\pi}{3} = 2\pi k; k \in Z;\)
\(\displaystyle t=\pm \frac{1}{6}+k; k \in Z \)
На отрезке [0;1] лежат корни этого уравнения: \(t=\frac{1}{6}\) и \(t=\frac{5}{6}.\) Мы отметили эти точки на графике.
Неравенство выполняется, если \(\displaystyle 0 \leq t \leq \frac{1}{6}\) или \(\displaystyle \frac{5}{6} \leq t \leq 1.\)
Решения неравенства образуют два отрезка, длина каждого из них равна \(\displaystyle \frac{1}{6};\)
\(\displaystyle \frac{1}{6}+\frac{1}{6}=\frac{2}{6}=\frac{1}{3} \approx 0,33\)
Ответ: 0,33
9. Анна Малкова
В ожидании Нового Года Дед-Мороз и Санта Клаус затеяли гонки по круговой орбите вокруг Земли. Длина окружности, по которой они летают, составляет 33 тыс. км.
Первым стартует (на оленях) Санта Клаус. Через 30 часов из той же точки следом за ним вылетает (на тройке лошадей) Дед-Мороз. Через 10 часов после старта он в первый раз догоняет Санта Клауса, а еще через 44 часа догоняет во второй раз. Найдите скорость Деда Мороза. Ответ выразите в км/ч.
Решение:
Пусть скорость Санта Клауса равна х км/ч, а скорость Деда Мороза у км/ч.
Составим уравнение для момента встречи.
Дед Мороз был в пути 10 часов и пролетел то же расстояние, что и Санта Клаус за 40 часов.
\(10y=40x\), получим \(y=4x\)
Через 44 часа Дед Мороз снова догнал Санта Клауса. Это значит, что расстояние, которое за это время преодолел Дед Мороз, на 1 круг, то есть на 33 тысячи километров больше расстояния, которое пролетел Санта.
\(44y-44x=33000\)
\(4y-4x=3000\)
\(4\cdot 4x-4x=3000\)
\(12x=3000\)
\(x=250\) км/ч – скорость Санта Клауса, \(250\cdot 4=1000\) км/ч – скорость Деда мороза
Ответ: 1000
10. Анна Малкова
Графики функций \(y=\left|x-a\right|+c\) и \(y=kx+b\) пересекаются в точках A и B. Найдите ординату точки B.
Решение:
На рисунке изображены графики двух функций.
Обозначим \(f(x)=\ \left|x-a\right|+c,\ \ g(x)=kx+b.\)
По условию, графики этих функций пересекаются в точках A и B, причем точка B находится за пределами рисунка. Нужно найти ординату точки B. Для этого «расшифруем» формулы обеих функций.
График функции \(f(x)\) получен из графика функции \(\left|x-a\right|\) сдвигом на а единиц вправо (при а \(\textgreater \) 0) на c по вертикали. В нашем случае с \(\textless \)0, так как график сдвинут вниз.
Вершина графика функции \(f(x)\) имеет абсциссу 3 и ординату -4. Это значит, что \(a=3,\ c=-4.\)
Получили: \(f(x)=\left|x-3\right|-4.\)
Функция \(g(x)\ \) – линейная, ее график – прямая.
\(g(0)=5,\ \) это означает, что \(b=5.\ \)
Найдем угловой коэффициент \(k\) этой прямой как тангенс угла ее наклона к положительному направлению оси Х.
Получим, что \(\displaystyle g(x)=\frac{1}{2}x+5.\)
Найдем координаты точек пересечения графиков \(f(x)=\left|x-3\right|-4\) и \(\displaystyle g(x)=\frac{1}{2}x+5.\) Решим уравнение:
\(\displaystyle \left|x-3\right|-4=\frac{1}{2}x+5\)
При этом \(x\textgreater 3,\) так как точка B лежит на правой ветви графика модуля, то есть правее правее прямой \(x=3.\)
Раскроем модуль. При \(x\textgreater 3\\) получим, что \(x-3\textgreater 0.\)
\(\displaystyle x-3-4=\frac{1}{2}x+5;\ 2x-14=x+10;\ x=24.\)
Чтобы найти ординату точки B, подставим значение \(x=24\) в уравнение правой ветви модуля \(y=x-7.\)
\(y(24)=x-7=17\)
Ответ: 17
11. ФИПИ
Найдите наименьшее значение функции \(y=-17-6,5\pi +26x-26\sqrt{2}{sin x\ \ }\) на отрезке \(\displaystyle [ 0;\frac{\pi }{2}].\)
Решение.
Наименьшее значение функции на отрезке может достигаться либо в точке минимума, либо в конце отрезка.
Чтобы найти точку минимума, возьмем производную функции y(х).
\(y'(x)={(-17-6,5\pi +26x-26\sqrt{2}{sin x\ })}'=26-26\sqrt{2}{cos x\ }.\)
\(y'=0;\ 26-26\sqrt{2}{cos x\ }=0;\ \ \)
\(\displaystyle {cos x\ }=\frac{1}{\sqrt{2}}\ .\) На отрезке \(\displaystyle [ 0;\frac{\pi }{2}]\) это уравнение имеет единственное решение
\(\displaystyle x=\frac{\pi }{4}.\)
Найдем знаки производной на отрезке \(\displaystyle [ 0;\frac{\pi }{2}].\)
Для проверки возьмем точки 0 и \(\displaystyle \frac{\pi }{2}.\)
\({cos 0=1,\ }\) тогда \(y'=26-26\sqrt{2}\textless 0;\)
\(\displaystyle {cos \frac{\pi }{2}=0\ }\) тогда \(y'=26\textgreater 0.\)
Значит, если \(\displaystyle x\textless \frac{\pi }{4},\) то \(y'\textless 0;\) если \(x\textgreater \frac{\pi }{4}\) , то \(y'\textgreater 0\)
При переходе через точку \(\displaystyle x=\frac{\pi }{4}\) производная меняет знак с «минуса» на «плюс», а это означает, что \(\displaystyle x=\frac{\pi }{4}\) - точка минимума функции, единственная на данном отрезке.
Тогда \(\displaystyle {\ \ y}_{min}=y(\frac{\pi }{4})=-17-6,5\pi +26 \cdot \frac{\pi }{4}-26\sqrt{2}{sin \frac{\pi }{4}=\ \ }\)
\(=-17-6,5\pi +26\cdot \frac{\pi }{4}-26\sqrt{2}\cdot \frac{\sqrt{2}}{2}=-17-26=-43\)
Ответ: - 43
Часть 2. Задания с развернутым ответом
12. Анна Малкова
а) Решите уравнение
\(\left ( \frac{{cos}^2 x}{2}+sin x+1 \right ) \sqrt{16-x^2}=0\)
б) Найдите все корни уравнения на отрезке \([ -4;0].\)
Решение:
\(\displaystyle \left (\frac{{{cos}^2 x\ }}{2}+{sin x\ }+1\right )\sqrt{16-x^2}=0\)
Произведение двух множителей равно нулю, тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл.
Поэтому уравнение равносильно системе:
Из основного тригонометрического тождества: \({{cos}^2 x\ }={{1-sin}^2 x\ }\)
Решим уравнение:
\(\displaystyle \frac{{{1-sin}^2 x\ }}{2}+{sin x\ }+1=0\Leftrightarrow -{{sin}^2 x\ }+2{sin x\ }+3=0\)
Замена: \({sin x=t;\ \ \left|t\right|\le 1;\ }\)
Вернемся к переменной x:
Уравнение \({sin x\ }=3\) решений не имеет, т.к. \({|sin x|\ }\le 1.\)
\(\displaystyle {sin x\ }=-1 \Leftrightarrow x=-\frac{\pi }{2}+2\pi k;k\in Z.\)
Система примет вид:
Решив второе неравенство методом интервалов, получим:
\(-4\le x\le 4\)
Сделаем отбор решений с помощью числовой прямой. Отметим на ней отрезок [-4; 4] и точки из серии решений \(\displaystyle x=-\frac{\pi }{2}+2\pi k;k\in Z.\)
Если k=0, \(\displaystyle x=-\frac{\pi }{2},\) то \(\displaystyle -4\le -\frac{\pi }{2}\le 4,\) подходит.
Если \(k=1,\) то \(\displaystyle \ x=-\frac{\pi }{2}+2\pi =\frac{3\pi }{2}\ .\)
Сравним \(\displaystyle \frac{3\pi }{2}\vee 4.\ \)
\(3\pi \vee 8\)
Так как \(\pi \textgreater 3,\ \ 3\pi \textgreater 8.\)
Это означает, что \(\displaystyle x=\frac{3\pi }{2}\) не входит в отрезок \([ -4;4].\)
Если \(k\ge \)1 , то \(\displaystyle x=-\frac{\pi }{2}+2\pi k\ \Leftrightarrow \) \(\displaystyle x\ge \frac{3\pi }{2}\textgreater 4\) не входит в отрезок \([ -4;4],\)
Если \(k\le -1\) то \(\displaystyle x\le -\frac{5\pi }{2}\textless -4\) не входит в отрезок \([ -4;4],\)
получили, что \(\displaystyle x=-\frac{\pi }{2}\) или \(x=-4\) или \(x=4.\)
б) Этот пункт решения очень простой. Среди найденных решений надо выбрать отрицательные. Это \(\displaystyle -4;\ -\ \frac{\pi }{2}.\)
Ответ: а) \(\displaystyle -4;\ -\ \ \frac{\pi }{2}:\ 4\ \ \) б) \(\displaystyle \ -4;\ -\ \frac{\pi }{2}.\)
13. Анна Малкова Отрезки AB и CD - диаметры верхнего и нижнего оснований цилиндра соответственно. Треугольники ABС и ABD равнобедренные (AB – основание).
а) Докажите, что AB перпендикулярен CD.
б) Найдите объем пирамиды ABCD, если AB = 8, AC = 13.
Решение:
а) \(\triangle ABC\) и \(\triangle ABD\) равнобедренные с основанием AB. Докажем, что AB перпендикулярен CD.
Пусть \(O_1\) - центр верхнего основания,
\(O\) - центр нижнего основания.
\(O_1\) - середина \(AB,\) тогда \({CO}_1\) и \(DO_1\) - медианы треугольников \(ABC\) и \(ABD.\)
т.к. \(\triangle ABC\) и \(\triangle ABD\) равнобедренные,
\(\ \ CO_1\bot AB;\ \ DO_1\bot AB.\)
\(\left. \begin{array}{c}
CO_1\bot AB \\
DO_1\bot AB \\
CO_1\cap DO_1 \end{array}
\right\}\Rightarrow (CO_1D)\bot AB\) по признаку перпендикулярности прямой и плоскости.
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой лежащей в этой плоскости.
\(\left. \begin{array}{c}
(CO_1D)\bot AB \\
CD\in (CO_1D) \\
\ \end{array}
\right\}\Rightarrow CD\bot AB\) по определению перпендикулярности прямой и плоскости.
б) \(AB=8;\ \ AC=13.\) Найдем \(V_{ABCD}.\)
\(\triangle ABC\) и \(\triangle ABD\) равнобедренные,
\(CD\bot AB.\)
Докажем, что \(AC=BC=AD=BD.\)
\(OO_1\) - ось цилиндра,
\(\triangle CO_1D\) - равнобедренный, т.к.\(\ OO_1\) - его высота и медиана \(\Rightarrow {CO}_1=\ DO_1.\)
\(\triangle O_1AD=\triangle O_1AC\) по двум катетам (прямоугольные, \(O_1A\) - общий катет, \({CO}_1\ =\ DO_1\))\(\ \Rightarrow AD=AC.\)
\(\triangle ABC\) и \(\triangle ABD\) – равнобедренные, поэтому \(AC=BC\) и \(AD\ =BD.\)
Получили \(AC=BC=AD=BD.\)
Сделаем чертеж пирамиды \(CABD,\) у которой
\(AC=BC=AD=BD.\)
\(\displaystyle S_{\triangle ABD}=\frac{1}{2}AB\cdot DO_1,\)
\(\triangle DO_1B\)- прямоугольный,
Из \(\triangle DO_1B:\ \ DO_1=\sqrt{{BD}^2-{BO_1}^2}=\)
\(=\sqrt{169-16}=\sqrt{153}=3\sqrt{17}\)
\(S_{\triangle ABD}=4\cdot 3\sqrt{17}=12\sqrt{17}\)
В плоскости \(CO_1D\ \)проведем \(CH\bot \ DO_1.\)
\(\left. \begin{array}{c}
CH\bot \ DO_1 \\
(CO_1D\ \ )\ \bot AB\Rightarrow CH\bot AB \end{array}
\right\}\Rightarrow CH\bot (ABD)\) по признаку перпендикулярности прямой и плоскости
\(CH\) - высота пирамиды
\(\triangle CO_1D\) - равнобедренный (см. пункт а) \(O_1\ C=\ DO_1=3\sqrt{17}\ ;\ \ \ \ CD=8\)
\(OO_1\) - высота и медиана \(\triangle CO_1D\)
\(OO_1=\sqrt{{DO_1}^2-{DO}^2}=\sqrt{153-16}=\sqrt{137}\)
\(\displaystyle S_{\triangle CO_1D}=\frac{1}{2}CD\cdot OO_1=\frac{1}{2}DO_1\cdot CH\Rightarrow CH=\)
\(\displaystyle =\frac{CD\cdot OO_1}{DO_1}=\frac{8\cdot \sqrt{137}}{3\sqrt{17}}\)
\(\displaystyle V_{ABCD}=\frac{1}{3}S_{ABD}\cdot CH=\frac{1}{3}\cdot 12\sqrt{17\cdot }\frac{8\cdot \sqrt{137}}{3\sqrt{17}}=\frac{32\sqrt{137}}{3}\)
Второй способ:
\(\displaystyle V_{ABCD}=2V_{ABCO}=\frac{2}{3}S_{\triangle ABO}\cdot h\)
\(\displaystyle S_{\triangle ABO}=\frac{1}{2}AB\cdot OO_1\)
\(OO_1\) - высота и медиана \(\triangle CO_1D\)
\(OO_1=\sqrt{{DO_1}^2-{DO}^2}=\sqrt{153-16}=\sqrt{137}\)
\(\displaystyle S_{\triangle ABO}=\frac{1}{2}AB\cdot OO_1=\frac{1}{2}\cdot 8\cdot \sqrt{137}=4\sqrt{137}\)
\(\displaystyle V_{ABCD}=\frac{2}{3}\cdot 4\sqrt{137}\cdot 4=\frac{32\sqrt{137}}{3}.\)
Ответ: \(\displaystyle V_{ABCD}=\frac{32\sqrt{137}}{3}\)
14. ФИПИ
Решите неравенство: \(\displaystyle {{log}_7 (2+\frac{2}{x})\ }-{{log}_7 (x+3)\ }\le {{log}_7 \frac{(6+x)}{x^2}\ }\)
Решение:
\(\displaystyle {{log}_7 (2+\frac{2}{x})\ }-{{log}_7 (x+3)\ }\le {{log}_7 \frac{(6+x)}{x^2}\Leftrightarrow \ \ }\)
Запишем в одной системе ОДЗ и само неравенство, в котором
разность логарифмов заменим на логарифм частного.
\(\displaystyle \Leftrightarrow \left\{ \begin{array}{c}
2+\frac{2}{x}\textgreater 0 \\
x+3\textgreater 0 \\
\frac{(6+x)}{x^2}\textgreater 0 \\
{{log}_7 \frac{(2+\frac{2}{x})}{(x+3)}\ }\le {{log}_7 \frac{(6+x)}{x^2}\ } \end{array}
\Leftrightarrow \ \right.\)
\(\displaystyle \Leftrightarrow \left\{ \begin{array}{c}
\frac{x+1}{x}\textgreater 0 \\
x+3\textgreater 0 \\
\frac{(6+x)}{x^2}\textgreater 0 \\
{{log}_7 \frac{2x+2}{x(x+3)}\ }\le {{log}_7 \frac{(6+x)}{x^2}\ } \end{array}
\Leftrightarrow \right.\)
Функция \(y={{log}_7 t\ }\) монотонно возрастает, поэтому, если
\({{log}_7 t_1\ }\le {{log}_7 t_2\ },\) то \(t_1\le t_2\) при \(t_1\textgreater 0;\ \ t_2\textgreater 0.\) Получим:
\(\displaystyle \left\{ \begin{array}{c}
\frac{x+1}{x}\textgreater 0 \\
x+3\textgreater 0 \\
\frac{6+x}{x^2}\textgreater 0 \\
\frac{2x+2}{x(x+3)}\le \frac{(6+x)}{x^2} \end{array}
\right.\)
Неравенство \(\displaystyle \frac{6+x}{x^2}\textgreater 0\) верно при всех \(x,\ \) удовлетворяющих первым двум неравенствам.
В последнем неравенстве перенесем все в левую часть и приведем к общему знаменателю. Получим:
\(\displaystyle \left\{ \begin{array}{c}
\frac{x+1}{x}\textgreater 0 \\
x+3\textgreater 0 \\
\frac{2x^2+2x-(6+x)(x+3)}{x^2(x+3)}\le 0 \end{array}
\Leftrightarrow \left\{ \begin{array}{c}
\frac{x+1}{x}\textgreater 0 \\
x+3\textgreater 0 \\
\frac{2x^2+2x-x^2-9x-18}{x^2}\le 0 \end{array}
\Leftrightarrow \right.\right.\)
В последнем неравенстве мы домножили обе части на положительное выражение х+3.
\(\left\{ \begin{array}{c}
\frac{x+1}{x}\textgreater 0 \\
x\textgreater -3 \\
\frac{x^2-7x-18}{x^2}\le 0 \end{array}
\Leftrightarrow \right.\left\{ \begin{array}{c}
\frac{x+1}{x}\textgreater 0 \\
x\textgreater -3 \\
\frac{(x+2)(x-9)}{x^2}\le 0 \end{array}
\Leftrightarrow \right.\)
Решим первое и третье неравенства системы методом интервалов и отметим решения всех неравенств на одной прямой.
Получим: \(\ x\in [-2;-1)\cup (0;9]\)
Ответ: \([-2;-1)\cup (0;9]\)
15. Анна Малкова
Задумав разбогатеть, 10 декабря Валентина Петровна отправилась в банк и взяла в кредит 230 тысяч рублей на 49 месяцев. Условия возврата кредита следующие:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 9-е число каждого месяца необходимо выплатить часть долга;
– 10-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 10-е число предыдущего месяца.
Полученные деньги Валентина Петровна планирует в тот же день дать в кредит студенту Василию (испытывающему финансовые затруднения), а условия собирается поставить следующие:
- 10 декабря каждого следующего года долг увеличивается на 30%, после чего Василий передает Валентине Петровне очередной платеж.
- Кредит выплачивается двумя равными ежегодными платежами.
Какой будет прибыль Валентины Петровны, если студент Василий согласится на ее условия? Ответ выразите в тысячах рублей.
Решение:
Первый кредит (который Валентина Петровна берет в банке) – это кредит с дифференцированными платежами. Здесь есть информация о сумме долга, причем сумма долга уменьшается равномерно.
Пусть
S=230 тыс. рублей – сумма кредита.
n=49 месяцев
r=2% - процент банка
Воспользуемся формулой для величины переплаты по кредиту:
\(\displaystyle \prod =\frac{n+1}{2}\cdot \frac{r}{100}\cdot S=\frac{25\cdot 2}{100}\cdot 230=115\) тыс. рублей.
Напомним, что на экзамене эту формулу надо вывести, чтобы получить за задачу полный балл.
Общая сумма выплат: \(B=S+\prod =230+115=345\ \\) тыс. рублей
Второй кредит (который Валентина Петровна намерена открыть для студента Василия) – аннуитет.
Составим схему погашения второго кредита.
S = 230 тыс. рублей – сумма кредита, на 2года
р = 30 % - процент банка
\(\displaystyle k=(1+\frac{p}{100})=1,3\) – коэффициент, показывающий, во сколько раз увеличивается сумма долга после начисления процентов,
X – ежегодный платеж
Схема погашения кредита:
| Долг после начисления % | Выплата | Остаток долга | |
| 1 год | \(Sk\) | \(X\) | \(Sk-X\) |
| 2 год | \((Sk-X)k\) | \(X\) | \((Sk-X)k-X\) |
\((Sk-X)k-X=0\Leftrightarrow Sk^2-X(k+1)=0\Leftrightarrow \)
\(\displaystyle X=\frac{Sk^2}{k+1}=\frac{230\cdot 1,69}{2,3}=169\) тыс. руб.
Всего Василий должен выплатить Валентине Петровне \(2X=2\cdot 169=338\) тыс. руб. В результате Валентина Петровна отдаст 345 тыс. рублей, чтобы погасить кредит банка, а получит от Василия 338 тыс. рублей.
Ее прибыль отрицательна и составляет \(338-345\ =\ -7\) тыс. рублей. Другими словами, Валентина Петровна потеряет 7 тысяч рублей.
Ответ:\(\ -7\) (тысяч рублей)
16. Анна Малкова Боковая сторона AB трапеции ABCD перпендикулярна основаниям AD и BС. Из точки М, лежащей на стороне AB, опущен перпендикуляр МР на противоположную боковую сторону.
а) Докажите, что точки М, B, С и Р лежат на одной окружности.
б) Найдите площадь трапеции ABCD, если радиус вписанной в нее окружности равен 6,а отношение AР : DM = 3 : 5.
Решение:
а) В четырехугольнике МBСР углы B и Р - прямые, их сумма равна 180 градусов. Следовательно, точки М, B, С и Р лежат на одной окружности. Мы сделали пункт (а) за 30 секунд!
б) Окружность можно описать не только вокруг четырёхугольника \(MBCP,\) но и вокруг четырехугольника \(AMPD.\) Сумма углов MAD и DPМ равна 180 градусов, так как эти углы прямые.
Найдем на рисунке подобные треугольники. Они неочевидны. И все-таки они есть!
\(\angle MBP=\angle MCP\) (опираются на дугу \(MP\) верхней окружности).
\(\angle MAP=\angle MDP\) (опираются на дугу \(MP\) нижней окружности).
\(\vartriangle ABP\sim \vartriangle DCM\) по двум углам. Запишем соотношение их сходственных сторон:
\(\displaystyle \frac{AP}{DM}=\frac{AB}{CD}=\frac{3}{5}\) (по условию). С другой стороны, \(\frac{AB}{CD}=sin\angle ADC;\) \(sin\angle ADC=\frac{3}{5}.\ \)
Если в трапецию \(ABCD\) вписана окружность, то высота трапеции равна диаметру этой окружности. Поэтому \(AB=2r=12,\) и тогдa \(\displaystyle \ \ CD=AB\cdot \frac{5}{3}=20.\)
Трапеция \(ABCD\) описана вокруг окружности, и суммы длин ее противоположных сторон равны: \(AB+CD=AD+BC=\ 32.\ \) Найдем площадь трапеции:
Ответ: 192.
17. Анна Малкова
Дана система неравенств:
\(\left\{ \begin{array}{c}
9-y\le 2^{k+1} \\
y\le 9-2^k-\left|x\right| \\
4^k-5\cdot 2^k+4\le 0 \end{array}
\right.\)
а) Изобразите ее решение в координатах (x; у) при целых значениях k.
б) Найдите площадь полученной фигуры.
Решение:
Рассмотрим третье неравенство системы:
\(4^k-5\cdot 2^k+4\le 0\)
Замена: \(2^k=t,\ t\textgreater 0,\) тогда
\(t^2-5t+4\le 0\)
\((t-1)(t-4)\le 0\)
\(1\le t\le 4\)
\(1\le 2^k\le 4\)
\(2^0\le 2^k\le 2^2\)
\(0\le k\le 2,\ k\in Z\)
Вернемся к системе:
\(\left\{ \begin{array}{c}
9-2^{k+1}\le y\le 9-2^k-\left|x\right| \\
0\le k\le 2,\ k\in Z \end{array}
\right.\)
Решим данную систему графически.
Если k = 2, то
\(9-8\le y\le 9-4-\left|x\right|\)
\(1\le y\le 5-\left|x\right|\)
Если k = 1, то
\(9-4\le y\le 9-2-\left|x\right|\)
\(5\le y\le 7-\left|x\right|\)
Если k = 0, то
\(9-2\le y\le 9-1-\left|x\right|\)
\(7\le y\le 8-\left|x\right|\)
Получим:
18. ФИПИ
За новогодним столом дети ели бутерброды и конфеты, причем каждый что-то ел, и может быть так, что кто-то ел и то и другое. Известно, что мальчиков, евших бутерброды, было не более чем 5/16 от общего числа детей, евших бутерброды, а мальчиков, евших конфеты, было не более 2/5 от общего числа детей, евших конфеты.
а) Могло ли за столом быть 13 мальчиков, если дополнительно известно, что всего за столом было 25 детей?
б) Какое наибольшее количество мальчиков могло быть за столом, если дополнительно известно, что всего за столом было 25 детей?
в) Какую наименьшую долю могли составлять девочки от общего числа детей без дополнительного условия пунктов а и б?
Решение:
Сделаем «заготовку» для всех пунктов задачи.
Введем переменные, обозначающие количество мальчиков с бутербродами, мальчиков с конфетами, девочек с бутербродами, девочек с конфетами, всего мальчиков и всего девочек.
| Бутерброды | Конфеты | Всего | |
| Мальчики | \(m_1\) | \(m_2\) | \(m\) |
| Девочки | \(d_1\) | \(d_2\) | \(d\) |
Известно, что мальчиков, евших бутерброды, было не более чем 5/16 от общего числа детей, евших бутерброды, т.е. \(\displaystyle m_1\le \frac{5}{16}(m_1+d_1).\)
Мальчиков, евших конфеты, было не более 2/5 от общего числа детей, евших конфеты, т.е. \(\displaystyle m_2\le \frac{2}{5}(m_2+d_2).\)
Получили систему двух неравенств с четырьмя переменными. Преобразуем её:
\(\displaystyle \left\{ \begin{array}{c}
m_1\le \frac{5}{16}(m_1+d_1) \\
m_2\le \frac{2}{5}(m_2+d_2) \end{array}
\right.\Leftrightarrow \left\{ \begin{array}{c}
11m_1\le 5d_1 \\
3m_2\le 2d_2 \end{array}
\right.\Leftrightarrow \left\{ \begin{array}{c}
33m_1\le 15d_1 \\
33m_2\le 22d_2 \end{array}
\right.\)
Сложив неравенства, получим: \(33(m_1+m_2)\le 15d_1+22d_2\)
У нас появилось условие, которое связывает следующие переменные: количество мальчиков с бутербродами и мальчиков с конфетами; девочек с бутербродами и девочек с конфетами. Но нас спрашивают про общее количество мальчиков и общее количество девочек.
Заметим, что мальчик может есть и бутерброды, и конфеты, и девочка тоже.
Поэтому, если мы сложим \(m_1\) и \(m_2,\) то получим величину, которая больше или равна количества всех мальчиков.
Сложив \(d_1\) и \(d_2\) , получим величину, которая не меньше количества всех девочек.
Получили дополнительные условия:
\(m_1+m_2\ge m,\)
\(d_1+d_2\ge d. \)
Тогда
\(33m\le 33(m_1+m_2)\)
Кроме того, \(d_1\le d\) и \(d_2\le d\) (не все девочки могли есть бутерброды, и не все девочки могли есть конфеты).
Тогда \(\left\{ \begin{array}{c}
{15d}_1\le 15d \\
22d_2\le 22d \end{array}
\Rightarrow \right.15d_1+22d_2\le 37d\)
Получим: \(33m\le 33(m_1+m_2)\le 15d_1+22d_2 \leq 37d \Rightarrow 33m\leq 37d\), следовательно \(33m\le 37d.\) Это условие для количества мальчиков и количества девочек за столом. Остается подставлять в него по очереди, один за другим, данные пунктов (а), (б) и (в).
а) Предположим, что \(m=13;\ \ d=12;\ \ \ \) \(m+d=25.\)
\(33\cdot 13\textless 37\cdot 12,\ \) неравенство \(33m \leq 37d \) выполняется.
Возьмем \(m_1=5;\ \ m_2=8;\ d_1=d_2=12\ \ \)
Проверим выполнение условий \(
\left\{\begin{matrix}
11m_1 \leq 5d_1\\ 3m_2 \leq 2d_2
\end{matrix}\right. \), получим \(
\left\{\begin{matrix}
55\leq 60\\ 24 \leq 24
\end{matrix}\right.
\) – все условия выполнены.
Ответ в пункте (а): Да, может. Вот пример: \(m_1=5;\ \ m_2=8;\ d_1=d_2=12.\ \)
б) Если\(\ m\) – количество мальчиков, то \(d=25-\ m\) количество девочек.
Подставим в неравенство \(33m\le 37d.\)
\(\displaystyle 33m\le 37(25-m)\Rightarrow 33m+37m\le 37\cdot 25\Rightarrow m\le \frac{37\cdot 25}{70}\Rightarrow m\le 13\frac{3}{14}\)
Значит, \(m\le 13.\) Это оценка. Пример для \(m=13\) приведен в пункте (а).
в) Пусть \(p\) – доля девочек среди всех детей.
\(\displaystyle p=\frac{d}{m+d}\) Найдем \(p_{min}.\)
\(\displaystyle 33m\le 37d\Rightarrow \frac{m}{d}\le \frac{37}{33}\) . Прибавим 1 к обеим частям неравенства.
\(\displaystyle \frac{m}{d}+1\le \frac{37}{33}+1\Rightarrow \frac{m+d}{d}\le \frac{70}{33}\Rightarrow \frac{d}{m+d}\ge \frac{33}{70}\) . Это оценка.
Приведем пример для \(\displaystyle p=\frac{33}{70}.\)
Пусть за столом 33 девочки и 37 мальчиков, причем девочки едят всё, то есть \(d_1=d_2\) =33.
По условию,
\(\left\{ \begin{array}{c}
11m_1\le 5d_1\ \ \ \ \ \ \ \ \ \\
3m_2\le 2d_2 \end{array}
\right.\)
\(\left\{ \begin{array}{c}
11m_1\le 5\cdot 33 \\
3m_2\le 2\cdot 33 \end{array}
\right.\ \ \ \ \ \)
\(\left\{ \begin{array}{c}
m_1\le 15 \\
m_2\le 22 \end{array}
\right..\)
Возьмем \(m_1=15,\) \(m_2=22,\) тогда \(m_1+m_2=37,\) все условия выполнены. Наименьшая доля девочек при этом равна \(\displaystyle \frac{33}{70}.\)
Ответ: \(\displaystyle \frac{33}{70}\)
